Fórum: Trigonometria

[1] [2] [3]

Szeretnél hozzászólni? Jelentkezz be.

2006-09-24 20:21:53

Becsülöm a humorodat! ;-) Valamelyik országban nem kizárt, de Én akkor mint kezdőtanár (Erdélyben) az ilyesmit az érvényben levő tantervek szerint a 9-10. osztályos trigonometria tantárgy keretében tanítottam. Egyébként a szóbanforgó könyv címe idegen nyelvről lefordítva kb így hangzik : " A régi trigonomertia varázsa" :-) A bizonyításod nyomán, most már csak azon törnöm a fejem, hogy a (0,2) intervallumból pl. milyen értékeket NEM vesz fel a jelzett tört! Mert az 1 érték nagyon gyanus!

[13] Lóczi Lajos	2006-09-24 20:07:15
Lehet, hogy 1983-ban még tanítottak analízist 9-10.-ben :)
Előzmény: [12] epsilon, 2006-09-24 19:29:32

[12] epsilon	2006-09-24 19:29:32
Kedves Lajos! Kösz szépen, szép elegáns bizonyítás. A feladat egy 9.-10. osztályos könyvben találtam, ezért szeretnék rá olyan bizonyítást találni, ami nem használ (esetleg álcázottan sem) matematikai analízist!

[11] Lóczi Lajos

2006-09-23 17:58:06

Szélsőértékszámítással a feladat teljesen standard.

Állítás: A 0 $\le$ $\alpha$ , 0 $\le$ $\beta$ , $\alpha$ + $\beta$ $\le$ $\pi$ háromszöglapon az

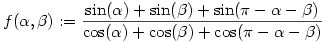
$f(\alpha,\beta):=\frac{\sin(\alpha)+\sin(\beta)+\sin(\pi-\alpha-\beta)}{\cos(\alpha)+\cos(\beta)+\cos(\pi-\alpha-\beta)}$

függvény értékkészlete a [0,2] intervallum, továbbá a paramétertartomány belsejében az értékkészlet a (0,2) nyílt intervallum.

Bizonyítás: Elemi számolás mutatja, hogy az $\alpha$ , $\beta$ paraméterekre kirótt megkötések mellett az f függvény parciális deriváltjai csak ott lehetnek nullák, ahol $\alpha$ = $\pi$ /3 vagy $\alpha$ = $\pi$ vagy $\beta$ = $\pi$ /3 vagy $\beta$ = $\pi$ vagy $\alpha$ + $\beta$ /2= $\pi$ /2 vagy $\alpha$ + $\beta$ /2=3 $\pi$ /2. Ezek tehát a lehetséges szélsőértékhelyek a paraméterháromszög belsejében és határán. (A teljes határt amúgy is külön meg kell még vizsgálni.) Ezeket az értékeket az f függvénybe helyettesítve az alábbi triviális egyváltozós szélsőértékfeladatokat kapjuk (a szimmetria miatt a többi kimaradó eset csak betűcsere):

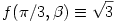
$f(\pi/3,\beta) \equiv \sqrt{3}$

f(0, $\beta$ ) $\equiv$ f( $\pi$ - $\beta$ , $\beta$ ) $\equiv$ 2sin ( $\beta$ )

f( $\pi$ , $\beta$ ) $\equiv$ 0

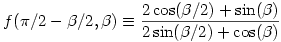
$f(\pi/2-\beta/2,\beta) \equiv \frac{2\cos(\beta/2)+\sin(\beta)}{2\sin(\beta/2)+\cos(\beta)}$

Itt csak az utolsó eset szorul némi magyarázatra: mivel az utolsó képlet deriváltja

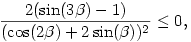
$\frac{2 (\sin (3 \beta )-1)}{(\cos (2 \beta )+2 \sin (\beta ))^2}\le 0,$

ezért ez a függvény monoton fogyó 0 $\le$ $\beta$ $\le$ $\pi$ esetén, a határpontokban az értéke 2 és 0. Az állítást beláttuk.

Előzmény: [6] epsilon, 2006-09-22 05:54:52

[10] epsilon

2006-09-22 16:55:13

Kösz a tippet, de valóban háromszög szögeiről van szó a MathTypel írtam, és hamarjában a kis delta került elő. Néhény érdekes eredmény: ha jól számoltam, szabályos háromszög esetén már a tört értéke >1 akárcsk egy 45°, 45°, 90°-os szögekkel rendelkező 3-szög esetén, de már egy 30°, 30°, 120° nagyságú szögek esetén a tört <1. Szóval valójában nem sejtem, hogy hol "fordulhat meg a helyzet" az 1 esetében? :-(

[9] lorantfy	2006-09-22 12:23:18
Biztos, hogy egy háromszög belső szögeiről van szó? Mert akkor a 3. szög gamma szokott lenni, vagy Te írtad véletlemnül deltának?
Előzmény: [8] epsilon, 2006-09-22 12:16:10

[8] epsilon

2006-09-22 12:16:10

Helló! Igen, többféle trigóképlettel próbálkoztam, de nagyon ellentmondásosnak tűntek a korlátok, és nem jutottam dűlőre, hogy mi mikor igaz, mert az ellenkezője is bejött. Végül is azt mind vadászom, hogy a szóbanforgó törtnek melyek a legjobb alsó illetve felső korlátai. A könyvben (1983-ból származik), csak halomban felsorolnak összefüggéseket amik egy 3-szögben fennálnak, de már kaptam más hibás feladatot is, sikerült kijavítanom, ezzel még nem jutottam dűlőre :-(

[7] nadorp

2006-09-22 10:20:27

Szia !

Nem jó az alsó határ, mert pld.

$\frac{\sin1^\circ+\sin1^\circ+\sin178^\circ}{\cos1^\circ+\cos1^\circ+\cos178^\circ}=0,069783056219622<1$

Nem hegyesszőgű háromszög kell, hogy legyen?

Előzmény: [6] epsilon, 2006-09-22 05:54:52

[6] epsilon	2006-09-22 05:54:52
Helló! Egy régi könyvből előkerült a következő feladat. Igazoljuk, hogy bármely háromszögben fennáll az alábbi dupla egyenlőtlenség. Miért nem állhat fenn egyenlőség? Valami jó ötlet egsyerű bizonyításra?

[5] epsilon	2006-06-10 10:02:43
Köszi! Ezek nem igazán trigonomertia történeti infók, de valóban, a Googlebe beírva "history of trigonometry" csodálatos rendszerezett átfogó trigonometriai történeti linkeket találtam, ismételten kösz! ;-)

[4] lgdt	2006-06-10 04:43:25
érdekességként: http://en.wikipedia.org/wiki/Rational_trigonometry

[3] epsilon	2006-06-01 21:31:41
Kedves Lóczi Lajos! Kösz szépen, valóban, angolul szép találatok vannak! Magyarul szerettem volna, de így marad, hogy lefordítsam.

[2] Lóczi Lajos	2006-06-01 20:23:21
Leggyorsabb, ha egy keresőprogrammal rákeresel az interneten a "history of trigonometry"-re; én már az első találati oldal listájában bőven találtam szép összefoglalókat a témáról.
Előzmény: [1] epsilon, 2006-06-01 19:00:10

[1] epsilon

2006-06-01 19:00:10

Mindenkit tistelettel üdvözlök!

Nem tudom, jó helyen nyitottam-e ezt a tipicot, hogy illik-e a fórumon segélykérést fölvetni, stb., de az illetékesek eldöntik.

Egyetlen kérdésem lenne: tud-e valaki olyan könyvcímeket, és főként netes információforrást, ahol "A trigonometria története" címszó alá információkat lehetne gyűjteni?

Tisztelettel üdv: epsilon

[1] [2] [3]

Már regisztráltál?
Új vendég vagy?