| [456] bily71 | 2009-11-14 07:57:05 |
 Először itt akartam leírni...
A Fremat-Wiles tétel egyoldalas(!) bizonyítása
Tétel: Az am+bm=cm egyenlőség m>2 esetén nem teljesül. (a,b,c,m N). N).
Bizonyítás: Minden Nnm:=(0m,1m,2m,...,nm) sorozat egy m-ed rendű számtani sorozat, ezt már beláttuk, és táblázatokkal demonstráltuk a [428]-ban, (n N). N).
Jelölje  m,i az Nnm sorozat különbségsorozatainak első tagjait, ekkor a megadható a következő általános(!) rekurzió, mely a binomiális együtthatókból állítja elő az Nnm sorozatot: m,i az Nnm sorozat különbségsorozatainak első tagjait, ekkor a megadható a következő általános(!) rekurzió, mely a binomiális együtthatókból állítja elő az Nnm sorozatot:
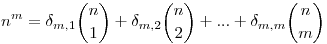 . .
A  m,i együtthatók hasonló háromszögbe rendezhetők, mint a binomiális együtthatók: m,i együtthatók hasonló háromszögbe rendezhetők, mint a binomiális együtthatók:
|
|
|
 1,1=1 1,1=1 |
|
|
|
|
|
 2,1=1 2,1=1 |
|
 2,2=2 2,2=2 |
|
|
|
 3,1=1 3,1=1 |
|
 3,2=6 3,2=6 |
|
 3,3=6 3,3=6 |
|
 4,1=1 4,1=1 |
|
 4,2=14 4,2=14 |
|
 4,3=36 4,3=36 |
|
 4,4=24 4,4=24 |
|
,
ahol a képzési szabály:  m,i=i[ m,i=i[ m-1,i-1+ m-1,i-1+ m-1,i], azaz, m-1,i], azaz,  m,i-t úgy kapjuk meg, összeadjuk a fölöttelévő két számot, majd megszorozzuk annyival, ahányadik tagot akarjuk kiszámolni a sorban. A sorok szélső tagjainál, ahol csak egy szám van egy másik fölött, ott értelemszerűen nullát adunk hozzá a fölső számhoz. m,i-t úgy kapjuk meg, összeadjuk a fölöttelévő két számot, majd megszorozzuk annyival, ahányadik tagot akarjuk kiszámolni a sorban. A sorok szélső tagjainál, ahol csak egy szám van egy másik fölött, ott értelemszerűen nullát adunk hozzá a fölső számhoz.  m,i megadható explicit formában is, de ez most nem fontos. m,i megadható explicit formában is, de ez most nem fontos.
A rekurziós alakból azonnal következik, hogy nm<(n+1)m-nm, ha m>2. Ez a bizonyítás legfontosabb összefüggése.
És most tételezzük fel indirekt módon, hogy az am+bm=cm egyenlőség teljesül minden m-re. Ebből az következik, hogy, mivel a,b,c egy m-ed rendű számtani sorozat tagjai,
bm=[(a+1)m-am]+[(a+2)m-(a+1)m]+...+[(c-1)m-(c-2)m]+[cm-(c-1)m].
Ami nem teljesülhet m>2 esetén, mert az egyenlőség jobb oldalán olyan összeg szerepel, melynek legalább egy tagja nagyobb bm-nél, hiszen, ha m>2, akkor nm<(n+1)m-nm, ebből következik, hogy
bm<(b+1)m-bm cm-(c-1)m. cm-(c-1)m.
Quod erat demonstrandum.
|
|
|
| [454] m2mm | 2009-11-01 20:09:16 |
 Hogy minden 2<páros előállna két prím összegeként... én nem érzem igaznak. Szerintem a Goldbach hamis, az ikerprím igaz. Lehet hogy egy "Könyv-konstrukciót" kéne keresni a Goldbach cáfolatára.
|
| Előzmény: [453] bily71, 2009-11-01 18:44:40 |
|
| [453] bily71 | 2009-11-01 18:44:40 |
 Mindig szerettem a bonyolult feladatokat, míg mások keresztrejtvényt fejtenek, én, régi gimis könyvekből, feladatok megoldásával ütöttem el az időt.
Kb. másfél éve tudom, hogy létezik egy sejtés, az ikerprím-sejtés, és, hogy 2300 év alatt, pedig volt egy-két zseni, senki nem tudta megválaszolni ezt az "egyszerű" kérdést.
Egyből megéreztem a kihívást, egy kérdésnek sincs ekkora presztízse a matematikában, aki választ ad rá, győzelmet arat minden matematikus felett, aki volt eddig a történelemben.
Nem hiszem, hogy ez pont nekem sikerülne, de szeretném egyszer látni a Könyv-bizonyítását ennek a sejtésnek, és szívesen részet vennék a kutatásban.
Az ilyen típusú sejtések, mint a Goldbach-, vagy a többi számelméleti sejtés, rendkívül egyszerűen megfogalmazhatóak, és meggyőződésem, hogy ugyanilyen "egyszerűen" meg is válaszolhatóak.
|
| Előzmény: [452] R.R King, 2009-11-01 17:26:23 |
|
| [452] R.R King | 2009-11-01 17:26:23 |
 Szerintem akkor érdemes matematikával foglalkoznod, ha örömöd leled a feladatok megoldásában, egy-egy bizonyítás megértésében. Mondjuk ez attól is függ, hogy milyen céljaid vannak a matematikában...Én úgy látom, hogy az lehet a gond, hogy rögtön a matematika legnehezebb problémáit akarod megoldani. Ez nem jelenti azt, hogy nem járhatsz sikerrel, de szerintem mint minden másban is a fokozatosság elvét kellene követned. A kezdő hegymászó sem rögtön a Himaláját veszi célba. Esetleg beíratkozhatsz az egyetemre ahogy írtad is régebben..Próbáld meg a belinkelt fórumon is a dolgot.
Üdv. R.R
|
|
|
| [450] bily71 | 2009-11-01 12:19:38 |
 Kösz a tanácsot!
Azt én is észrevettem, hogy egyedül maradtam. Lehetséges, hogy annyi butaságot hordok itt össze, hogy már unják a fórumozók, vagy nem fogalmazok elég érthetően, vagy egyszerűen a téma unalmas.
Rengeteg ötletem van a számelméleti kérdésekkel kapcsolatban, de nem sok segítséget kapok, annak ellenére, hogy az általam használt módszerek egyátalán nem bonyolultak. Pedig szükségem volna a segítségre, mert nem tudom eldönteni, hogy egy-egy gondolatmenetem hibás-e, hisz én csak egy kontár vagyok.
A matematikai ismereteim elég hiányosak, így nem tudom mit lehet, vagy nem lehet, vagy, hogy melyik ötletem használható. Az is problémás nekem, hogy lefordítsam a gondolatomat a matematika nyelvére, nagyon kevés formulát, tételt vágok fejből, a képleteket is innen-onnan böngészem, mert a jelölések nagy részét sem ismerem.
|
| Előzmény: [449] R.R King, 2009-11-01 09:16:17 |
|
| [449] R.R King | 2009-11-01 09:16:17 |
 Üdv. Mivel kevesen válaszolnak arra, amit a Goldbach-sejtésről írsz ezért adnék egy tanácsot: Nézz körül a lenti fórumon. Az egyik fórumozó komoly matematikus, a Rényi Intézet egyik számelmélésze. Ő biztosan segít lellenőrizni amit írtál. Van számelmélet topic, de asszem van külön a Goldbach-sejtésről is. http://forum.index.hu/Topic/showTopicList?t=26
|
| Előzmény: [448] bily71, 2009-11-01 08:59:04 |
|
|
|
| [446] bily71 | 2009-10-31 17:27:46 |
 Egy kis probléma lépett föl. Az np n(mod (2p-2)) kongruencia nem teljesül, akkor, ha p>5, és n<p, azaz n p-nél kisebb páratlan prím, vagy ennek többszöröse. Ez megnehezíti az általánosítást. Továbbá nem sikerült még megtalálnom az általános rekurziót, ami a binomiális együtthatókból állítja elő az Nnm sorozatot. Viszont találtam más összefüggéseket is, ami segítségünkre lehet. n(mod (2p-2)) kongruencia nem teljesül, akkor, ha p>5, és n<p, azaz n p-nél kisebb páratlan prím, vagy ennek többszöröse. Ez megnehezíti az általánosítást. Továbbá nem sikerült még megtalálnom az általános rekurziót, ami a binomiális együtthatókból állítja elő az Nnm sorozatot. Viszont találtam más összefüggéseket is, ami segítségünkre lehet.
Folyt. köv.
|
| Előzmény: [445] bily71, 2009-10-30 19:13:30 |
|
|
|
| [443] bily71 | 2009-10-29 23:19:11 |
 A kis Fermat szerint nm n(mod m), amennyiben m n(mod m), amennyiben m P, azaz prím. A [428]-ban leírt (1), és (3)-ból következik, hogy np P, azaz prím. A [428]-ban leírt (1), és (3)-ból következik, hogy np n(mod (2p-2)). n(mod (2p-2)).
Vizsgáljuk meg a következő felbontást!
np=(np-n)+n=n(np-1-1)+n
Mivel nm-1m=(n-1)(nm-1+nm-2+...+n+1),
ezért np=n(n-1)(np-2+np-3+...+n+1)+n.
Ha p=3, akkor n3=n(n-1)(n+1)+n, n>1 esetén 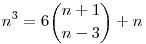 . .
Legyen 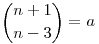 , ekkor n3=6an+n. , ekkor n3=6an+n.
A harisnya tulajdonság miatt 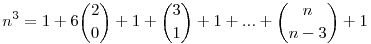 . .
Legyen 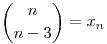 , és írjuk fel a következő felbontást: n3=6an+n=6(an+b)+(n-6b). , és írjuk fel a következő felbontást: n3=6an+n=6(an+b)+(n-6b).
Ekkor an+b nem bontható n-6b darab olyan szám összegére, amely számok az xn sorozat egymásutáni tagjai, mert nem teljesülnek bizonyos oszthatósági feltételek. De ezt már csak holnap látjuk be.
|
| Előzmény: [442] bily71, 2009-10-27 22:15:08 |
|
| [442] bily71 | 2009-10-27 22:15:08 |
 Két okból is lehetetlen, hogy an+b felbotható n-(2m-2)b tagú összegre, ahol a tagok az xn sorozat tagjai.
Egyrészt, mert, míg n 1 1 -1(mod 2), addig n -1(mod 2), addig n 1(mod (2m-2)), és n 1(mod (2m-2)), és n -1(mod (2m-2)) nem ugyanazt a maradékosztályt jeleni, ha m>2. -1(mod (2m-2)) nem ugyanazt a maradékosztályt jeleni, ha m>2.
Másrészt az xn sorozat diferenciája nem konstans.
Ezt először megmutatjuk az m=3 kitevő esetén, aztán megpróbálunk általánosítani, végül megmutatjuk m=4 esetén is, teljessé téve a bizonyítási kisérletet.
Nem akarom elsietni, hisz Wiles-nak 8 éve ment rá, és azt hiszem nem véletlenül.
|
| Előzmény: [440] bily71, 2009-10-27 14:05:31 |
|
| [441] Maga Péter | 2009-10-27 19:56:38 |
 Idézek Henryk Iwaniec és Emmanuel Kowalski Analytic Number Theory című művéből. Az 5. fejezet 5.7 pontjában mondja ki a Grand Riemann Hypothesis-t. Ezután "Remarks. Needless to say we believe that every L-function (subject to our definition in Section 5.1) satisfies the Grand Riemann Hypothesis. Yet, proving this even for one L-function would be an achievement on a historical scale for human beings. (...) On a negative note this superb uniformity could be a reminder how slim prospects are to prove the GRH in our lifetime. No tools of current analytic number theory are capable of treating the questions for which the GRH provides easy answers." Iwaniec a téma (analitikus számelmélet) egyik legelismertebb szakértője a világon.
|
|
|
| [439] bily71 | 2009-10-27 11:51:42 |
 Javítás: m=2 esetén az an sorozat nem a természetes számok sorozata, hanem a természetes számok összege részösszegsorozata, de ez a lényegen nem változtat, a táblázatot kijavítom, mindjárt folytatom.
|
| Előzmény: [438] bily71, 2009-10-27 11:24:20 |
|
| [438] bily71 | 2009-10-27 11:24:20 |
 Azt, hogy (a+b) végtelen sok esetben bontható n-2b darab egymásutáni természetes szám összegére, a következőképp láthatjuk be:
nm=(2m-2)an+n, ahol az an számok egy sorozatot képeznek, m=2 esetén ez a természetes számok sorozzata.
Készítsünk egy táblázatot, mely a természetes számokat összegzi, soronként mindig a kövezkező tagtól kezdve, így felírhatjuk az 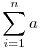 összes részösszegét! összes részösszegét!
| an |
1 |
2 |
3 |
4 |
5 |
... |
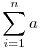 |
1 |
3 |
6 |
10 |
15 |
... |
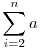 |
|
2 |
5 |
9 |
14 |
... |
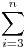 |
|
|
3 |
7 |
12 |
... |
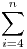 |
|
|
|
4 |
9 |
... |
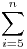 |
|
|
|
|
5 |
... |
|
A táblázatban minden természetes szám megtalálható, ezért alkalmas x,y,z-re igaz, hogy x2+y2=z2.
Az x=3, y=4, z=5 számok alkalmasak, mivel 52 egyik felbontása 52=2.11+3, itt 11-et kell felbontani olyan kéttagú összegre, hogy a tagok felírhatók egymásutáni természetes szám összegént. Mivel az összegben 2.11 mellett 3, azaz 3 db. egyes áll, és a különbségsorozat minden tagja 2k+1 alakú, ezért csak egy megoldás létezhet: 2.11=(2.4)+(2.3+(2.4).
m>2 esetén nem kell a három alkalmas szám nemlétét igazolni, elég azt megmutatni, hogy az
nm=(2m-2)an+n=(2m-2)(an+b)+(n-(2m-2)b)
esetén az an+b tag nem írható fel n-(2m-2)b darab olyan szám összegeként, amelyek az an sorozat egymásutáni tagjai.
Tehát ezt kell bizonyítani.
Folyt. köv.
|
| Előzmény: [437] bily71, 2009-10-27 07:08:10 |
|
| [437] bily71 | 2009-10-27 07:08:10 |
 Ha n>1, akkor
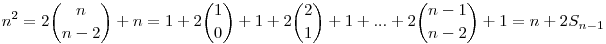 , ,
ahol Sn-1 az első n-1 természetes szám összege.
Legyen 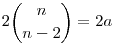 , ekkor , ekkor
n2=2a+n=2(a+1)+(n-2)=2(a+2)+(n-4)=...
általánosan: n2=2(a+b)+(n-2b),
ha (a+b) felírható n-2b darab egymásutáni természetes szám összegeként, akkor n2-et sikerült felírni a különbségsorozat részösszegeként.
Folyt. köv.
|
| Előzmény: [436] bily71, 2009-10-26 18:13:12 |
|
| [436] bily71 | 2009-10-26 18:13:12 |
 Akkor folytassuk!
Körvonalazni is nehéz azt a tényezőt, ami megkülönbözteti az m=2 esetet a többitől, annyira el van rejtve, de végre sikerült megfogalmazni, hogy mit is akarok bizonyítani.
Írjuk fel újból az Nn2 sorozat tagjait, különböző felbontásokban!
12=1,
22=2.1+2,
32=2.3+3=2.4+1,
42=2.6+4=2.7+2=2.8+0,
52=2.10+5=2.11+3=2.12+1,
s.í.t.
Figyeljük meg a következő felbontás minden részletét!
52=32+42,
azaz
2.11+3=(2.4+1)+(2.7+2),
ahol a jobb oldal második tagja tovább bontható:
2.7+2=(2.3+1)+(2.4+1).
Bocs, mindjárt folytatom.
|
| Előzmény: [435] bily71, 2009-10-23 21:45:04 |
|
| [435] bily71 | 2009-10-23 21:45:04 |
 Ebből a semmitmondónak tűnő összefüggésből még semmitmondóbbnak tűnő dolgok jönnek ki, melyek a paritás mögött bújnak meg.
A levezetés több szálon is fut a fejemben, és ahogy haladok lépésről-lépésre, mindig azt az utat részesítem előnyben, amiről feltételezem, hogy hamarább a célba juttat, és, mivel ez menet közben derül ki, ezért előfordulhat, hogy feleslegesen szabott feltételeket, vagy felesleges lépéseket tartalmaz.
Ma már nem folytatom, holnap a befejezés következik.
|
| Előzmény: [434] bily71, 2009-10-23 18:58:53 |
|
| [434] bily71 | 2009-10-23 18:58:53 |
 Az Nnm sorozatot mindig 1-gyel kezdjük, a táblázatokban csak azért kezdtük 0-val, hogy azonosítani tudjuk azt a számot, amivel ha elosztjuk az első különbségsorozat bármely tagját, 1-et kapunk maradékul.
Nézzük hogy alakul Nn2:
12=1,
22=1+(2+1),
32=1+(2+1)+(4+1)...
általában:
n2=1+(2.1+1)+...+(2(n-1)+1).
A képzési szabály szerint, n, és a zárójeles tagok számának paritása ellentétes.
Mivel a zárójeles tagok páratlanok, a kis Fremat n2 nmod 2 csak akkor teljesül, ha az összeghez hozzáadunk 1-et. nmod 2 csak akkor teljesül, ha az összeghez hozzáadunk 1-et.
Mivel  1Nn2 diferenciája 2, előfordulhat, hogy bizonyos részsorozatainak összegére teljesülnek a feltételek, azaz négyzetszámot kapunk eredményül. 1Nn2 diferenciája 2, előfordulhat, hogy bizonyos részsorozatainak összegére teljesülnek a feltételek, azaz négyzetszámot kapunk eredményül.
Térjünk vissza a példához:
32=(2.4+1)=(2.4)+1,
42=(2.3+1)+(2.4+1)=(2.3)+(2.4)+1+1=(2.7)+2.
Itt n, és a zárójeles tagok számának paritása megegyezik.
Mivel páros darab 1-es összege páros, páratlané pedig páratlan, ezért, ez csak úgy lehetséges, ha n, és a 2-vel szorzott számok összegének paritása ellentétes.
Na ez az a jelentéktelennek tűnő mozzanat, ami az m>2 kitevőjű sorozatokban nem lehetséges.
|
| Előzmény: [433] bily71, 2009-10-23 09:05:09 |
|
| [433] bily71 | 2009-10-23 09:05:09 |
 De az, hogy  1Nn2 elsőrendű számtani sorozat, önmagában még kevés, ehhez jön még, hogy d1=m azaz a diferenciája egyenlő a kitevővel, így, m=2 esetben (3) tulajdonképp a kis Fermat-tétel, n2 1Nn2 elsőrendű számtani sorozat, önmagában még kevés, ehhez jön még, hogy d1=m azaz a diferenciája egyenlő a kitevővel, így, m=2 esetben (3) tulajdonképp a kis Fermat-tétel, n2 nmod 2. nmod 2.
Folyt. köv.
|
| Előzmény: [432] bily71, 2009-10-22 22:06:25 |
|
| [432] bily71 | 2009-10-22 22:06:25 |
 Minden tag 2x+1 alakú, ahol x>1, tehát a sor eleji 1-est nem soroljuk a tagok közé.
Ha összeadjuk az első y tagot, és hozzáadjuk a sor eleji 1-est, ezt kapjuk:
1+(2+1)+(4+1)+...+(2y+1)=(y+1)2.
Az előző példa azt mutatja, hogy a következő egyenletnek
1+(2+1)+...+(2y+1)=(2x1+1)+(2x2+1)+...+(2xz+1)
van megoldása, annak ellenére, hogy a bal oldalon a tagok összegéhez hozzá kellett adni egyet, hogy négyzetszámhoz jussunk, a jobb oldalon pedig a tagok összege négyzetszám.
Ez azért lehetséges, mert az Nn2 másodrendű számtani sorozat, aminek a különbségsorozata elsőrendű számtani sorozat, az m>2 kitevőjű sorozatok különbségsorozata viszont nem, mivel, ha kitevő m, akkor a különbségsorozat m-1-edrendű. Ha m=1, akkor pedig nullarendű.
|
| Előzmény: [431] bily71, 2009-10-22 20:16:47 |
|



 N).
N).  m,i az Nnm sorozat különbségsorozatainak első tagjait, ekkor a megadható a következő általános(!) rekurzió, mely a binomiális együtthatókból állítja elő az Nnm sorozatot:
m,i az Nnm sorozat különbségsorozatainak első tagjait, ekkor a megadható a következő általános(!) rekurzió, mely a binomiális együtthatókból állítja elő az Nnm sorozatot:  cm-(c-1)m.
cm-(c-1)m. 

 n(mod (2p-2)) kongruencia nem teljesül, akkor, ha p>5, és n<p, azaz n p-nél kisebb páratlan prím, vagy ennek többszöröse. Ez megnehezíti az általánosítást. Továbbá nem sikerült még megtalálnom az általános rekurziót, ami a binomiális együtthatókból állítja elő az Nnm sorozatot. Viszont találtam más összefüggéseket is, ami segítségünkre lehet.
n(mod (2p-2)) kongruencia nem teljesül, akkor, ha p>5, és n<p, azaz n p-nél kisebb páratlan prím, vagy ennek többszöröse. Ez megnehezíti az általánosítást. Továbbá nem sikerült még megtalálnom az általános rekurziót, ami a binomiális együtthatókból állítja elő az Nnm sorozatot. Viszont találtam más összefüggéseket is, ami segítségünkre lehet. 
 1Nn2 diferenciája 2, előfordulhat, hogy bizonyos részsorozatainak összegére teljesülnek a feltételek, azaz négyzetszámot kapunk eredményül.
1Nn2 diferenciája 2, előfordulhat, hogy bizonyos részsorozatainak összegére teljesülnek a feltételek, azaz négyzetszámot kapunk eredményül.