| [52] Maga Péter | 2009-03-19 22:49:39 |
 Félreértés ne essék, nem vagyok én az elemi matek fáklyás szószólója. Csupán Róbert Gida határozott kijelentésére reagáltam.
Mondok egy példát. Szerintetek középiskolai módszerekkel be lehet bizonyítani, hogy vannak transzcendens valós számok? És vajon erről mit mondott volna Gauss vagy Liouville (ő bizonyította be először, de az nem egy nyilvánvaló meló, pláne nem középiskolás rutinnal)? Cantor a halmazelmélettel egy olyan matematikai közlési formát hozott létre, melynek egyik alapvető fogalmával (számosság), a tétel nevetségesen egyszerűvé vált. Azóta a halmazelmélet bevezető fogalmai (köztük a számosság) a középiskolai (legalábbis specmatos, mást nem ismerek) anyag részévé váltak.
Egyszer nekem azt mondta valaki, hogy nagyon valószínűnek tartja, hogy a P-NP-problémát ugyanígy fogják megoldani, kitalálnak egy új nyelvet, amiben el lehet mondani egy korábban elképzelhetetlen bizonyítást. A Riemann-sejtésről nem gondolta ezt, de ott sem tartotta kizártnak.
Szóval csak nyugalom, mélyeket kell lélegezni, meg minden ilyemi... és akkor hátha nem csinál az ember kategorikus kijelentéseket a megérzéseiből.
|
|
| [51] Maga Péter | 2009-03-19 22:26:36 |
 És mégis... Például Erdősék csináltak komplex függvénytan nélküli bizonyítást a prímszámtételre, illetőleg a Dirichlet-tételre (utóbbit Selberggel 1950 körül, előbbit nem tudom). Nem azért, mert bárki megkövetelte, de nekik kijött...
|
| Előzmény: [49] Káli gúla, 2009-03-18 22:33:35 |
|
| [50] Maga Péter | 2009-03-19 22:20:10 |
 Az undergraduate mindenkire érvényes, akinek nincs fokozata (legalábbis szerintem az under + graduate szóelemzés ezt mutatja). Más kérdés, hogy valóban egyetemi hallgatókra szokás használni, de a konkrét esetben Napnál világosabb, hogy a fordulat azt jelenti, hogy az üzemeltetők szerint elképzelhető, hogy nem kell hozzá előismeret. Tehát jelen esetben az undergraduate a (sok más esetben hibás) tükörfordítással értendő.
Tényleg fogalmunk nincs róla, hogy hogyan lehet bizonyítani. Maga a probléma elemi, ezért semmi nem zárja ki, hogy elemi bizonyítás létezzen rá. Csak hogy a cáfolatot ne is említsem: ha ugyanis a Goldbach-sejtés nem igaz, akkor annak van egy tökelemi, esetleg hosszadalmas bizonyítása:).
|
| Előzmény: [48] jonas, 2009-03-18 21:37:00 |
|
| [49] Káli gúla | 2009-03-18 22:33:35 |
 Egy additív számelmélettel foglalkozó könyv előszavában Turán Pál a "Goldbach-problémát" az emberi szellem egyik legnagyobb erőpróbájának nevezte, és azt írta, hogy a legmélyebb tények kutatásánál a tiszta módszereket megkövetelni "kb. olyan volna, mintha a Himalája megmászóitól azt követelnénk, hogy csak kezüket használják, ami lehet követelmény egy tornatermi kötél megmászásánál".
|
| Előzmény: [47] Maga Péter, 2009-03-18 19:06:24 |
|
|
| [47] Maga Péter | 2009-03-18 19:06:24 |
 Vagy ki tudja...
Egyrészt a http://garden.irmacs.sfu.ca/ például ajánlja undergraduate embereknek is.
Másrészt még megoldott problémák esetében is elég merész olyan dolgokat kijelenteni, hogy valahogyan nem kezelhetők.
|
| Előzmény: [42] Róbert Gida, 2007-12-21 14:41:30 |
|
|
| [45] MTM | 2009-03-17 19:59:55 |
 Tudja valaki, hogy adtak-e már arra választ, hogy minden 6-nál nagyobb páros szám előáll-e
-3 prím összegeként?
-4 prím összegeként?
|
|
|
| [43] Doom | 2007-12-21 15:48:36 |
 Én viszont örülük, hogy megosztotta velünk, ő legalább gondolkodott rajta (vagy manapság lehet, hogy a "gondolkodott" már önmagában nagy erény). És egyszer még kiderülhet, hogy legyőzthető középiskolás módszerrel... :) Fő az optimizmus! :D
|
|
|
|
| [40] Róbert Gida | 2007-12-21 13:37:13 |
 "A 2 mint prím, csak a (2;2) pontnak lehet koordinátája" Ez megint zöld. Azt egyébként tudod mi a (páros) Goldbach sejtés? Minden 2-nél nagyobb páros szám előáll két prím összegeként.
Ezt láttad be? Szerintem nem. Az egyeneseken akkor, ha jól értem számolgatsz (büvészkedsz), csak azt nem látom, hogy minden egyenesen lenne (p,q) koordinátájú pont, ahol p,q prímek. Valóban ez ekvivalens lenne a Goldbach sejtéssel, hiszen akkor a pont ***értéke*** p+q=2n volna.
|
| Előzmény: [38] voo7doo7, 2007-12-21 13:11:22 |
|
| [39] voo7doo7 | 2007-12-21 13:20:06 |
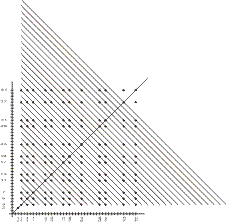
 Bizonyításom lényege az, hogy 2p-ig a koordináta rendszerben szereplő különböző páros számok (darab)száma megegyezik a különböző páros számok valódi (darab)számával 2p-ig, a koordináta rendszerben csak azok páros számok szerepelnek, amik felírhatók két prím összegeként, tehát a Goldbach-sejtés igaz.
|
| Előzmény: [34] Róbert Gida, 2007-12-21 00:43:24 |
|
| [38] voo7doo7 | 2007-12-21 13:11:22 |
 A 2 mint prím, csak a (2;2) pontnak lehet koordinátája, mivel ha más prímmel állna, nem kapnánk a pont értékének páros számot. Az azonos értékű pontokra állítsunk egy egyenest. Ezek az egyenesek lesznek párhuzamosak. A képlet az egyenesk számára azért (2p-6)/2+1 , mert a háromszög alapjának hossza 2p-6, de az egyenesek a háromszög alapját mindig páratlan koordinátánál fogják metszeni, ezért osztjuk 2-vel. Ha van egy x egység hosszú szakaszunk, és egységenkéntakarjuk felosztani úgy hogy legyen kezdő- és végpontja is, akkor x+1 pontra van szükségünk. Ez esetünkben azt jelenti, hogy az egyenesek száma (2p-6)/2+1.
|
 |
|
| [37] Cckek | 2007-12-21 08:56:21 |
 Talán a párhuzamos egyenesek heleyet jobb lenne két azonos értékű pontot ekvivalensnek tekinteni.
A(p1,p2) B(p3,p4)<=>p1+p2=p3+p4. B(p3,p4)<=>p1+p2=p3+p4.
Ebben az esetben q egyenlő lenne az ekvivalenciaosztályok számával.
|
| Előzmény: [36] Cckek, 2007-12-21 08:45:51 |
|
| [36] Cckek | 2007-12-21 08:45:51 |
 Nagy p primre elég nehéz lehet megállapítani a A(p1,p2) kordinátájú pontok számát, ahol p1<p,p2<p primek. Ezért nem értem ezket a q-ra és e-re levezetett képleteket, de lehet csak én vagyok buta.
|
| Előzmény: [35] AzO, 2007-12-21 00:46:02 |
|
| [35] AzO | 2007-12-21 00:46:02 |
 Nagy nehezen en is eljutottam a kepletig, amit egyaltalan nem ertek, de utana (ha felteszem, hogy azt te valamilyen uton-modon belattad, es ezt en meg el is hiszem, akkor) az e es a q kozti kulonbseget sem ertem igazan, igy hat arra kernelek, hogy az egeszet ird le elolrol, de mindent nagyon precizen definialva. Peldaul (ha vagy olyan kedves, es ezt megteszed nekem) ne irj olyat, hogy e az egyenesek szama. Milyen egyenesek szama? Kozvetlen utana ne irj olyat, hogy "tehat a paros szamok szama", hisz honnan tudod, hogy minden paros szamhoz tartozik ilyen tipusu egyenes (pont ezt akarjuk bizonyitani, mert ezzel a v injektiv lekepezesed szurjektiv is lenne, ez ugye azt jelenti, hogy minden egyeneshez nyilvan csak egy paros szam tartozik, de honnan tudod, hogy minden paros szamhoz tartozik ilyen egyenes). Ne irj olyat, hogy jeloljuk a primeket, hanem ird meg, hogy a tengelyen gondoltad a jelolest. Es ne felejts el dolgokat, mint peldaul, hogy te a felvett pontok kozul csak azokon at huzol egyeneseket, amiknek az "erteke" paros.. Stb.... Ha mindez megtortenik, akkor hamarabb feny derul az igazsagra, mert igy erdemben nem tudunk foglalkozni a problemaval. Elore is koszi!
|
|
| [34] Róbert Gida | 2007-12-21 00:43:24 |
 Végigolvasva a ***bizonyítást*** számomra úgy tűnik, hogy 2p-t *sikerült?* neki felbontania 2 prím összegére minden p prímre, ami persze triviális 2p=p+p. Ami az eredeti Goldbach sejtéstől elég távol van.
Hatodik érzékem azt súgja, hogy ez egy rossz bizonyítás.
|
| Előzmény: [33] leni536, 2007-12-21 00:14:14 |
|
|
| [32] Róbert Gida | 2007-12-20 23:01:01 |
 windows beépített programjával paint-tel lehet másként elmenteni a képet jpg-ként. Majd menj kepfeltoltes-ra ott fel lehet tölteni a képet jpg-ként, regisztráció nélkül. Gondolatébresztőként feltettem egy térképet, amin pont egy Goldbach nevű település található Goldbach
|
| Előzmény: [29] voo7doo7, 2007-12-20 20:38:33 |
|
| [31] voo7doo7 | 2007-12-20 21:03:28 |
 Ne velem foglalkozzatok, hanem azzal amit leírtam és azt mondjátok meg hogy hol következtettem rosszul. Azt mondd meg hol a hiba, engem nem az érdekel hogy mennyire tudsz kötözködni, hanem azt írd le mi a rossz, mi a hiba. Különben meg sok sikert.
|
| Előzmény: [30] PAL, 2007-12-20 20:56:55 |
|
|
| [29] voo7doo7 | 2007-12-20 20:38:33 |
 mondjuk egy 5 megás képből csinálj 50kb-ost úgy hogy azon láss is valamit...
|
|
|










 B(p3,p4)<=>p1+p2=p3+p4.
B(p3,p4)<=>p1+p2=p3+p4.

