|
| [557] Maga Péter | 2010-03-07 23:18:24 |
 Először is üdvözlom a Kollégát!:P
Másodsorban nem látom, hogy miben új ez a k 3nm 3nm n n m a korábbi k m a korábbi k 6nm 6nm n n m-hez képest. m-hez képest.
Ugyanis minden páratlan szám felírható 3nm n n m alakban, m=1-et, és mindkétszer a mínuszt választva 2n-1 adódik, ami valóban befutja a páratlan számokat. m alakban, m=1-et, és mindkétszer a mínuszt választva 2n-1 adódik, ami valóban befutja a páratlan számokat.
A párosokra pedig a következő van. Ekvivalensek:
(i) 2k felírható 3nm n n m alakban; m alakban;
(ii) k felírható 6NM N N M alakban. M alakban.
(ii)  (i): Legyen k=6NM (i): Legyen k=6NM N N M. Ekkor 2k=12NM M. Ekkor 2k=12NM 2N 2N 2M, vagyis n=2N, m=2M jelöléssel 2k=3nm 2M, vagyis n=2N, m=2M jelöléssel 2k=3nm n n m. m.
(i)  (ii): Legyen 2k=3nm (ii): Legyen 2k=3nm n n m. Ekkor n,m párosak, különben 3nm m. Ekkor n,m párosak, különben 3nm n n m páratlan lenne. Legyen n=2N, m=2M. Ekkor 2k=12NM m páratlan lenne. Legyen n=2N, m=2M. Ekkor 2k=12NM 2N 2N 2M, azaz k=6NM 2M, azaz k=6NM N N M. M.
Ha nem néztem el semmit (ami persze bőven lehetséges), akkor így nem kapunk semmi újat...
|
| Előzmény: [554] beduin, 2010-03-07 17:38:06 |
|
|
|
| [554] beduin | 2010-03-07 17:38:06 |
 Üdvözlök mindenkit, engdjétek meg, hogy bemutatkozzam: a nevem Szerencsés Beduin.
Matematikus vagyok, és időmet nem sajnálva megvizsgáltam bily71 függvényét. Nem sokra jutottam, de eljárását követve a számolást kiterjesztettem a k 3nm 3nm n n m és a k m és a k 4nm 4nm n n m számokra, mivel minden prím véges sok kivétellel 3k m számokra, mivel minden prím véges sok kivétellel 3k 1, 4k 1, 4k 1, vagy 6k 1, vagy 6k 1 alakú. Utóbbit bily71 már megszámolta. 1 alakú. Utóbbit bily71 már megszámolta.
Ezek közül a k 3nm 3nm m m m eset érdekesnek bizonyult, és egy trükkel az egészrészek elhagyása nélkül megállapítható, hogy f3(x) korlátos-e vagy sem. m eset érdekesnek bizonyult, és egy trükkel az egészrészek elhagyása nélkül megállapítható, hogy f3(x) korlátos-e vagy sem.
|
| Előzmény: [552] Fálesz Mihály, 2010-03-06 19:14:59 |
|
| [553] bily71 | 2010-03-06 22:07:57 |
 Ezt mind értem, és nem is akartam elhagyni az egészrész jeleket, hiszen már egyszer próbálkoztam ilyennel és nem sikerült. Nem erre gondoltam, hanem arra, hogy hátha összevethető egy hasonló formulával, amiről tudjuk egy másik összefüggésből, hogy nem korlátos. Ha lenne ilyen, az lenne a beduin szerencséje.
|
| Előzmény: [552] Fálesz Mihály, 2010-03-06 19:14:59 |
|
| [552] Fálesz Mihály | 2010-03-06 19:14:59 |
 Nem.
Maga Peti valamikor korábban világosan megírta, mi a baj az ilyen próbálkozásokkal. A szitában sokkal, de sokkal több tag van, mint maga az eredmény, és nincs esély pl. az egészrész jelek elhagyásából fakadó hiba megbecslésére. Mit is kezdjünk azzal, ha egymilliárdig szitálgatjuk a prímeket, közben pedig elhagyunk 1010000 egészrészt?
|
| Előzmény: [551] bily71, 2010-03-06 10:20:43 |
|
|
| [550] bily71 | 2010-03-06 10:15:07 |
 Nem, én követlek meg, és Robert Gidát, amiért összevontam olyan tagokat is, ami pontatlan eredményhez vezet. Mert, míg ![\left[\frac{a}{b}\right]\pm\left[\frac{c}{b}\right]=\left[\frac{a\pm{c}}{b}\right]](keplet.cgi?k=D17DC030DC9B7CA2) minden esetben igaz, addig minden esetben igaz, addig ![c\left[\frac{\left[\frac{a}{b}\right]}{d}\right]=\left[\frac{ac}{bd}\right]](keplet.cgi?k=9296B57B56D45DBA) nem minden esetben teljesül, sőt elég nagy eltérések is lehetnek. nem minden esetben teljesül, sőt elég nagy eltérések is lehetnek.
Biztos unjátok már a fejemet, de azért leírom helyesen: ha 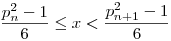 , akkor , akkor
![f(x)=2\sum_{d|P(p_n)}\mu(d)\left[\frac{\left[\frac{p_n^2-(g(d))^2}{6}\right]}{d}\right]-n-\frac{p_n^2-1}{6},](keplet.cgi?k=046583E48A7C92B0)
ahol pn az n-edik 3-nál nagyobb prím, 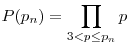 , ,  (d) a Moebius-függvény, g(d) jelöli d legnagyobb prímosztoját, g(1)=1. Szedjük szét, és legyen (d) a Moebius-függvény, g(d) jelöli d legnagyobb prímosztoját, g(1)=1. Szedjük szét, és legyen ![A(x)=2\sum_{d|P(p_n)}\mu(d)\left[\frac{\left[\frac{p_n^2-(g(d))^2}{6}\right]}{d}\right]-n](keplet.cgi?k=8E0066D743066C6B) , és , és 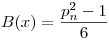 . .
Az 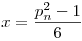 helyeken B(x)=x, vagyis, ha csak ezeken a helyeken ábrázoljuk, akkor a pontok az y=x egyenesen helyezkednek el. A függvény ezeken a helyeken helyettesíthető b(x)=x-szel, és b'(x)=1. helyeken B(x)=x, vagyis, ha csak ezeken a helyeken ábrázoljuk, akkor a pontok az y=x egyenesen helyezkednek el. A függvény ezeken a helyeken helyettesíthető b(x)=x-szel, és b'(x)=1.
A(x)-et kellene megvizsgálni, megfelelően helyettesíteni, és meghatározni a helyettesítő függvény deriváltját, aztán venni a deriváltak különbségét, amely megmutatná f(x) menetét.
f(x)-et úgy kaptam, hogy képeztem egy szorzótáblát, összeszoroztam a 6k 1 alakú számokat, a táblázatban k értékét tüntettem fel. Mivel (6n 1 alakú számokat, a táblázatban k értékét tüntettem fel. Mivel (6n 1)(6m 1)(6m 1)=6(6nm 1)=6(6nm n n m) m) 1=6k 1=6k 1, ebből k=6nm 1, ebből k=6nm n n m=n(6m m=n(6m 1) 1) m, ezért a táblázat minden sora megfelel egy olyan számsorozatnak, ahol 6m m, ezért a táblázat minden sora megfelel egy olyan számsorozatnak, ahol 6m 1 minden többszörösére két szám jut, tulajdonképp két számtani sorozatot fésültünk egymásba. 1 minden többszörösére két szám jut, tulajdonképp két számtani sorozatot fésültünk egymásba.
Azon számokat keressük, amelyek nem szerepelnek a tálázatban, azaz egyik ilyen sorozatnak sem tagjai. Szimmetria okokból elég, ha csak a főátló jobb oldalán számoljuk meg, hány darab számot találunk x-ig soronként. Azokat a sorokat, ahol 6k 1 összetett kihagyhatjuk a számolásból. Tulajdonképp a főátlótól jobbra, és egy görbétől balra lévő különböző értékű számok számát kell meghatároznunk. 1 összetett kihagyhatjuk a számolásból. Tulajdonképp a főátlótól jobbra, és egy görbétől balra lévő különböző értékű számok számát kell meghatároznunk.
A számolás menete: valamely prím sorában elmegyünk a főátlóig, ezt a számot x-szel jelöljük, addig biztos, hogy minden szám már szerepelt valahol, aztán e sor felett minden prím sorában megkeressük a főátlóban lévő számmal egyenlő, vagy a nála kisebbek közül a legnagyobbat, ebből kivonjuk a főátló és e sor metszésében lévő számot, ezután elosztjuk a sor prímjével, az eredményt kirosatáljuk, aztán megszorozzuk kettővel, ugyanis minden többszörösre két szám jut, a sorok eredményeit összegezzük, ebből még kivonjuk a vizsgált sorok számát, és vesszük x és az összeg különbségét és az eredmény f(x).
|
| Előzmény: [547] Maga Péter, 2010-03-05 20:17:37 |
|
| [549] Fálesz Mihály | 2010-03-06 09:28:09 |
 A Legendre-formulából és az 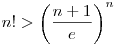 becslésből következik, hogy becslésből következik, hogy
![\log (n!) =
\sum_{p\le n} \left( \sum_{k=1}^\infty
\bigg[\frac{n}{p^k}\bigg]\right)\log p <
\sum_{p\le n} \left( \sum_{k=1}^\infty
\frac{n}{p^k}\right)\log p =
n \sum_{p\le n} \frac{\log p}{p-1},](keplet.cgi?k=06D7BE2DA9B1A1AD)
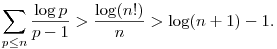
(A felső becslés is igaz (a -1 helyett egy másik, pozitív konstanssal), ehhez meg kell becsülni a az egészrészjelek elhagyásából származó hibát.)
A jobboldal végtelenhez tart, tehát végtelen sok prím van. ;-)
|
| Előzmény: [548] bily71, 2010-03-05 21:49:02 |
|
| [548] bily71 | 2010-03-05 21:49:02 |
 Azt én is gondoltam, hogy ez nem olyan egyszerű, hiszen vannak olyan függvények, amelyek képlettel nem is adhatók meg.
De például azt, hogy végtelen sok prím van, nem tudjuk levezetni a Legendre-formulából, (legalábbis én nem tudom), mégis biztosan tudjuk, ![\pi(x)= \sum_{d|P(\sqrt{x})}\mu(d)\left[\frac{x}{d}\right]+\pi(\sqrt{x})-1](keplet.cgi?k=5E3969023525E664) nem korlátos, ebből következik, hogy nem korlátos, ebből következik, hogy ![g(x)=\sum_{d|P(\sqrt{x})}\mu(d)\left[\frac{x}{d}\right]](keplet.cgi?k=29F2FED7A9DA9878) sem az. sem az.
f(x)-et hasonló módszerrel definiáltam, lehet, hogy elképesztően naív vagyok, de úgy gondoltam, hogy a hasonlóság miatt f(x) addig alakítgatható, míg összehasonlítható nem lesz a Legendre-formulából ismert összegzéssel, mert, mi mást csinálnak a matematikusok, mikor függvényeket vizsgálnak, ha nem összehasonlítgatnak.
|
| Előzmény: [547] Maga Péter, 2010-03-05 20:17:37 |
|
| [547] Maga Péter | 2010-03-05 20:17:37 |
 Ezt a sorozatot megint nem értem. De valahogy úgy érzem, hogy
"Tehát, feltéve, hogy a fenti gondolatmenetben nincs logikai bukfenc, az ikerprím-sejtés visszavezethető az f(x) függvény vizsgálatára, vagyi az ikerprím-sejtés nevű fenevadat becserkésztük, most már csak le kell teríteni."
elképesztően naiv. Persze minden attól függ, hogy mit értesz becserkészés alatt. De ezen az elven legyen
A) x>2-re legyen M(x) az x-nél kisebb Mersenne-prímek száma. Most azt kell meggondolni, hogy M(x) korlátos-e. Ha nem, akkor végtelen sok páros tökéletes szám van.
B) x>2-re legyen
R(x)=min {x, min {t:  s s C: C:  (s)=0, Re(s)>1/2+1/x, |Im(s)|=t}}. (s)=0, Re(s)>1/2+1/x, |Im(s)|=t}}.
(Itt helyesen inf kellene a második min helyett, de valamiért nem hajlandó így lefordítani, értsétek jól, üres halmazra ez + .) Most azt kell meggondolni, hogy R(x) korlátos-e. Ha nem, akkor igaz a Riemann-sejtés. .) Most azt kell meggondolni, hogy R(x) korlátos-e. Ha nem, akkor igaz a Riemann-sejtés.
Tehát az, hogy egy problémát át tudunk konvertálni egy olyanná, hogy egy függvény korlátossága legyen eldöntendő, nem jelenti azt, hogy a probléma elérhető közelségbe került. Nincs olyan gép, amibe ha bedobsz egy függvényt, akkor megmondja, hogy korlátos-e vagy nem. Ha jól kiszitálod az általad definiált f-et, és eldöntöd vele az ikerprím-sejtést, én megkövetlek, és minden fórumon, amihez közöm van, elismerem, hogy tévedtem.
|
| Előzmény: [539] bily71, 2010-03-05 12:32:10 |
|
|
|
|
| [543] bily71 | 2010-03-05 16:32:52 |
 Ez igaz, de a megfelelő erősségű detektor nem biztos, hogy az eddigiek továbbfejlesztett változata, lehet, hogy egészen más a működési elve.
Senki nem lehet mestere egy szakmának tanulás nélkül, épp ezért küldtem el a felvételi lapot az ELTE-t megjelölve első helyen. De a tanuás nem minden, motiváció is kell a sikerhez.
|
| Előzmény: [540] Csimby, 2010-03-05 12:55:28 |
|
|
| [540] Csimby | 2010-03-05 12:55:28 |
 A beduinnak szerencséje volt. A matematikában a szerencse kevés. Ott van előtte a munka, "amikor kifejleszted a fémdetektort"! (persze az jó ha szerencséd van és jó helyen keresgélsz vele, de csak a szerencse nem elég) De hogy a példádnál maradjak - és ezt mondja neked itt mindenki a fórumon - a Goldbach-sejtés egy olyan probléma amiért már a sivatag minden négyzetcentiméterét átvizsgálták 10m-es mélységben, tehát ha a felszínen lenne a megoldás, megtalálták volna. Mélyebben kell keresni, amihez még erősebb detektorok kellenek...
|
| Előzmény: [538] bily71, 2010-03-05 09:53:29 |
|
| [539] bily71 | 2010-03-05 12:32:10 |
 Tehát mégegyszer, hátha nem volt érthető.
Van végtelen sok számsorozatunk, minden 3-nál nagyobb prímhez egy. Írjuk fel képzeletben egyenként a számsorozatokat. Egy biztos, akárhányat is írunk fel, mindig lesznek olyan számok, amelyek egyik sorozatnak sem tagjai.
Tekintsük azon számok sorozatát amelyek az eddig felírt n darab sorozat egyikének sem tagjai, jelöljük ezt An-nel, továbbá képezzünk egy másik számsorozatot, amelynek n-edik tagja az n-edik számsorozat legkisebb olyan száma, amelyik az előző sorozatok egyikének sem tagja, ezt pedig jelölje Bn, és végül jelöljük Cn-nel azon számok sorozatát, amelyek az összes, tehát végtelen sok számsorozatból kimaradtak.
Tegyük fel, hogy Cn véges, ez csak úgy lehetséges, ha An és Bn tagjai egy bizonyos tagtól, mondjuk am-től megegyeznek. Tehát am=bm szükséges feltétel. Persze nem elégséges, mert attól még am+1=bm+1 nem biztos, hogy teljesül, de ez most nem fontos, mert ha azt akarjuk bizonyítani, hogy Cn nem korlátos, elég azt belátni, hogy an bn, vagyis An és Bn megfelelő sorszámú tagjai között az egyenlőség soha nem teljesül. bn, vagyis An és Bn megfelelő sorszámú tagjai között az egyenlőség soha nem teljesül.
Ha am<bn, és m>n, vagyis, ha az An sorozat azon tagjai közül, amelyek a Bn sorozat n-edik tagjánál kisebbek, a legnagyobb sorszáma nagyobb mint n, és ez minden n-re teljesül, akkor az Cn számsorozat nem állhat véges sok tagból.
Azt tudjuk, hogy bn nagyob,vagy egyenlő az n-edik sorozat egy bizonyos tagjával. Jelöljük ezt a tagot xn-nel, tehát x bn. Azt is tudjuk, hogy bn. Azt is tudjuk, hogy 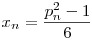 . .
Tekintsük az An sorozat xn-nél kisebb tagjai közül a legnagyobb sorszámát, és rendeljük hozzá xn-hez, ez a sorszám csak m lehet, ugyanis am<bn xn, tehát f(xn)=m. xn, tehát f(xn)=m.
Ha f(xn) szigorún monoton nő, akkor Cn nem lehet véges, ugyanis a3=3<b1=4, vagyis 3>1, ezért, mivel, ha n nő, akkor m=f(xn) is nő, így minden n-re teljesül, hogy am<bn és m>n.
Az f(xn) értéke könnyen kiszámolható a logikai szita segítségével, oly könnyen, hogy Péter szerint nyugodtan betehetjük a gyakorló feladatok közé.
Tehát, feltéve, hogy a fenti gondolatmenetben nincs logikai bukfenc, az ikerprím-sejtés visszavezethető az f(x) függvény vizsgálatára, vagyi az ikerprím-sejtés nevű fenevadat becserkésztük, most már csak le kell teríteni.
|
| Előzmény: [538] bily71, 2010-03-05 09:53:29 |
|
| [538] bily71 | 2010-03-05 09:53:29 |
 Dobjunk el egy aranyérmét a Szaharában, mivel a homok és az arany színe nem sokban különbözik, elég nehéz feladat a megtalálása. Persze kiművelt tudósok hada megfelelő eszközökkel felszerelkezve, mondjuk fémdeterktorokkal, a sivatag minden négyzetcentiméterét átvizsgálva előbb-utóbb megtalálja. Tételezzük fel, hogy arra jár véletlenül egy buta beduin, aki még meg is mosolyogja ezeket a furcsa szerzeteket, akik valami különös szerszámokkal, látszólag céltalanul bolyongnak a sivatagban. Egyszer csak megcsillan valami a napfényben. A beduin felveszi, és örömében zsebrevágja a talált aranyérmét... Tanúság: a beduin egészen más szemszögből vizsgálta a helyzetet, a napfényét az érme csak az ő szemébe tükrözhette, mivel a fény csak egyenes úton terjed, így a csillogást senki más nem láthatta.
|
| Előzmény: [536] Maga Péter, 2010-03-04 21:54:03 |
|
| [537] rizsesz | 2010-03-05 00:01:06 |
 erről hol lehet olvasni :)?
éppen ezt tervezem (bár én több szempontból outlier vagyok, egy idő után a sémák tanulása befejeződött, mert nem erőszakolta rám senki - csak jellemzésként: két matek oktv döntőre elég volt :), ugyanakkor talán pont ezért még fogékonyabb vagyok másra) :)
|
| Előzmény: [532] agysejt, 2010-03-04 14:58:50 |
|
| [536] Maga Péter | 2010-03-04 21:54:03 |
 Bizonyára nem vagyok maximálisan kiművelve matematikatörténeti anekdotákból: nem tudom, mi Lovász esernyője. Gauss összegzése kétségkívül fantasztikus teljesítmény egy 9 éves gyerektől (bár én úgy tudom, csak 6 volt), mindazonáltal nem volt áttörés, nem oldott meg rejtélyeket. Erdős pedig egy korábban ismert tételre adott egy egyszerűbb bizonyítást (személy szerint én az eredeti, Csebisev-féle bizonyítást jobban szeretem, mert közelebb visz a prímszámtételhez). Ez egészen más tészta, mint egy megoldatlan probléma: Gauss vagy Erdős nem értették jobban az adott formulát, illetve tételt, mint mindenki más a világon; egy megoldatlan probléma megoldásához pedig éppen erre a mindenki másnál jobban értésre van szükség.
|
| Előzmény: [535] bily71, 2010-03-04 18:52:04 |
|
| [535] bily71 | 2010-03-04 18:52:04 |
 Amikor Gauss 9 évesen megtalálta a számtani sorozatok összegképletét vajon már matematikus volt, vagyis ismerte a vizsgált területet? Vagy Lovász esernyője? Erdős, és a Csebisev-tétel? Szerintem egy elemista, vagy egy specmatekos gimnazista semmiféleképp nem nevezhető még matematikusnak, bármily tehetséges is. Persze utána mindannyian elismert matematikusok lettek.
De, hagyjuk a filozófálást, a feladatra koncentráljunk! Azt mondtad írjam le, mire gondoltam. Nos? Leírtam, vélemény? Hiba van a gondolatmenetben? Vakon elfogadtad RG program-eredményét, vagy utánaszámoltál? Az igaz, hogy f(x) átalakítása nekem nem sikerült, de az eredeti alakjából nekem más jött ki. Hol hibáztam? A logikai szita nem enged harmadik lehetőséget, egy szám vagy tagja egy sorozatnak, vagy nem. Hogy lehetne már f(x) nagyobb x-nél, vagy negatív? Ha még mindig érdekel, leírom a részletes számolást, mondjuk n=10-re. Az is lehet, hogy nem a megfelelő jelöléseket használom. Most nem állítottam, hanem kérdést tettem föl: van-e felső korlátja f(x)-nek?
|
| Előzmény: [533] Maga Péter, 2010-03-04 15:26:54 |
|
| [534] agysejt | 2010-03-04 16:25:19 |
 Igen.
Kémiában is volt egy nagyon érdekes áttörés az utóbbi évtizedekben, semmi más nem volt a trükk, csak úgy szintetizáltak peptidet, hogy "összeöntötték" a fehérjéket: Matematika kombinatorika + biokémia = kombinatorikus kémia
|
| Előzmény: [533] Maga Péter, 2010-03-04 15:26:54 |
|
| [533] Maga Péter | 2010-03-04 15:26:54 |
 "Szóval van rá esély, hogy egy eredendően nem matematikus - aki 5 évig beássa magát egy adott tématerületbe - fog sikeresen megtámadni egy Milleniumi problémát."
Vagyis: egy eredendően nem matematikus sikeresen megtámad egy Milleniumi problémát -- miután matematikussá képezte magát. Nyilván minden egyéb tudományból, vagy akár a hétköznapi életből, vagy nagymama meséiből, akárhonnan szerzett ismeret, ötlet, elképzelés hasznos lehet, de voltaképp mindig arra lyukadunk ki, hogy meg kell ismerni a kutatni kívánt területet.
|
| Előzmény: [532] agysejt, 2010-03-04 14:58:50 |
|




 3nm
3nm n
n (i): Legyen k=6NM
(i): Legyen k=6NM



 (d) a Moebius-függvény, g(d) jelöli d legnagyobb prímosztoját, g(1)=1. Szedjük szét, és legyen
(d) a Moebius-függvény, g(d) jelöli d legnagyobb prímosztoját, g(1)=1. Szedjük szét, és legyen  s
s C:
C:  (s)=0, Re(s)>1/2+1/x, |Im(s)|=t}}.
(s)=0, Re(s)>1/2+1/x, |Im(s)|=t}}. .) Most azt kell meggondolni, hogy R(x) korlátos-e. Ha nem, akkor igaz a Riemann-sejtés.
.) Most azt kell meggondolni, hogy R(x) korlátos-e. Ha nem, akkor igaz a Riemann-sejtés.  bn, tehát f(xn)=m.".
bn, tehát f(xn)=m.".