|
| [913] Zilberbach | 2010-09-11 08:56:10 |
 Kedves Alma (és lgdt)!
Tartok tőle hogy az a lépés amit említessz visszafelé történt.
Sajnos az lgdt által írt képletet nem értem.
Ez az én hibám: csak egy régi, nem matematika tagozatos érettségim van, kb. ennek megfelelő tudással.
(Ezért csak megérzés alapján, egy hasonlat, amit erről írni tudok:
Bemegy a vevő az autó és motor szalonba, és egy olyan járművet kér ami megy 220 km/ó fölött. Erre mutatnak neki egy lábbal tekerős háromkerekű biciklit, amire rá van szerelve egy 240 km/ó végkitérésű sebességmérő műszer.)
Fölmerült viszont egy újabb gond a számomra a páros Goldbach sejtés bizonyításával kapcsolatban:
Tegyük föl, hogy van egy olyan képlet/megállapítás ami pontosan, egyszerűen, és matematikailag jól kezelhető formában megadja, mi a szabályszerűség az egymást követő prímszámok közötti különbség értékében, tehát a prímszámok előállnak, mint egy jól kezelhető sorozat. (Egyébként ez az ami szerintem nem így van, de most tételezzük föl.)
Lehet hogy még ez is kevés lenne a páros Goldbach sejtés bizonyításához, mert nem ismerjük (eléggé) milyen szabályok érvényesek a páros számok két prímszámra bontásánál. Úgy tudom, még sejtéseink sincsenek róla, azon túl hogy ez mindig lehetséges.
A páratlan számok 3 db. prímszámra bontásakor évényes szabályokra viszont jónéhány pontos és éles sejtés/bizonyítás van.
(Ezek közül a páros Goldbach-sejtés szempontjából a legfontosabb talán az a sejtés, hogy mindíg megoldható a páratlan szám három db. prímszámra bontásánál, hogy az egyik szám a 3 legyen. Ha ezt sikerülne bizonyítani, azzal már a páros Golbach-sejtés is bizonyítva lenne.)
|
| Előzmény: [910] Alma, 2010-09-10 19:57:16 |
|
| [912] Fernando | 2010-09-11 07:55:13 |
 Ha jól értem Zilberbach egy olyan formulára gondolt, hogy p=f(n) , ami sorban minden természetes n-re adja az n-dik prímet, vagy legalábbis prímet ad.
A Goldbach-sejtés bizonyításához sztem nemigen van szükség ilyen erős eszközre, persze ha lenne ilyen formulánk...
|
|
|
| [910] Alma | 2010-09-10 19:57:16 |
 Kedves Zilberbach!
Innen már csak egy lépés egy olyan függvény, amely minden prím helyén 1-et vesz fel, minden nem prím egész helyén pedig 0-át. Ez már megadja, hogy "pontosan hol vannak a számegyenesen"?
|
| Előzmény: [909] Zilberbach, 2010-09-10 19:45:09 |
|
| [909] Zilberbach | 2010-09-10 19:45:09 |
 Kedves Tibixe!
Nagyon féreértetted amit írtam.
Nem az a kérdés hányan vannak a prímszámok egy 2-től x-ig terjedő tartományban, hanem az hogy: kik ők, és pontosan hol vannak a számegyenesen (- ami jelen esetben ugyanaz).
|
| Előzmény: [908] Tibixe, 2010-09-10 19:17:28 |
|
| [908] Tibixe | 2010-09-10 19:17:28 |
 ,,megadná, hogy mi a pontos szabályszerűség a prímszámok elhelyezkedésére a számegyenesen''
Ja, csak ennyi a gondod? Ha a  (x) az x-nél kisebb prímek száma, akkor (x) az x-nél kisebb prímek száma, akkor

ahol

És ez nem közelítés, hanem pontos szabályszerűség.
|
| Előzmény: [907] Zilberbach, 2010-09-10 13:59:29 |
|
| [907] Zilberbach | 2010-09-10 13:59:29 |
 Kedves lgdt!
"De nem tudjuk a pontos elhelyezkedésüket megadni a számegyenesen a végtelenig."
Még mindig nem értem, hogy ez a mondat mit jelent.
Valószínűleg igazad van, az idézett mondatom nem világos, megpróbálom elmagyarázni:
Ha a páros számokat ábrázoljuk a számegyenesen akkor pontokat kapunk 2-nél, 4-nél, 6-nál, 8-nál ... és így tovább. Valahol a papírnak vége van, de simán extrapoláljuk - fejben is - hogy a további részben minden második természetes szám ponttal lesz jelölve. Egy könnyen kezelhető képlettel is fölírhatjuk, nem muszály ábrázolnunk: páros szám = 2n, -ahol n bármely természetes szám, és n nem= 0. (Előzőleg azt kérted írjam le mit értek képleten)
Ha a prímszámok előforduását ábrázoljuk a számegyenesen, akkor pontokat kapunk 2-nél, 3-nál, 5-nél, 7-nél ... és így tovább. Valahol a papírnak itt is vége lesz, de ha nem ismerjük eleve a prímszámokat, intuiciónk nem lehet róla hogy melyik lesz a következő. Minden következő számot meg kell vizsgálni, hogy prímszám -e vagy sem, és csak így folytatódhat a prímszámok ábrázolása.
És nem tudom egy az előzőhöz hasonló képlettel megadni, hogy: prímszám = .....
"Olyan fekete dobozt szeretnél, amibe beadod, hogy hanyadik prímszámot szeretnéd, és kiköpi a prímszámot? Ilyen természetesen létezik."-írod.
Itt a Golbach-sejtés fórumban egy olyan fekete dobozt szeretnék, ami megadná, hogy mi a pontos szabályszerűség a prímszámok elhelyezkedésére a számegyenesen, mondjuk egy (lehetőleg majdnem hasonlóan egyszerű) képlettel (mint a páros szám = 2n, ahol n bármely természetes szám, de n nem= 0).
|
| Előzmény: [906] lgdt, 2010-09-10 11:49:27 |
|
| [906] lgdt | 2010-09-10 11:49:27 |
 "De nem tudjuk a pontos elhelyezkedésüket megadni a számegyenesen a végtelenig."
Még mindig nem értem, hogy ez a mondat mit jelent.
Olyan fekete dobozt szeretnél, amibe beadod, hogy hanyadik prímszámot szeretnéd, és kiköpi a prímszámot? Ilyen természetesen létezik.
Vagy olyat, aminek a bemenete egy szám, a kimenete pedig az, hogy az adott szám prímszám-e? Ilyen is létezik, ráadásul polinomiális futásidejű.
|
| Előzmény: [905] Zilberbach, 2010-09-10 07:20:32 |
|
| [905] Zilberbach | 2010-09-10 07:20:32 |
 Szinte mindenki félreértette a 2 pontomat, ezért ismételném magam egy kevésbé félreérthető formában.
Sokat tudunk a prímszámok elhelyezkedéséről a számegyenesen.
Tudjuk hogy végtelenül sok van, tudjuk hogy n és 2n között mindíg előfordul legalább egy, ismerjük a pontos elhelyezkedésüket a számegyenes egy viszonylag hosszú kezdeti szakaszán, és még sok ismeretet lehetne sorolni.
De nem tudjuk a pontos elhelyezkedésüket megadni a számegyenesen a végtelenig.
Az egyik állításom ez volt:
VALÓSZÍNŰ, hogy ez nem is lehetséges.
Az általunk megszerzett tudás - amennyiben Vinogradov bizonyítása jó, és ez majdnem biztos - elég ahhoz hogy bizonyítsuk: minden 5-nél nagyobb páratlan szám előállítható 3 prímszám összegeként.
A másik állításom:
LEHET hogy az általunk megszerezhető tudás a prímszámok elhelyezkedéséről a számegyenesen, kevés a páros Goldbach sejtés bizonyításához.
Mindkét állítás föltételes módban van, ezért inkább egy egy vizsgálandó kérdés, és nem egy kinyilatkoztatás, bár a "valószínű" és a "lehet" nem azonos értékű szavak.
|
|
|
| [903] Fernando | 2010-09-09 22:44:06 |
 Nos igen, könnyen lehet...
"mindkét sejtés bizonyításáoz szükséges volna egy képlet, ami megadná a prímszámok elhelyezkedését a számegyenesen, a 2-től a végtelenig"
sztem ez már eleve nem szükségszerű.
|
| Előzmény: [900] Zilberbach, 2010-09-08 20:21:55 |
|
| [902] Maga Péter | 2010-09-09 09:38:52 |
 Nnnnna...
az van, hogy azt nem érted, hogy egy ilyen képlet (bármit jelentsen is ez a szó) nemlétezésének vajmi kevés köze van a páros Goldbach bizonyíthatatlanságához.
Gondolj a páratlan Goldbachra! Van képlet? Nincs. Van bizonyítás? Van.
|
| Előzmény: [900] Zilberbach, 2010-09-08 20:21:55 |
|
|
| [900] Zilberbach | 2010-09-08 20:21:55 |
 Kedves Maga Péter!
Végtelen sok prímszám van, de nem tudjuk pontosan hol vannak (azok amiket még nem fedeztek föl).
Az 1. pontban említett képlet ahhoz kellene, hogy tudjuk hol vannak, pontosabban ahhoz, hogy kezelni tudjuk őket a matematika eszközeivel olyan szinten, hogy bizonyíthatóvá váljon a páros Goldbach sejtés.
Én elképzelhetőnek tartom, hogy enélkül a páros Goldbach sejtés nem bizonyítható, de könnyen lehet, hogy tévedek.
|
| Előzmény: [899] Maga Péter, 2010-09-08 12:51:51 |
|
|
| [898] Zilberbach | 2010-09-07 23:48:05 |
 Egy igen teoretikus, de egyszerű példa:
Ha valakinek sikerülne bizonyítania, hogy a bölcsek kövének előállításához feltétlenül szükség van kizárólag pozitronokból álló varjúhájra, majd utána valaki bizonyítaná hogy ilyen varjúhájat lehetetlen előállítani, akkor ezzzel a két bizonyítással egyúttal bizonyítaná azt is, hogy a bölcsek kövét nem lehet előállítani.
|
| Előzmény: [896] Fernando, 2010-09-07 22:07:58 |
|
|
| [896] Fernando | 2010-09-07 22:07:58 |
 Én most nem látom, hogy 1-esből és 2-esből együtt miért következne az, hogy lehetetlen bebizonyítani, mert ki mondja meg, hogy nincs valami egészen más útja a bizonyításnak...
|
| Előzmény: [895] Zilberbach, 2010-09-07 22:00:20 |
|
| [895] Zilberbach | 2010-09-07 22:00:20 |
 Kedves Fernando!
Sajnos attól messze vagyok, hogy le tudjam vezetni: lehetetlen a Goldbach sejtés bizonyítása.
Inkább csak egy vázlatát írtam meg, hogyan lehetne érzésem szerint bizonyítani a lehetetlenségét.
Sajnos én valószínűleg messze nem rendelkezem elég matematikai tudással és gyakorlattal, hogy ezt a program-vázlatot végre tudjam hajtani.
|
| Előzmény: [894] Fernando, 2010-09-07 20:46:43 |
|
| [894] Fernando | 2010-09-07 20:46:43 |
 Kedves Zilberbach!
Az 1. sok pénzt megérne. Ha lenne ilyenem, akkor én el nem árulnám, hanem időnként eladnék egy-egy prímet... :)
Nem értem, hogy miből vezetted le, hogy LEHETETLEN a bizonyítás.
|
| Előzmény: [891] Zilberbach, 2010-09-06 06:54:15 |
|
| [893] bily71 | 2010-09-06 16:50:14 |
 Akkor kifejtem bikicsunáj nyelven:)
Ha az általam kreált bites táblázat minden, a főátlóra merőleges kisátlójában van legalább egy darab 1-es, akkor igaz a Goldbach'.
Ha minden, a főátlóval párhuzamos mellékátlón van legalább egy darab 1-es, akkor igaz a "Zilberbach-sejtés".
Ha ugyanezen átlókon végtelen sok 1-es van, akkor igaz az ikerprím' és az általánosítása.
Az 1-esek számát szitamódszerekkel lehet becsülni, de ezek a módszerek kevésnek bizonyulnak.
|
| Előzmény: [886] Róbert Gida, 2010-09-05 22:51:12 |
|
|
| [891] Zilberbach | 2010-09-06 06:54:15 |
 Azért vetettem föl a fórumon a p-q=n kérdését, mert úgy érzem hasonló a páros Golbach sejtéshez, az alábbiakban:
1. Egy nálam műveltebb, és ötletesebb matematikus talán ki tudná mutatni, hogy mindkét sejtés bizonyításáoz szükséges volna egy képlet, ami megadná a prímszámok elhelyezkedését a számegyenesen, a 2-től a végtelenig.
2. Ez a nálam műveltebb, és ötletesebb matematikus válószínűleg be tudná bizonyítani azt is, hogy ilyen képlet nem létezhet.
Fönti két pontból együtt pedig az következik, hogy a két sejtés bizonyítása lehetetlen.
|
|
| [890] Róbert Gida | 2010-09-06 01:26:36 |
 q-p=2n-et írjunk inkább, ekkor q=p+2n, azaz p,p+2n prímek és k=1,a1=2n a sejtésben (itt most az n konstans, nem nulla). Így ez tényleg spec esete a sejtésnek, ami szerint így az ilyen párok száma aszimptotikusan p<x-ig 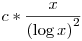 (wolframnál integrál van, az pontosabb). Ikerprímsejtés pedig pont az n=1 eset, hiszen ekkor p,p+2 prímek. (wolframnál integrál van, az pontosabb). Ikerprímsejtés pedig pont az n=1 eset, hiszen ekkor p,p+2 prímek.
Az általános sejtés pedig arról szól, hogy, ha a1,...ak különböző pozitív egészeket megadsz, melyekre 0,a1,...,ak semmilyen r prímre sem ad meg minden maradékot mod r (ez a trivi oszthatósági feltétel wolframnál), akkor végtelen sok p-re lesz p,p+a1,...,p+ak prím, és ezek száma p<x-ig aszimptotikusan 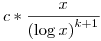 . Onnan is látható, hogy a sejtés valószínűleg igaz, hogy ugyanennyi megoldás van x-ig, ha a p,p+a1,...,p+ak számok egymástól függetlenül prímek, mert akkor egynek a valószínűsége . Onnan is látható, hogy a sejtés valószínűleg igaz, hogy ugyanennyi megoldás van x-ig, ha a p,p+a1,...,p+ak számok egymástól függetlenül prímek, mert akkor egynek a valószínűsége 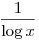 , de nekünk k+1 prím kell, és függetlenség miatt így , de nekünk k+1 prím kell, és függetlenség miatt így 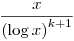 darab megoldás lesz. (Sejtésben konstans szorzó is van persze.) darab megoldás lesz. (Sejtésben konstans szorzó is van persze.)
k=0-ra egyébként ez a prímszámtétel (nincsenek a-k, csak p).
Ahhoz, hogy lásd, hogy kell az oszthatósági feltétel nézd meg, hogy például miért van véges sok p prím, melyre p,p+2,p+4 mindegyike prím.
Még annyit, hogy te gyengébbet kérdeztél, csak azt, hogy q-p=2n-nek minden n-re van-e megoldása, bár ez szerintem ugyanúgy megoldatlan és nem lehet sokkal *könnyebb*, mint a végtelenes verzió.
|
| Előzmény: [889] Zilberbach, 2010-09-06 00:14:01 |
|





 (n)-
(n)-




