| [583] Blord | 2010-04-16 14:58:57 |
 Még nem szóltam hozzá a topikhoz, de hosszú ideje szeretnék már. Matematikát tanulok, és a következő a problémám. Bármilyen matematikai szöveggel találkoztam eddig, ha koncentrációképes állapotban voltam, világosan értettem a gondolatmenetet, de inkább úgy kéne mondanom, minden esetben láttam, hogy a gondolatmenet értelmes. Kivétel nélkül. Ha a hozzászólásaidat olvasom, egyáltalán nem ez a helyzet, fejfájdítóan zavaros és követhetetlen gondolatmeneteket találok, ha ránézek egy mondatra, már káprázik a szemem. Abszolúte érthetetlen számomra, hogy mit, miért, hogyan csinálsz, továbbá azt sem értem, hogyan lehetsz ilyen mértékben kritikátlan: feltételezed, hogy új, friss, matekszűz aggyal esélyed van olyan problémákhoz érdemben hozzájárulni, melyeket mindkettőnk számára felfoghatatlan mértékben kifinomultan gondolkodó emberek hatalmas technikai képességekkel és óriási háttértudással is képtelenek voltak megoldani. Ráadásul nem egyszer történt ez a fórumon, hanem újra és újra, megállíthatatlanul írsz, mint valami Don Quijote, aki csakazértis nekimegy a malomnak. Nem jöttél rá, hogy a möbius, szumma, produktum jelölések használata, sőt gombamód szaporodása nem mély számelméleti problémákhoz való közelségről árulkodnak, hanem pusztán arról, hogy megszeretted ezeket a jelöléseket. Továbbá: "könnyen belátható", "végezze el, akinek több ideje van hozzá, mint nekem", "ha érdekel valakit, vegyen komolyan" (nem pontos idézetek) mind mind megengedhetetlenek valakitől, aki nem tett le semmit az asztalra. Grigori Perelman írhat ilyen egy arxiv-ra feltett cikkben, vagy Lackovich Miklós a tankönyvében, mikor két esetből egyet bizonyít, és a másikat pont így kell csinálni; más nem (nyilván nem csak ők ketten, a már bizonyított színvonalukról van szó).
Ezen felül, ami a legfurcsább: egyáltalán nem a matematika szeretete vezérel téged, hanem a vágyakozás arra az élményre, hogy megbirkózz a legnehezebbel, és mindenki azt mondja, hogy "DE OKOS VAGY!". Ezzel magyarázható az a tény, hogy előjel nélkül egyszer csak megjelentél, és győzedelmesen elkurjantottad magadat. Ezzel magyarázom azt, hogy nem óhajtod magadat kipróbálni kis zsákmányállatokon. Ezzel magyarázom azt, hogy minden egyes újonnan felfogott dolgot megpróbálsz felhasználni az újabb verziójú bizonyításokban, anélkül, hogy a mélyebb megértés szintjére eljutnál.
Teljesen fölösleges a kedvesség, megértés, biztatás az olyanokkal szemben, mint te (többet kaptál -és természetesen teljesen fölöslegesen- mint megérdemeltél), reménytelen eset vagy. Nem tudsz belegondolni abba, hogy sokezer ember ugyanazt csinálja szerte a világon, mint te: Hozzáértő, érdeklődő, kíváncsi embereket bombáz a fanatizmusával, és NEM ÉRTI MEG, hogy mi a probléma. Nem értik, hogy a tudomány demokratikussága nem azt jelenti, hogy minden vélemény egyből komoly odafigyelést, meggondolást érdemel. Nem látják be, hogy a puszta okosság, felületes érdeklődés szintje, és az aktív tudomány, nem beszélve az éltudomány szintje között micsoda elképesztő különbségek vannak. Nem akarnak szembesülni azzal, hogy mennyire klisés, és számtalanszor kipróbált ötletekkel akarnak diadalt aratni. Nem látják a törvényszerűségét annak, hogy a hozzá nem értő ember lényegében sohasem jeleskedhet a fanatizált szakterületen, mindegyikük kivételesnek látja pontosan saját magát.
Összességében két dologgal zárnám a hozzászólásomat. Először: nem volt jó érzés megírnom a fentieket, de a kellemes közérzet, és a békés (passzív) együttélés bizony sokszor ellentétben áll az őszinteséggel és az igazsággal. Másodszor: ne személyes támadásnak vedd a hozzászólást, de jót tennél magadnak, ha végre elgondolkodnál azon, hogy a hiba elsősorban nem ott van, hogy elhagytál elhagyhatatlan egészrészeket, de a 0.26-os Goldbach-verzióban már szó sincs ilyesmiről.
|
| Előzmény: [582] bily71, 2010-04-16 12:57:26 |
|
| [582] bily71 | 2010-04-16 12:57:26 |
 Csakhogy, most az egyszer nem az egészrészek elhagyására gondoltam...
Ha megvizsgáljuk a ![g_q(x)=\sum_{d|P(q)}\mu(d)\left[\frac{x}{d}\right]](keplet.cgi?k=B3FC4137BA3D7A0C) függvényeket, ahol függvényeket, ahol 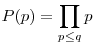 , (p,q prímek), azt fogjuk tapasztalni, hogy minden függvény 0-tól 1-ig a 0, 1-től a q után következő prímig az 1, és ennél a 2 értéket veszi fel, ugyanis x=q2-ig a függvény csak a prímeknél ugrik, kivéve a q és a nála kisebb prímeket, pontosan ezért kell korrigálni az összeget a , (p,q prímek), azt fogjuk tapasztalni, hogy minden függvény 0-tól 1-ig a 0, 1-től a q után következő prímig az 1, és ennél a 2 értéket veszi fel, ugyanis x=q2-ig a függvény csak a prímeknél ugrik, kivéve a q és a nála kisebb prímeket, pontosan ezért kell korrigálni az összeget a 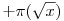 taggal. Tehát taggal. Tehát ![\sum_{d|P(\sqrt{x})}\mu(d)\left[\frac{x}{d}\right]+\pi(\sqrt{x})](keplet.cgi?k=7D22C4F1B618074C) nemkorlátossága úgy is belátható, hogy a fentebb leírt függvénysorozatot csak az x=q helyeken vizsgáljuk, hiszen ott mindig az 1 éréket veszi fel, ehhez meg mindig hozzá kell adni a kisebb prímek számát, így ezen a helyen mindig q lesz a felvett érték. Ez persze körkörös érvelés, hiszen tudjuk, hogy a prímek száma végtelen, és ezért nem korlátos a függvény. De hasonló módszerrel vizsgálható az nemkorlátossága úgy is belátható, hogy a fentebb leírt függvénysorozatot csak az x=q helyeken vizsgáljuk, hiszen ott mindig az 1 éréket veszi fel, ehhez meg mindig hozzá kell adni a kisebb prímek számát, így ezen a helyen mindig q lesz a felvett érték. Ez persze körkörös érvelés, hiszen tudjuk, hogy a prímek száma végtelen, és ezért nem korlátos a függvény. De hasonló módszerrel vizsgálható az ![f(x)=\sum_{d|P_q(\sqrt{x})}\nu_a(d)\left[\frac{x}{d}\right]+n](keplet.cgi?k=DA82E6E136A9A2E6) függvénycsalád is, mert elég azt belátni, hogy a függvénycsalád is, mert elég azt belátni, hogy a ![g_q(x)=\sum_{d|P(q)}\nu_a(d)\left[\frac{x}{d}\right]](keplet.cgi?k=857F5DB615AE3A2C) függvény sorozat az x=q helyeken, vagyis, amikor x egyenlő a szitában lévő legnagyobb prímmel, nem vehet fel kisebb értéket, mint az előző függvény az ő legnagyobb prímjével egyenlő helyen. függvény sorozat az x=q helyeken, vagyis, amikor x egyenlő a szitában lévő legnagyobb prímmel, nem vehet fel kisebb értéket, mint az előző függvény az ő legnagyobb prímjével egyenlő helyen.
Egyébként a kifogásolt egyenlőtlenség is belátható oly módon, ha megkeressük ![\prod_{q\le{p}}\left(1-\frac1p\right) < \sum_{d|P(q)}\mu(d)\left[\frac{x}{d}\right]](keplet.cgi?k=53D9772FDBF14B29) a jobb és baloldal között hol a legnagyobba különbség. Mivel a jobb oldalon lévő függvénysorozat periódikus, és szimmetrikus, de nem a megszokott értelemben, és 1-től r-ig az 1 értéket veszi fel, (r a q után következő prím), (itt a függvény képe egy r-1 hosszúságú szakasz), ezért a jobb és baloldal között hol a legnagyobba különbség. Mivel a jobb oldalon lévő függvénysorozat periódikus, és szimmetrikus, de nem a megszokott értelemben, és 1-től r-ig az 1 értéket veszi fel, (r a q után következő prím), (itt a függvény képe egy r-1 hosszúságú szakasz), ezért 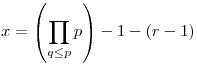 -től -től 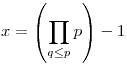 -ig is egyenlő értékeket fog felvenni, méghozzá a -ig is egyenlő értékeket fog felvenni, méghozzá a 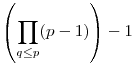 -et. Ha összekötjük ezeket a pontokat, és vesszük a -et. Ha összekötjük ezeket a pontokat, és vesszük a ![h(x)=\left[(x+a)\prod_{q\le{p}}\left(1-\frac1p\right)\right]](keplet.cgi?k=F0093A34A35DF5C5) egyenes egészrészfüggvényét, (a pozitív racionális, értéke kiszámítható) a jobb oldal, és az egyenes egészrészei közötti eltérés nem lehet nagyobb, mint n, vagyis a szitában lévő prímek száma. Az, hogy hol és mennyi az eltérés pontosan azonosítható, ezáltal belátható, hogy h(x) jobban közelíti a jobboldalt, mint a baloldal. De ez Téged úgysem érdekel, de hátha másokat... egyenes egészrészfüggvényét, (a pozitív racionális, értéke kiszámítható) a jobb oldal, és az egyenes egészrészei közötti eltérés nem lehet nagyobb, mint n, vagyis a szitában lévő prímek száma. Az, hogy hol és mennyi az eltérés pontosan azonosítható, ezáltal belátható, hogy h(x) jobban közelíti a jobboldalt, mint a baloldal. De ez Téged úgysem érdekel, de hátha másokat...
|
| Előzmény: [581] Maga Péter, 2010-04-16 10:16:07 |
|
| [581] Maga Péter | 2010-04-16 10:16:07 |
 Én ennek nem sok értelmét látom. Meg vagyok róla győződve, hogy ez a próbálkozás (is) kudarcot fog vallani. Már régen nem az érdeklődés beszél belőlem, hanem az a szándék, hogy erről a hiábavaló időpazarlásról lebeszéljelek. Sajnálom, hogy ha ezt a szándékomat félreértetted, és nem szűnő hozzászólásaimat az érdeklődés jelének tekintetted. Igen, a matematikai tartalomra is reagáltam: ha sokadszorra is az a becslés lelke, hogy elhagytad az egészrészeket, akkor sokadszorra is leírtam, hogy ez a becslés nagyon pontatlan. A Tao-féle irányelvből sem véletlenül emeltem ki azt a mondatot, amit: ha nem tökéletes elsőre, nem foglalkozik tovább vele. Hányszorosan léptük már túl ezt a korlátot?
Érdekel a matematika? Ott vannak az érdekes matekfeladatok, az ujjgyakorlatok, a nehezebb matematikai problémák, a lejárt határidejű KöMaL-feladatok a megfelelő témákban.
|
| Előzmény: [580] bily71, 2010-04-16 09:28:35 |
|
| [580] bily71 | 2010-04-16 09:28:35 |
 Reméltem, hogy az összegzésem jó, hisz az "józan paraszti ésszel is belátható", különösebb bizonyítást nem igényel.
Az n tag, mintmár leírtam, a 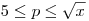 közé eső prímek száma. Miért adjuk hozzá az összegzéshez? Mert a (6n közé eső prímek száma. Miért adjuk hozzá az összegzéshez? Mert a (6n 1)(6m 1)(6m 1) szorzatokban n,m>0, így azok az n(6m 1) szorzatokban n,m>0, így azok az n(6m )+m alakú számok, ahol n=0 nem szerepelnek ezen számokból képzett szorzótábla megfelelő soraibanban, de a szita számol velük. Hogy világosabb legyen: van két sorozatunk, amelyek difije 5. A kezőtagok 5.1-1=5.0+4=4 és 5.1+1=6. A szita pedig olyan sorozatokat rostál, amelyek kezdőtagjai 5.0+1=1 és 5.0+4=4. Tehát módosítani kell az eredméyt, ugyanúgy, mint a prímek esetén a Legendre-formulában lévő összegzéshez is hozzáadjuk n-t, vagyis a )+m alakú számok, ahol n=0 nem szerepelnek ezen számokból képzett szorzótábla megfelelő soraibanban, de a szita számol velük. Hogy világosabb legyen: van két sorozatunk, amelyek difije 5. A kezőtagok 5.1-1=5.0+4=4 és 5.1+1=6. A szita pedig olyan sorozatokat rostál, amelyek kezdőtagjai 5.0+1=1 és 5.0+4=4. Tehát módosítani kell az eredméyt, ugyanúgy, mint a prímek esetén a Legendre-formulában lévő összegzéshez is hozzáadjuk n-t, vagyis a 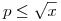 prímek számát, amik tulajdonképp a sorozatok kezdőtagjai, hasonlóan a mostani számoláshoz, ahol, ha egymásba toljuk a két sorozatot, ezen számok szintén a sorozatok kezdő tagjai. prímek számát, amik tulajdonképp a sorozatok kezdőtagjai, hasonlóan a mostani számoláshoz, ahol, ha egymásba toljuk a két sorozatot, ezen számok szintén a sorozatok kezdő tagjai.
Ha elhagyjuk az egészrészeket valóban reménytelennek tűnik az alsó becslés, hiszen minden új prímmel megduplázódik a szitában lévő tagok száma. De azért vannak törvényszerűségek, melyeket figyelembe vehetünk, pl. az ilyen függvény azokon a helyeken ugrik , ahol x egész értéket vesz fel, és nem oszható a szitában szereplő prímek egyikével sem, ahol osztható, ott lefelé is ugorhat. Ha p a szitában lévő legkisebb prím, azokon a helyeken is ugorhat a függvény, ahol x a p-nél kisebb prímek többszöröse. Mint írtam, van errevonatkozólag javaslatom, és úgy látom van (személyedben) legalább egy érdeklődő, ezért közzéteszem, de később, most nincs időm.
|
| Előzmény: [578] Maga Péter, 2010-04-15 22:21:55 |
|
| [579] Maga Péter | 2010-04-15 22:24:33 |
 A saját irányelveit ismerteti. Engem az a mondat fogott meg, hogy: "I will not consider any further revisions or resubmissions beyond the first when it comes to these sorts of submissions; it has to be perfect the first time, or it will not be considered at all."
|
| Előzmény: [577] bily71, 2010-04-15 20:37:50 |
|
| [578] Maga Péter | 2010-04-15 22:21:55 |
 A "Bizonyítható a következő reláció" kezdetű rész számomra nem világos, márpedig a kutya ott van elásva: megint arról van szó, hogy rengeteg egészrészt elhagytunk, nemigen lehet tudni, alsó becslés adódik-e vele. Már sokadszor szaladsz bele ugyanabba (a hibába). Másrészt a végső, f(x)-re adódó formulában van egy +n, amiről fogalmam sincs, mit jelent.
|
| Előzmény: [574] bily71, 2010-04-15 14:48:21 |
|
| [577] bily71 | 2010-04-15 20:37:50 |
 Valami olyasmiről van szó, hogy milyen irányelveket kövessen egy szerkesztő az ilyen irományok véleményezése kapcsán?
Szerintem a legjobb irányelv elolvasni és elgondolkozni rajta, persze csak akkor, ha valakit éredekel. Én a Te és a többiek konkrét véleményére vagyok kiváncsi. Legfőképp arra, hogy hol a hiba?
Tudom, hogy egy precíz bizonyításhoz ez nagyon messze van, de ha az ötlet jó, igazi szakértőknek semmeddig sem tart átfogalmazni, kiegészíteni.
|
| Előzmény: [575] Maga Péter, 2010-04-15 19:16:12 |
|
| [576] bily71 | 2010-04-15 20:06:08 |
 Bevallom öszintén, hogy az angol nyelvtudásom inkább a hétköznapi csevegésre szorítkozik, az ilyen bonyolult, tudományos szövegekből nem mindent értek, a sejtések, problémák nevét azért még felismertem:).
Felvázolnád nagyvonalakban, hogy mi a lényege?
|
| Előzmény: [575] Maga Péter, 2010-04-15 19:16:12 |
|
| [575] Maga Péter | 2010-04-15 19:16:12 |
 Olvassuk el ezen lapnak az Editorial policy on submissions concerning famous problems című részét.
|
|
| [574] bily71 | 2010-04-15 14:48:21 |
 Ha elhagyjuk a
![\sum_{d|P_q(\sqrt{x}}\nu_a(d)\left[\frac{x}{d}\right]](keplet.cgi?k=B1DC437DDF5A33FB)
összegzésben szereplő egészrészjeleket, akkor a következőt kapjuk
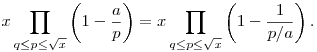
Bizonyítható a következő reláció
![x\prod_{q\le{p}\le\sqrt{x}}\left(1-\frac{1}{p/a}\right)<\sum_{d|P_q(\sqrt{x})}\nu_a(d)\left[\frac{x}{d}\right].](keplet.cgi?k=667686106EB17B91)
a=2 és q=5 esetén
![x\prod_{5\le{p}\le\sqrt{x}}\left(1-\frac{1}{p/2}\right)<\sum_{d|P_5(\sqrt{x})}\nu_2(d)\left[\frac{x}{d}\right].](keplet.cgi?k=B8A4C0911E551DB4)
Mivel a baloldal nem korlátos, a jobb sem lehet az. Vagyis végtelen sok pozitív egész nem áll elő 6nm n n m alakban. Ezek száma x-ig m alakban. Ezek száma x-ig
![f(x)=\sum_{d|P_5(\sqrt{x})}\nu_2(d)\left[\frac{x}{d}\right]+n,](keplet.cgi?k=C59B3609FEABD54C)
ami egészen pontosan azt jelenti, hogy, ha f(x) az x helyen az y értéket veszi fel, akkor 6[x]-ig az ikerprímpárok száma y.
Q.E.D.
Ha jó a bizonyításom, (amiben erősen kételkedem), akkor közzéteszem a p,p+4 prímpárok számára vonatkozó bizonyítási javaslatomat. Ha nem jó, nyugodtan állítsatok le, mielőtt még tovább mennék, semmi kedvem újfent hülyét csinálni magamból:)
|
| Előzmény: [573] bily71, 2010-04-14 23:35:42 |
|
| [573] bily71 | 2010-04-14 23:35:42 |
 Az ikerprím-sejtés ekvivalens azzal a sejtéssel, hogy végtelen sok olyan pozitív egész van, amely nem tagja a 6m 1 alakú prímekhez rendelt n(6m 1 alakú prímekhez rendelt n(6m 1)-m és n(6m 1)-m és n(6m 1)+m sorozatok közül egyiknek sem, ahol n végigfut a természetes számokon. (Ezt már tudjuk, nem írom le, hogy miért). A sorozatok kezdő tagjai a prím egyhatodának alsó, vagy felső egészrésze és ennek -1-szerese modulo p, (ha 6m+1 alakú, akkor alsó, ha 6m-1 alakú, akkor felső, vagyis m és p-m, de lehetnének bármely különböző maradékosztályok). 1)+m sorozatok közül egyiknek sem, ahol n végigfut a természetes számokon. (Ezt már tudjuk, nem írom le, hogy miért). A sorozatok kezdő tagjai a prím egyhatodának alsó, vagy felső egészrésze és ennek -1-szerese modulo p, (ha 6m+1 alakú, akkor alsó, ha 6m-1 alakú, akkor felső, vagyis m és p-m, de lehetnének bármely különböző maradékosztályok).
Jelölje f(x) azon egészek számát, melyek x-ig nem tagjai egyik sorozatnak sem. Ekkor, az előző hozzászólásokban részletzezett okok miatt
![f(x)=\sum_{d|P_5(\sqrt{x})}\nu_2(d)\left[\frac{x}{d}\right]+n,](keplet.cgi?k=C59B3609FEABD54C)
ahol n azon prímek száma, melyekre teljesül, hogy 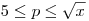 , vagyis n= , vagyis n= (x)-2. Azért adjuk hozzá az összeghez n-t, mert m valójában nem tagja a sorozatoknak, (azért nem, mert nem szerepel ama táblázatban, ezt sem részletezem). (x)-2. Azért adjuk hozzá az összeghez n-t, mert m valójában nem tagja a sorozatoknak, (azért nem, mert nem szerepel ama táblázatban, ezt sem részletezem).
Következő lépésként meg fogjuk mutatni, hogy f(x) nem lehet korlátos.
Folyt. köv.
|
| Előzmény: [572] bily71, 2010-04-14 16:45:00 |
|
| [572] bily71 | 2010-04-14 16:45:00 |
 Mutassuk meg a 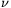 függvény létjogosultságát. függvény létjogosultságát.
Képezzünk véges sok számtani sorozatot, amelyek differenciái különböző prímek, és kezdőtagjuk a differencia valamely maradékosztályának a legkisebb eleme, vagyis a maradékosztályt reprezentáló pozitív egész. Ekkor, azon egészek számát x-ig, amelyek egyik sorozatnak sem tagjai a jól ismert logikai szita segítségével adhatjuk meg, vagyis az
![\sum_{d|P}\mu(d)\left[\frac{x}{d}\right]=\sum_{d|P}\nu_1(d)\left[\frac{x}{d}\right]](keplet.cgi?k=F18D142D2D247850)
összegzéssel, ahol P a differenciák szorzata.
Ugyanezen módon számoljuk ki a prímek számát x-ig, csak itt minden sorozat kezdő tagja maga a prím, és annyi sorozatot képzünk, ahány 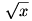 -nél kisebb, vagy egyenlő prím van. Mivel a szita csak a prímekkel nem osztható egészeket számolja, magukat a prímeket kihagyja az összegzésből, hiszen minden prím osztható önmagával, ezért az összeghez hozzáadunk annyi prímet, ahánnyal szitáltunk, aztán kivonunk egyet, mert az nem prím, de a szita annak veszi, mivel nem osztható egy prímmel sem. -nél kisebb, vagy egyenlő prím van. Mivel a szita csak a prímekkel nem osztható egészeket számolja, magukat a prímeket kihagyja az összegzésből, hiszen minden prím osztható önmagával, ezért az összeghez hozzáadunk annyi prímet, ahánnyal szitáltunk, aztán kivonunk egyet, mert az nem prím, de a szita annak veszi, mivel nem osztható egy prímmel sem.
Most pedig képezzünk véges sok, prím differenciájú számtani sorozatot úgy, hogy egy differenciához két sorozat tartozzon, úgy, hogy a két sorozat kezdőtagja a differencia valamely két különböző maradékosztályának legkisebb pozitív eleme.
Jelölje a prímeket pn, a két kezdőtagot un és vn. Ekkor a p1-hez rendelt első két sorozat x-ig ![2\left[\frac{x}{p_1}\right]](keplet.cgi?k=ACBE93341E16A14D) egészt tartalmaz. A p2-höz rendelt két sorozatban egészt tartalmaz. A p2-höz rendelt két sorozatban ![\left[\frac{x}{p_2}\right]](keplet.cgi?k=3E773DCA107406F5) egész található, de, mivel az u2+kp2 sorozat minden p1-dik tagja u1+kp1 alakú és ugyancsak minden p1-dik tagja v1+kp1 alakú és ugyanez elmondható a v2+kp2 sorozatról is, ezért egész található, de, mivel az u2+kp2 sorozat minden p1-dik tagja u1+kp1 alakú és ugyancsak minden p1-dik tagja v1+kp1 alakú és ugyanez elmondható a v2+kp2 sorozatról is, ezért ![4\left[\frac{x}{p_1p_2}\right]](keplet.cgi?k=32E214C463AFEC4F) darab egész megtalálható a P1-hez rendelt két sorozatban is. Ha folytajuk az eljárást, azt kapjuk, hogy azon egészek száma, amelyek nem szerepelnek egyik sorozatban sem szerepelnek darab egész megtalálható a P1-hez rendelt két sorozatban is. Ha folytajuk az eljárást, azt kapjuk, hogy azon egészek száma, amelyek nem szerepelnek egyik sorozatban sem szerepelnek
![[x]-2\left[\frac{x}{p_1}\right]-2\left[\frac{x}{p_2}\right]-...+4\left[\frac{x}{p_1p_2}\right]+4\left[\frac{x}{p_2p_3}\right]+...-8\left[\frac{x}{p_1p_2p_3}\right]=\sum_{d|P}\nu_2(d)\left[\frac{x}{d}\right],](keplet.cgi?k=90A566F24B749DC6)
ahol, ha d négyzetmentes, akkor 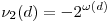 , ha nem négyzetmentes, akkor , ha nem négyzetmentes, akkor 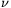 2(d)=0, 2(d)=0,  (d) d különböző prímsztóinak a száma. Az eljárást folytatva könnyen belátható, hogy, ha minden a-nál nagyobb prímhez a darab sorozatot rendelünk, akkor a sorozatokból kimaradó egészek száma x-ig (d) d különböző prímsztóinak a száma. Az eljárást folytatva könnyen belátható, hogy, ha minden a-nál nagyobb prímhez a darab sorozatot rendelünk, akkor a sorozatokból kimaradó egészek száma x-ig
![\sum_{d|P}\nu_a(d)\left[\frac{x}{d}\right],](keplet.cgi?k=AB7E7EA00C5411B4)
ahol 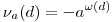 , ha d nem négyzetmentes, akkor , ha d nem négyzetmentes, akkor 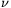 a(d)=0. a(d)=0.
Folyt. köv.
|
| Előzmény: [571] bily71, 2010-04-13 23:03:46 |
|
| [571] bily71 | 2010-04-13 23:03:46 |
 "...akkor a te f-függvényed nemkorlátossága nem lehet triviális. Vagyis kell lennie valami--könnyen, vagy nehezen megfogalmazható-- ötletnek..."
Nos van ötletem, úgy néz ki nem triviális, de az is lehet, hogy "halálismert".
Rájöttem, hogy a Moebius-függvény miért pont azokat az értékeket veszi fel, amit felvesz. Újra definiáltam, és így egy új függvénycsaládot kaptam, melynek első tagja a Moebius-függvény, és sikerült végre kirostálni a pozitív egészekből azokat, melyek nem állnak elő 6nm n n m alakban. m alakban.
Vezessük be a következő függvényt:
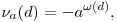
ahol a és d pozitív egészek,  (d) d különböző prímosztóinak a száma, ha d nem négyzetmentes, akkor (d) d különböző prímosztóinak a száma, ha d nem négyzetmentes, akkor 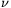 (d)=0. Ha a=1, akkor a Moebius-függvéy (d)=0. Ha a=1, akkor a Moebius-függvéy  (d)= (d)=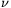 1(d). 1(d).
De, honnan jön a értéke? Amikor a prímeket számoljuk x-ig, akkor azt ulajdonképp azt vizsgáljuk, hogy hány olyan egész van x-ig, hogy a 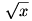 -nél kisebbegyenlő prímekhez rendelt számtani sorozatok egyikében sem szerepel. Ebben az esetben minden prímhez egy, olyan számtani sorozatot rendelünk, amelynek kezdő tagja maga a prím, és a differencia is maga a prím, ezért a sorozat minden tagja 0 modulo p. A prímek bármely maradékosztálya lehet kezdő tag, és lehet minden prím esetében más is, a Legendre-formula akkor is ugyanazt az eredményt fogja produkálni. -nél kisebbegyenlő prímekhez rendelt számtani sorozatok egyikében sem szerepel. Ebben az esetben minden prímhez egy, olyan számtani sorozatot rendelünk, amelynek kezdő tagja maga a prím, és a differencia is maga a prím, ezért a sorozat minden tagja 0 modulo p. A prímek bármely maradékosztálya lehet kezdő tag, és lehet minden prím esetében más is, a Legendre-formula akkor is ugyanazt az eredményt fogja produkálni.
Az ikerprímek esetében olyan számokat keresünk, melyek ugyancsak prímekhez rendelt számtani sorozatokból hiányoznak, de itt minden prímhez két sorozatot rendelünk. Tehát a értéke azt mutatja, hogy a szitában egy prímhez hány sorozatot rendelünk.
Jelölje f(x) azon egészek számát, amelyek nem állnak elő 6nm n n m alakban, ekkor m alakban, ekkor
![f(x)=\sum_{d|P_5(\sqrt{x})}\nu_2(d)\left[\frac{x}{d}\right]+\pi(\sqrt{x})-2,](keplet.cgi?k=DA3AACC44B676296)
ahol 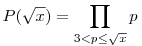 , vagyis, az 5 és a nála nagyobb, de , vagyis, az 5 és a nála nagyobb, de 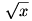 -nél kisebbegyenlő prímek szorzata. -nél kisebbegyenlő prímek szorzata.
Ha a 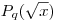 osztóival szitálunk és q>a, akkor osztóival szitálunk és q>a, akkor ![g(x)=\sum_{d|P_q(\sqrt{x})}\nu_a(d)\left[\frac{x}{d}\right]](keplet.cgi?k=FBC17042FE286049) sosem lesz korlátos, ezért f(x) sem lehet az. Természetesen, az előbbire van bizonyítási javaslatom. Továbbá a sejtésem az, hogy ez a módszer nemcsak az ikerprímek esetében használható, hanem bármely prímpárok esetében, melyek különbsége 2k. sosem lesz korlátos, ezért f(x) sem lehet az. Természetesen, az előbbire van bizonyítási javaslatom. Továbbá a sejtésem az, hogy ez a módszer nemcsak az ikerprímek esetében használható, hanem bármely prímpárok esetében, melyek különbsége 2k.
|
| Előzmény: [511] Maga Péter, 2010-03-01 10:07:19 |
|
| [570] bily71 | 2010-03-25 17:25:42 |
 Hát, persze, hogy nem világos! Rájöttem, hogy hol a hiba. Ez a szita nem azonos a logikai szitával. A sokadszorra javított levezetést elküldtem email-ben, remélem ez már érterhető lesz.
|
| Előzmény: [567] Maga Péter, 2010-03-19 17:26:23 |
|
|
|
|
| [566] bily71 | 2010-03-19 10:16:00 |
 A két oldal különbsége nem lehet korlátos, nem ezzel van gondom, ezt nem nehéz megmutatni. A kérdés itt igazából (számomra) az, hogy
![\sum_{d|P(p_n)}\mu(d)\left[\frac{p_n^2-(g(d))^2}{3d}\right]-\frac{n}2>\frac{p_n^2-1}{6},](keplet.cgi?k=9BBF8CC3104B4E02)
teljesül-e mert akkor tényleg kész vagyunk.
|
| Előzmény: [565] Maga Péter, 2010-03-19 09:24:38 |
|
| [565] Maga Péter | 2010-03-19 09:24:38 |
 Az utolsó kérdésre tudok válaszolni.
"Minél nagyobb n, a szita annál több szám ismétlődését nem veszi figyelembe, vagyis ha n nagy, akkor f3(x)<#3k 3nm 3nm n n m,0<k m,0<k x|k x|k N." Egyrészt ez kézlengetés: olyan, mintha úgy bizonyítanál, hogy hát végtelen sok prím van, elég szabálytalan hézagokkal, úgyhogy az a hézag végtelen sokszor 2. Másrészt, ha az egyenlőtlenségedben tényleg < áll fenn egy idő után mindig, attól még lehet, hogy a két oldal különbsége korlátos. És ekkor nem vagy kész. Mi van, ha a jobb oldal=bal oldal+43, ha x elég nagy? N." Egyrészt ez kézlengetés: olyan, mintha úgy bizonyítanál, hogy hát végtelen sok prím van, elég szabálytalan hézagokkal, úgyhogy az a hézag végtelen sokszor 2. Másrészt, ha az egyenlőtlenségedben tényleg < áll fenn egy idő után mindig, attól még lehet, hogy a két oldal különbsége korlátos. És ekkor nem vagy kész. Mi van, ha a jobb oldal=bal oldal+43, ha x elég nagy?
Felette a számolást nem néztem végig, de ebben biztosan tévedtél (lehet, hogy máshol is).
|
| Előzmény: [562] bily71, 2010-03-18 12:56:42 |
|
|
|
| [562] bily71 | 2010-03-18 12:56:42 |
 Azt kapjuk, hogy, ha k=3nm n n m és n,m párosak, akkor 2|k. m és n,m párosak, akkor 2|k.
Minden p>3 prím 3k 1 alakú, ahol 2|k. Tehát, ha a 6l 1 alakú, ahol 2|k. Tehát, ha a 6l 1 alakú számokból szórzótáblát csinálunk, és a táblázatba a 1 alakú számokból szórzótáblát csinálunk, és a táblázatba a ![\left[\frac{6l\pm1}{3}\right]](keplet.cgi?k=2584A8948AB06B83) értékét írjuk be, akkor a táblázatban csak a párosak szerepelnek. Ha a (3n értékét írjuk be, akkor a táblázatban csak a párosak szerepelnek. Ha a (3n 1)(3m 1)(3m 1)=3k 1)=3k 1 alakú számok szorzótáblájából elhagyjuk azokat a sorokat és oszlopokat, ahol n,m páratlanok, akkor az előbbivel azonos táblázatot kapunk. 1 alakú számok szorzótáblájából elhagyjuk azokat a sorokat és oszlopokat, ahol n,m páratlanok, akkor az előbbivel azonos táblázatot kapunk.
Tehát, f3(x) #{k #{k 3nm 3nm n n m,0<k m,0<k x|k x|k N} , ha N} , ha 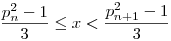 , akkor , akkor
![f_3(x)=2\sum_{d|P(p_n)}\mu(d)\left[\frac{p_n^2-(g(d))^2}{3d}\right]-n-\frac{p_n^2-1}{3},](keplet.cgi?k=DADF0C6008705C74) | (1) |
ahol 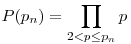 , g(d) d legnagyobb prímosztója, g(1)=1. , g(d) d legnagyobb prímosztója, g(1)=1.
Legyen
![h(x)=-\sum_{d|P(p_n),d>1}\mu(d)\left[\frac{p_n^2-(g(d))^2}{3d}\right]+n.](keplet.cgi?k=08E67457E2C97E88) | (2) |
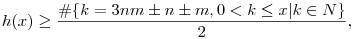 | (3) |
vagyis h(x) nagyobbegyenlő, mint a táblázatban szereplő különböző számok számának fele, vagyis az 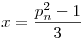 helyeken helyeken
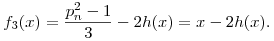 | (4) |
Ebből
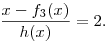 | (5) |
Mivel legalább egy ikerprím létezik, ezért két eset lehetséges:
(i) 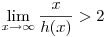 , ez esetben f3(x) , ez esetben f3(x)  és mivel és mivel 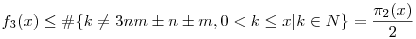 , ezért , ezért  2(x) nem korlátos. 2(x) nem korlátos.
(ii) 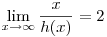 , ez esetben f3(x) korlátos. Az f3(x) , ez esetben f3(x) korlátos. Az f3(x) {K {K 3nm 3nm n n m,0<k m,0<k x|k x|k N} egyenlőség csak kis n-ekre igaz. Minél nagyobb n, a szita annál több szám ismétlődését nem veszi figyelembe, vagyis ha n nagy, akkor f3(x)<#{3k N} egyenlőség csak kis n-ekre igaz. Minél nagyobb n, a szita annál több szám ismétlődését nem veszi figyelembe, vagyis ha n nagy, akkor f3(x)<#{3k 3nm 3nm n n m,0<k m,0<k x|k x|k N}. N}.
Ebből következik, hogy 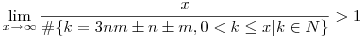 , tehát , tehát  2(x) nem korlátos. 2(x) nem korlátos.
Ez így túl egyszerű, hol tévedtem?
|
| Előzmény: [557] Maga Péter, 2010-03-07 23:18:24 |
|
| [561] Maga Péter | 2010-03-15 18:57:38 |
 Azért ha van hozzá kedv, akkor csinálhatnánk valami épületeset is. Mondjuk megpróbálhatnánk megérteni a páratlan Goldbach' bizonyítását valahonnan (benne van a Davenport: Multiplicative number theory-ban, illetve azt hiszem, az Iwaniec-Kowalski: Analytic number theory-ban), vagy Pintz Jánosék valamelyik újabb eredményét Goldbach' vagy ikerprím' ügyben (Pintz honlapján ott vannak a cikkei). Ez szerintem elég erős matematika, biztosan sokat lehetne fejlődni valamelyik tétel bizonyítását elolvasva.
|
|
|
| [559] Fernando | 2010-03-14 23:36:38 |
 Üdvözlök mindenkit a Nemzetközi PÍ-napon!
Nos, az utolsó komplex és valós függvénytan előadásunkon mondta az oktató: "Ha bebizonyítod a Riemann-hipotézist, akkor csak valósból kell húzni!" :) Ennek szellemében: aki itt bizonyítja a Goldbach-sejtést, netán talál páratlan tökéletes számot, vagy amúgy mellékeredményként kijön neki a Riemann-hipotézis, annak fizetek egy sört, ha legközelebb Bp-n járok! Egye fene, a Riemann megér két sört is!!
Ma belefér ennyi lazaság...de a szavam állom! :)
|
|





 1)(6m
1)(6m (x)-2. Azért adjuk hozzá az összeghez n-t, mert m valójában nem tagja a sorozatoknak, (azért nem, mert nem szerepel ama táblázatban, ezt sem részletezem).
(x)-2. Azért adjuk hozzá az összeghez n-t, mert m valójában nem tagja a sorozatoknak, (azért nem, mert nem szerepel ama táblázatban, ezt sem részletezem). 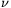 függvény létjogosultságát.
függvény létjogosultságát.  (d) d különböző prímsztóinak a száma. Az eljárást folytatva könnyen belátható, hogy, ha minden a-nál nagyobb prímhez a darab sorozatot rendelünk, akkor a sorozatokból kimaradó egészek száma x-ig
(d) d különböző prímsztóinak a száma. Az eljárást folytatva könnyen belátható, hogy, ha minden a-nál nagyobb prímhez a darab sorozatot rendelünk, akkor a sorozatokból kimaradó egészek száma x-ig  (d)=
(d)= 3nm
3nm x|k
x|k N." Egyrészt ez kézlengetés: olyan, mintha úgy bizonyítanál, hogy hát végtelen sok prím van, elég szabálytalan hézagokkal, úgyhogy az a hézag végtelen sokszor 2. Másrészt, ha az egyenlőtlenségedben tényleg < áll fenn egy idő után mindig, attól még lehet, hogy a két oldal különbsége korlátos. És ekkor nem vagy kész. Mi van, ha a jobb oldal=bal oldal+43, ha x elég nagy?
N." Egyrészt ez kézlengetés: olyan, mintha úgy bizonyítanál, hogy hát végtelen sok prím van, elég szabálytalan hézagokkal, úgyhogy az a hézag végtelen sokszor 2. Másrészt, ha az egyenlőtlenségedben tényleg < áll fenn egy idő után mindig, attól még lehet, hogy a két oldal különbsége korlátos. És ekkor nem vagy kész. Mi van, ha a jobb oldal=bal oldal+43, ha x elég nagy? 
 és mivel
és mivel 