Fórum: A Goldbach-sejtésről

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50]

Szeretnél hozzászólni? Jelentkezz be.

[739] Zsuzsy

2010-07-04 21:08:54

Kedves Zilberbach!

Szerintem okfejtésed nem eléggé alapos. Mint írod: "hiszen azonos nagyságrendű számok összeadásával max. egy nagyságrendet változnak a számok, és azt is csak korlátozottan." Ki köti ki neked, hogy két azonos nagyságrendű prímet kell összeadni?

Abban igazad van, ha 3 nagyságrenden keresztül nem fordul elő prímszám, akkor gondban vagyunk. Szerencsére van egy tétel, ami azt állítja n és 2n között mindig van prím.

[738] Zilberbach

2010-07-04 16:45:52

Kedves Huszár Kristóf!

Még annyit had jegyezzek meg, hogy a matamatika nem csak a pontos számítások birodalma. Természetes az is. De ennél azért sokkal több: a számokról való gondolkodás és elmélkedés tudománya is.

Üdvözlettel: Zilberbach

Előzmény: [737] Zilberbach, 2010-07-04 16:40:50

[737] Zilberbach

2010-07-04 16:40:50

Kedves Huszár Kristóf!

A Goldbach sejtés egy könnyen megérthető állítás, még az olyan kezdetleges matematika tudással rendelkező személyek számára is, mint amilyen én vagyok.

A bizonyítása illetve a cáfolata már jóval nehezebb feladat, nem is sikerült eddig még senkinek.

Be kell ismernem, hogy az ezzel kapcsolatos anyagok egy részét nem értem.

Ebből a hozzáászólásból is egy kis rosszallást érzek ki: Hogy mer egy a matematikában ennyire járatlan személy (ez lennék én) megpróbálkozni azzal, hogy érdemben hozzászól ehhez a témához?

Csak azért tettem, mert úgy gondoltam lehet hogy az én ötletem járul hozzá majd a megoldáshoz. Könnyen lehet, hogy nem így lesz, akkor elnézést kérek mindenkitől akit az ötletem bosszantott. De a személyem alkalmatlanságának bizonygatása helyett inkább a fölvetett ötletről kellene szólni, érdemben.

(Zárójeles kérdésedre a válasz: nem tudom a pontos nagyságrendet sem. Minden esetre még jóval három nagyságrendnyi prímszám-mentes tartomány előtt.)

Előzmény: [736] Huszár Kristóf, 2010-07-04 15:29:18

[736] Huszár Kristóf

2010-07-04 15:29:18

Kedves Zilberbach!

Érdemben nem tudok és nem is szeretnék hozzászólni a témához. Annyit azért tudok, hogy ez egy igen mély és nehéz állítás. Valószínűleg évekig tartó tanulással tudnék eljutni olyan szintre, hogy a sejtéssel kapcsolatos eddigi eredményeket megértsem. Azt gondolom azonban, hogy az alábbiakat érdemes áttanulmányoznia mindenkinek, aki a matematika iránt érdeklődik. Az utolsó link csak a téma miatt került ide.

A matematikai bizonyításokról (angolul)

Laczkovich Miklós: Mi a matematika? Előadás a Mindentudás Egyetemén

A Goldbach-sejtés állítása a 4^.10¹⁸-nál kisebb páros számokra biztosan igaz

(Ezek már elég nagy számok, pontosan hol kezdődne az a nagyságrend, ahol már nem lenne igaz?)

Üdvözlettel: Huszár Kristóf

[735] Zilberbach

2010-07-04 12:54:01

Kedves Tibixe!

Az általad említett példában a négyzetszámok előfordulása ugyan csökkenő tendenciát mutat, a nagyságuk (értékük) azonban meredeken emelkedik, és ez kiegyensúlyozza a helyzetet - ezért a nagy számoknál nincs gond, összerakhatóak két négyzetszám összegeként.

A páros számok - prímszámok viszonylatában azonban nincs ami kiegyenlítse a prímszámok egyre fogyatkozó arányát.

Előzmény: [734] Tibixe, 2010-07-04 12:02:17

[734] Tibixe

2010-07-04 12:02:17

Ugyanezzel a gondolatmenettel még további magasságokba (mélységekbe) is szállhatunk:

1. A 4k+1 alakú prímszámok sűrűsége 1-től x-ig kb.

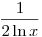
$\frac{1}{2 \ln x}$

Ez elég lassan csökken.

2. A négyzetszámok sűrűsége 1-től x-ig kb.

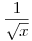
$\frac{1}{\sqrt{x}}$

. Ez viszonylag gyorsan csökken, annyira, hogy a fenti sűrűséghez képest elhanyagolható ( az arányuk tart a nullához ).

Tehát kizárt dolog, hogy minden 4k+1 alakú prímszám kifejezhető legyen két négyzetszám összegeként.

Fermat meg buta, és ez az öt bizonyítás is mind hibás.

Előzmény: [732] Zilberbach, 2010-07-04 07:43:37

[733] Zilberbach

2010-07-04 08:29:58

"hiszen az összeadással max. egy nagyságrendet változnak a számok, és azt is csak korlátozottan."

A szövegrész javítva:

"hiszen azonos nagyságrendű számok összeadásával max. egy nagyságrendet változnak a számok, és azt is csak korlátozottan."

Előzmény: [732] Zilberbach, 2010-07-04 07:43:37

[732] Zilberbach

2010-07-04 07:43:37

Készítsünk statisztikát a természetes számokról: a számegyenesen a nullától a nagy számok irányába haladva - mondjuk egy milliónként.

A következő eredményeket fogjuk kapni:

1. Állandóan, monotonon mindig félmillió páros szám fordul elő, egy milliónként.

2. A prímszámok előfordulási gyakorisága lassan de biztosan, monotonon csökken (egy milliónként). (A prímszámok előfordulási gyakoriságára több jól közelítő képlet is forgalomban van, de mind ezt jósolja,és ezt a statisztikák is alátámasztják).

3. Fönti két állításból együttesen az következik, hogy a páros Goldbach sejtés a nagyon nagy számok tartományában már nem lesz érvényes, mert a relatíve egyre csökkenő mennyiségben előforduló prímszámokból már nem fogunk mindig találni két olyat amiből a változatlan eiőfordulási gyakoriságu (nagy) páros számokat mind összerakhatjuk.

Hogy egyértelműbb legyen:

Ha pl. eljutunk abba a sivár tartományba, ahol mondjuk 3 nagyságrenden keresztül nem fordul elő prímszám, akkor az ebbe a nagyságrendbe eső páros számok nagy részéhez már nem tudunk találni két olyan prímszámot amiből össze tudnánk rakni, hiszen az összeadással max. egy nagyságrendet változnak a számok, és azt is csak korlátozottan.

Jogos a reklamáció, hogy a fönti meggondolások a még nagyobb számok tartományában a páratlan Goldbach sejtésre is érvényesek kellene hogy legyenek - de azt már bizonyították.

Erre csak azt tudom mondani hogy az a bizonyítás bizony igen igen hosszadalmas és bonyolult, lehet hogy nem sokan vették a fáraadtságot, hogy tényleg nagyon alaposan ellenőrizzék.

[731] Maga Péter	2010-06-06 20:40:04
Szenzáció!

[730] bily71

2010-05-30 16:49:13

Hát ez sem jött össze... Mire leírtam köddé foszlott. Arra játszottam, hogy, ha kétféleképp számolom ki h-t és behelyettesítem (3)-at, ami elvileg nem lehet 0, akkor ellentmondásra jutok, ehelyett kaptam egy akkora azonosságot, amekkorát csak lehet, azzal pedig nem sokra megyek.

Ezzel szemben a [718]-as út járhatónak tűnik, csak ne lenne ilyen bonyolult.

Előzmény: [729] bily71, 2010-05-30 13:07:50

[729] bily71

2010-05-30 13:07:50

Most pedig teszünk egy kis kitérőt, pontosabban: megpróbáljuk levágni a kanyart.

Jelölje n az n-edik 6 többszöröst, (n $\in$ N,x $\in$ R) vagyis $n=\left[\frac{x}{6}\right]$ !

Ekkor az n-nél nem nagyobb k $\ne$ 6uv $\pm$ u $\pm$ v alakú k egészek száma n függvényében

$f(n)=n-\left[\frac{n-1}{5}\right]-\left[\frac{n+1}{5}\right]-\left[\frac{n-1}{7}\right]-...,$

(1)

ahol k,u,v $\in$ N.

Ha a $\pi$ ₂^* jelöli a 6k $\pm$ 1 alakú n-nél nem nagyobb ikerprímeket számláló függvényt, akkor

$\pi$ ₂^*(n)=2f(n),

(2)

vagyis $\pi_2^*(n)\approx\sum_{d|P_5}\mu(d)2^{\omega(d)+1}\left[\frac{n}{d}\right]$ .

Tételezzük fel, hogy $\pi$ ₂^* korlátos! Ekkor létezik a legnagyobb ikerprímpár: 6m-1 és 6m+1.

Tételezzük fel, hogy p_r²<m $\le$ p_r+1², ahol p_r az r-edik 6k $\pm$ 1 alakú prím! Ekkor $\pi$ ₂^* definíciójából következik, hogy, ha p_r+1<n $\le$ p_r+2, akkor

$\pi_2^*(p_{r+2}^2)-\pi_2^*(p_{r+1}^2)=-2\left[\frac{n+a_1}{p_{r+2}}\right]-2\left[\frac{n+a_2}{p_{r+2}}\right]+2\left[\frac{n+a_3}{5p_{r+2}}\right]+...=0,$

(3)

ahol a_i=d-b_i, ahol b_i a d differenciájú számtani sorozat első eleme.

Jelölje $\pi$ ^* a 6k $\pm$ 1 alakú prímeket számláló függvényt! Ekkor:

1.Tétel:

$\pi^*(n)=2n-\left[\frac{n-1}{5}\right]-\left[\frac{n+1}{5}\right]-\left[\frac{n-1}{7}\right]-\left[\frac{n+1}{7}\right]+\left[\frac{n+6}{35}\right]+\left[\frac{n+29}{35}\right]-...,$

(4)

vagyis $\pi^*(n)\approx\sum_{d|P_5}\mu(d)2\left[\frac{n}{d}\right]$ .

Bizonyítás: tekintsük az alábbi sorozatokat: 5,11,17,23... és 7,13,19,25...! Az első sorozatban $a=n-\left[\frac{n-1}5\right]-\left[\frac{n+1}7\right]+\left[\frac{n+29}{35}\right]-...$ darab prím van, a második sorozatban $b=n-\left[\frac{n+1}5\right]-\left[\frac{n-1}7\right]+\left[\frac{n+6}{35}\right]-...$ darab, ezek összege kiadja $\pi$ ^*-t, vagyis $\pi$ ^*(n)=a+b.

Vegyük (2) és (4) különbségét, jelölje ezt h, vagyis

h(n)= $\pi$ ^*(n)- $\pi$ ₂^*(n)!

(5)

Ekkor h(n) tulajdonképp azon p=6k $\pm$ 1 prímeket számlálja, amelyekre q=p $\pm$ 2 nem prím.

Mindjárt folytatom.

Előzmény: [722] bily71, 2010-05-23 18:01:15

[722] bily71	2010-05-23 18:01:15
Azt hiszem megvan a c értéke, de mégegyszer leellenőrzöm.
Előzmény: [721] bily71, 2010-05-22 10:55:18

[721] bily71	2010-05-22 10:55:18
Vagyis nem a számlálóban van, de annyi bizonyos, hogy a hiba középértéke negatív.:)
Előzmény: [720] bily71, 2010-05-22 10:52:25

[720] bily71	2010-05-22 10:52:25
Ezen dolgozom:) Úgy néz ki, hogy a számlálóban lévő 1/2 sem mindig annyi, a középérték is d-től függ.
Előzmény: [719] Fálesz Mihály, 2010-05-22 07:42:17

[719] Fálesz Mihály	2010-05-22 07:42:17
Mekkora a c?
Előzmény: [718] bily71, 2010-05-21 21:46:10

[718] bily71

2010-05-21 21:46:10

Ha a d nevezőjű tagokat "összevonjuk", akkor az $A=\left[\frac{x+a_1}{d}\right]+\left[\frac{x+a_2}{d}\right]+...+\left[\frac{x+a_n}{d}\right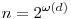]$ összeg, (ahol $n=2^{\omega(d)}$ , a_i=d-b_i, ahol b_i a d differenciájú sorozat kezdőtagja), helyettesíthető az $\left[\frac{2^{\omega(d)}x}{d}-\frac12\right]$ taggal, ugyanis minden x-re igaz, hogy $\left[\frac{2^{\omega(d)}x}{d}-\frac12-c\right]\le{A}\le\left[\frac{2^{\omega(d)}x}{d}-\frac12+c\right]$ , ahol c d-től függő pozitív racionális.

Ezzel a helyettesítéssel párokat képezve zárójelezhetünk az f összegzésben, úgy, hogy a párok egyik tagjának nevezője p₁-szerese legyen a másikénak, azután a párokat helyettesítve újból zárójelezhetünk újabb párokat képezve, úgy, hogy a párok egyik tagjának nevezője p₂-szerese legyen a másikénak, és így tovább. Ezzel elérhetjük, minden lépésnél minden művelet kivonás legyen, így végül bizonyos összefüggések érvényesülése révén mindig olyan párt kapunk, hogy a g(x) $\le$ f(x) reláció teljesül minden x-re, ahol $g(x)=\left[x\prod\left(1-\frac{1}{p/2}\right)\right]$ , ahol p a szitában lévő prímeket jelöli, és mivel g nem korlátos, így f sem lehet az.

Előzmény: [716] Maga Péter, 2010-05-16 10:54:53

[717] bily71

2010-05-16 12:55:01

Nálam ennek a megszámolásnak elvi jelentősége van. Meg tudom mondani pontosan hány x-nél nem nagyobb ikerprímpár van anélkül, hogy rámutatnék egyre is. Vagyis nem kell eldönteni az x-nél nem nagyobb pozitív egészekről, hogy prímek-e. Nem biztos, hogy f-nek van gyakorlati haszna is, lehet, hogy gyorsabb letesztelni minden pozitív egészet, hogy aztán megszámoljuk az olyan prímpárokat, amelyek különbsége 2.

Hogy f korlátos-e, az már más kérdés. A [711]-beli F biztos, hogy nem korlátos, ezt be tudom bizonyítani. Az |f(x)-F(x)| értéke, vagyis a hiba nem lehet akármekkora, ennek meghatározása már nehezebb feladat.

Előzmény: [716] Maga Péter, 2010-05-16 10:54:53

[716] Maga Péter	2010-05-16 10:54:53
,,(...) sikerült megszámolnom a k $\ne$ 6nm $\pm$ n $\pm$ m alakú pozitív egészeket x-ig.'' Ez megint egy egészen elképesztő eufemizmus. Miféle megszámolás az, amelyből még azt sem tudjuk megmondani, hogy az ilyen alakú számok x-ig vett száma korlátos-e, mint x függvénye?
Előzmény: [715] bily71, 2010-05-16 09:21:43

[715] bily71	2010-05-16 09:21:43
Ettől az f-től mindkét függvény, az is amelyikben $2^{\omega(d)}$ az egészrészjelen belül van, az is, amelyikben kívül van jelentősen eltér, ezért egyelőre feladom. Most megelégszem azzal, hogy végre sikerült megszámolnom a k $\ne$ 6nm $\pm$ n $\pm$ m alakú pozitív egészeket x-ig.
Előzmény: [712] bily71, 2010-05-16 08:18:09

[714] Róbert Gida

2010-05-16 09:12:29

Sokat nem szitáltál életedben, de hogy valami értelem is legyen a topikban: az alábbi f valóban az n-nél nem nagyobb ikerprímpárok számát adja meg (p,p+2=q $\le$ n), logikai szitával, bár nyilván ezzel hosszú ideig tart kiszámolni:(mindenesetre n=9..1000-ig helyes eredményt ad.). Pari-Gp-ben felírva, hogy könnyen ellenőrizhető legyen:

f(n)=s=0;for(i=2,n*n,mul=moebius(i)*(factor(i)[omega(i),1]<=sqrtint(n));if(mul!=0, s+=mul*sumdiv(i/(2-i%2),d,pt(n,(2-i%2)*d,i))));return(s+n-1+pi2(sqrtint(n)+2))

pi2(n)=sum(i=1,n-2,isprime(i)&&isprime(i+2))

pt(n,d,i)=e=lift(Mod(2*d/i,d))*i/d;return((n-e)\i+1-(e<=2))

Előzmény: [711] bily71, 2010-05-15 21:13:49

[713] bily71	2010-05-16 09:01:11
Pontosabban b a d differenciájú sorozat kezdőtagja.
Előzmény: [712] bily71, 2010-05-16 08:18:09

[712] bily71

2010-05-16 08:18:09

Megvan hol hibáztam!

Nem mindegy, hogy a d differenciájú sorozat kezdőtagja kisebb, vagy nagyobb-e mint d. A pontos darabszámot ezzel a taggal kapjuk meg: $\left[\frac{\left[\frac{x}{6}\right]+a}{d}\right]=\left[\frac{x+6a}{6d}\right]$ , ahol a=d-b, ahol b=6m $\pm$ 1 $\pm$ m.

5²<x $\le$ 7² esetén

$f(x)=\left[\frac{x}{6}\right]-\left[\frac{x-6}{30}\right]-\left[\frac{x+6}{30}\right]-\left[\frac{x-6}{42}\right]-\left[\frac{x+6}{42}\right]+\left[\frac{x-6}{210}\right]+\left[\frac{x+6}{210}\right]+\left[\frac{x+36}{210}\right]+\left[\frac{x+174}{210}\right]$

Így már a tényleges darabszámot kapjuk.

Előzmény: [711] bily71, 2010-05-15 21:13:49

[711] bily71

2010-05-15 21:13:49

Beszélgessünk még egy kicsit az ikerprímekről.

A pontos darabszámot a következő képlet adja meg:

0 $\le$ x $\le$ 5² esetén

$f(x)=\left[\frac{x}{6}\right]-\left[\frac{x-6}{30}\right]-\left[\frac{x+6}{30}\right]$

5²<x $\le$ 7² esetén

és így tovább.

Ebben a formában hajszál pontosan meg kellene, hogy kapjuk azon x-nél nem nagyobb pozitív egészek számát, amelyek nem 6nm $\pm$ n $\pm$ m alakúak, mégsem ez történik. Miért?? Úgy néz ki, hogy itt is kell a korrigálni, egy n-1 taggal. Tehát a fenti tulajdonságú egészek száma f+(n-1).

f-et a "GraphCalc" nevű programmal vizsgálgattam. (Megbízható ez a program?) Azt tapasztaltam, hogy a [689]-es képlet mégsem jó közelítés. Jobb közelítést kapunk az eredtei elképzelésem szerint, a 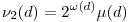$\nu_2(d)=2^{\omega(d)}\mu(d)$ taggal, vagyis a következő képlettel:

$F(x)=\sum_{d|P_5}\nu_2(d)\left[\frac{x}{6d}\right]$

A két függvény f és F elképesztően "simul" egymáshoz, a hiba, legalábbis, ameddig vizsgáltam, nem nagyobb, mint n, vagyis, mint a szitában lévő prímek száma.

Előzmény: [705] Fálesz Mihály, 2010-05-12 18:34:31

[710] bily71	2010-05-14 21:30:50
"Ha egy kiváló idős tudós valamiről azt állítja, hogy lehetséges, majdnem biztosan igaza van, de ha azt mondja, hogy lehetetlen, akkor valószínüleg téved." (Arthur C. Clarke)

[709] bily71	2010-05-12 22:21:51
Javítás: "A darabszám hibája egyébként attól függ..."
Előzmény: [707] bily71, 2010-05-12 22:17:04

Már regisztráltál?
Új vendég vagy?