| [35] Kós Géza | 2003-11-29 22:30:45 |
 Szia Péter,
Bocs` a hosszú csendért...
A megoldásod jó, a következő napokban megpróbálom még egyszer összefoglalni, és ábrákat rajzolni hozzá.
A legfontosabb hiányzó információ az eredmény numerikus közelítése. A megoldásból kiolvasható, hogy a  szög és a p0 szám a szög és a p0 szám a
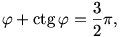
illetve
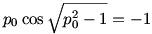
egyenlet megoldása, közelítőleg
  12,55o, p0 12,55o, p0 4,6033. 4,6033.
|
| Előzmény: [34] Pach Péter Pál, 2003-11-26 22:36:49 |
|
| [34] Pach Péter Pál | 2003-11-26 22:36:49 |
 A Viasat 3-on és a Sat 1-en, mindkettőn a Stuttgart-Glasgow Rangers. Egyébként a Stuttgart nyert 1:0-ra Wenzel góljával. A Viasat 3-on még lesz egy részletes összefoglaló az Ajax-Milan meccsről.
Térjünk vissza a feladathoz! Folytassuk Jerry stratégiájával! (Most p<p0.) Jerry stratégiája azért lesz kicsit bonyolultabb, mert mindenre fel kell készülnie, arra is, hogy Tom nem indul el rögtön, amint ő elhagyja k-t, arra is, hogy esetleg többször irányt változtat, …
Legyen  olyan kicsi, hogy még olyan kicsi, hogy még 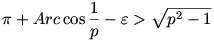 is teljesüljön. Először is Jerry elhelyezkedik a k kör Tommal átellenes pontjában. Ha Jerry k érintőjén futna ki, (Tom pedig a hosszabb utat választaná,) akkor az elején még pihenhetne addig, amíg TKJ is teljesüljön. Először is Jerry elhelyezkedik a k kör Tommal átellenes pontjában. Ha Jerry k érintőjén futna ki, (Tom pedig a hosszabb utat választaná,) akkor az elején még pihenhetne addig, amíg TKJ = = - - nem lesz. Ezért amíg TKJ nem lesz. Ezért amíg TKJ   - - , addig Jerry egyszerűen elindul a KJ sugáron kifelé. Amint TKJ , addig Jerry egyszerűen elindul a KJ sugáron kifelé. Amint TKJ   - - lesz, Jerry a k körhöz húzott érintőn folytatja útját, szintén kifelé. (Azon, amelyik a partot Tom pillanatnyi helyzetétől távolabbi pontban metszi.) Könnyen végiggondolhatjuk, hogy Tom irányváltoztatásai Jerry számára még kedvezőbbé teszik a helyzetet. Az is igaz, hogyha Jerry ezt a stratégiát követi, akkor korlátos időn belül kiér a partra. (K-tól minden pillanatban maximális sebességének legalább cos lesz, Jerry a k körhöz húzott érintőn folytatja útját, szintén kifelé. (Azon, amelyik a partot Tom pillanatnyi helyzetétől távolabbi pontban metszi.) Könnyen végiggondolhatjuk, hogy Tom irányváltoztatásai Jerry számára még kedvezőbbé teszik a helyzetet. Az is igaz, hogyha Jerry ezt a stratégiát követi, akkor korlátos időn belül kiér a partra. (K-tól minden pillanatban maximális sebességének legalább cos  -szeresével távolodik, ahol -szeresével távolodik, ahol  az a bizonyos ideális szög. Vagyis az a bizonyos ideális szög. Vagyis 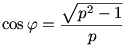 .) Ezért p0 definíciója miatt Jerry biztonságban kiér a partra. .) Ezért p0 definíciója miatt Jerry biztonságban kiér a partra.
Ezzel megoldottuk a klasszikus feladatot.
|
| Előzmény: [33] Rácz Béla, 2003-11-26 21:03:48 |
|
| [33] Rácz Béla | 2003-11-26 21:03:48 |
 Le vagyok nyűgözve.
Peti, melyik adón megy meccs?
Géza, ne búsulj: lehet, hogy nem vagyok aktív résztvevője a Tom és Jerrynek, de legalább elvégeztem a TeX gyorstalpalót! És nagy érdeklődéssel olvasom a megoldásokat!
|
|
| [32] Pach Péter Pál | 2003-11-26 20:48:55 |
 Képzeljük azt, hogy Tom valamilyen okból, (pl. mert már megoldotta a feladatot és nem akarja Jerryt irányváltoztatásra kényszeríteni) a hosszabbik úton indul el ahhoz a ponthoz, ahol Jerry várhatóan partot fog érni. Tomnak eddig a pontig 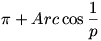 , Jerrynek pedig , Jerrynek pedig 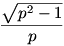 utat kell megtennie. Azt állítjuk, hogy az általunk keresett kritikus p0 érték esetén éppen egyszerre érkeznek oda: utat kell megtennie. Azt állítjuk, hogy az általunk keresett kritikus p0 érték esetén éppen egyszerre érkeznek oda:
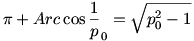
Végiggondolhatjuk, hogyha p ennél nagyobb, akkor Tom ér előbb oda, ha pedig p ennél kisebb, akkor Jerry. Egyébként p0 4,603. Két dolgot kell bizonyítani, azt hogy p<p0 esetén Jerry ki tud jutni a partra, illetve azt, hogy p 4,603. Két dolgot kell bizonyítani, azt hogy p<p0 esetén Jerry ki tud jutni a partra, illetve azt, hogy p p0 esetén Tom ezt meg tudja akadályozni. p0 esetén Tom ezt meg tudja akadályozni.
Kezdjük az utóbbival!
Jerry és Tom távolságát jellemezzük JKT -gel. -gel.
Tom stratégiája eléggé egyszerű: abban a pillanatban, hogy Jerry eléri a K körüli p-1 sugarú k kört, elindul felé olyan irányban, hogy TKJ csökkenjen. Amikor Jerry már a k körön kívül van, kisebb a szögsebessége, így TKJ csökkenjen. Amikor Jerry már a k körön kívül van, kisebb a szögsebessége, így TKJ csökken. Amennyiben TKJ csökken. Amennyiben TKJ nullává válik, Tom fenntartja ezt a helyzetet, egészen addig, amíg Jerry partot ér. (Ezt meg tudja tenni, hiszen nagyobb a szögsebessége.) Ha Jerry közben visszatér k-ba, Tom megáll és vár, hiszen úgysem tud mit tenni. De Jerrynek előbb-utóbb meg kell próbálkozni egy végső kiúszással. A továbbiakban onnantól figyeljük a történteket, ahonnan Jerry már nem tér vissza k belsejébe. Azt állítjuk, hogy a partnak minden egyes pontjához előbb ér oda Tom, mint Jerry. (Esetleg éppen egyszerre vele.) Először azt az esetet nézzük meg, amikor a part egy olyan pontját szemeli ki magának, amivel olyan egyenes szakasz köti össze, ami nem metsze bele k-ba. Az előző feladatban beláttuk, hogy Jerry számára az az ideális, amikor kérintője mentén úszik ki. De p0 definíciója következtében még ilyenkor sem ér ki előbb, mint Tom. (A többi esetben Tom még előbb lenullázza TKJ nullává válik, Tom fenntartja ezt a helyzetet, egészen addig, amíg Jerry partot ér. (Ezt meg tudja tenni, hiszen nagyobb a szögsebessége.) Ha Jerry közben visszatér k-ba, Tom megáll és vár, hiszen úgysem tud mit tenni. De Jerrynek előbb-utóbb meg kell próbálkozni egy végső kiúszással. A továbbiakban onnantól figyeljük a történteket, ahonnan Jerry már nem tér vissza k belsejébe. Azt állítjuk, hogy a partnak minden egyes pontjához előbb ér oda Tom, mint Jerry. (Esetleg éppen egyszerre vele.) Először azt az esetet nézzük meg, amikor a part egy olyan pontját szemeli ki magának, amivel olyan egyenes szakasz köti össze, ami nem metsze bele k-ba. Az előző feladatban beláttuk, hogy Jerry számára az az ideális, amikor kérintője mentén úszik ki. De p0 definíciója következtében még ilyenkor sem ér ki előbb, mint Tom. (A többi esetben Tom még előbb lenullázza TKJ -et.) -et.)
Az is lehet, hogy Jerry egy kicsit „köröz”, esetleg csigavonalszerűen úszik ki a partra. Ilyenkor a Jerry számára minimális úthosszt úgy kapjuk, hogy egy ívet k-n fut (esetleg többször is körbefut k körvonalán), utána pedig érintőirányban kiúszik a partra. De Tom és Jerry szögsebessége megegyezik, így együtt „köröznek”, utána pedig már az előbb elmondottak érvényesek.
Elkezdődött a focimeccs a TV-ben, úgyhogy a másik részt csak később írom le. (Esetleg a szünetben…)
|
| Előzmény: [31] Kós Géza, 2003-11-24 19:09:43 |
|
| [31] Kós Géza | 2003-11-24 19:09:43 |
 Jöjjön a klasszikus feladat megoldása.
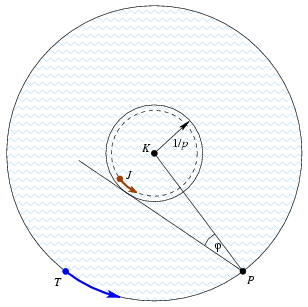
A 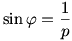 eredménynek van egy nagyon fontos geometriai jelentése. Az ilyen irányú egyenes érinti a K körüli, 1/p sugarú kört. Ez a kör pedig arról nevezetes, hogy a kerületén Jerry éppen olyan szögsebességgel tud úszni, mint amilyennel Tom a parton fut. eredménynek van egy nagyon fontos geometriai jelentése. Az ilyen irányú egyenes érinti a K körüli, 1/p sugarú kört. Ez a kör pedig arról nevezetes, hogy a kerületén Jerry éppen olyan szögsebességgel tud úszni, mint amilyennel Tom a parton fut.
Tételezzük fel, hogy Jerry egy 1/p-nél kisebb sugarú körön úszik körbe. Ezen a körön Jerry szögsebessége mindig nagyobb, mint Tom szögsebessége, Jerry ezért elérheti, hogy éppen Tommal ellentétes oldalon legyen. Mindezt persze Tom is nagyon jól tudja. Tom tehát egy helyben áll, és csak akkor mozdul meg, ha 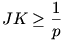 ... ...
Mi történik ezután?
|
 |
|
|
|
| [28] Kós Géza | 2003-11-24 11:07:50 |
 A számolás egyszerűbben is megy, ha tudjuk, hogy a sin  a kérdés. a kérdés.
Legyen a kör sugara 1, Jerry sebessége 1, Tom sebessége p. Azt az  szöget kell megtalálnunk, amire szöget kell megtalálnunk, amire 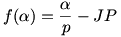 minimális. minimális.
A koszinusz-tételből
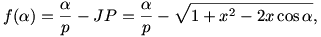
és, a szinusz-tételt is felhasználva,
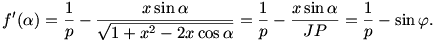
A korábbi képletekből látszik jobban, hogy csak 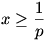 esetén kapunk értelmes eredményt. esetén kapunk értelmes eredményt.
|
 |
| Előzmény: [26] Pach Péter Pál, 2003-11-23 23:15:41 |
|
|
|
| [25] Pach Péter Pál | 2003-11-23 18:55:25 |
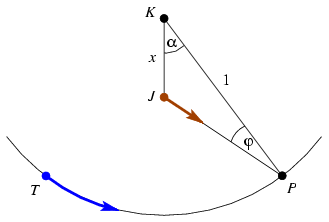
 A kört vegyük egységsugarúnak! A [20]-[22]-[23] hozzászólások jelöléseit fogjuk használni. Képzeljük azt, hogy Tom kezdetben abban a pontban van, ahol a KJ félegyenes metszi a kört. (Az időkülönbséget konstanssal toltuk el.) Tomnak  , Jerrynek pedig , Jerrynek pedig 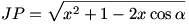 távol távolságot kell megtennie P-ig. (KJP háromszögben JP-re koszinusztételt írtunk fel.) Így távol távolságot kell megtennie P-ig. (KJP háromszögben JP-re koszinusztételt írtunk fel.) Így 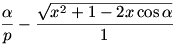 kifejezést akarjuk maximalizálni. A függvény p-szeresének (konstansszorosának) deriváltja kifejezést akarjuk maximalizálni. A függvény p-szeresének (konstansszorosának) deriváltja 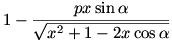 . A . A 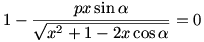 egyenletet megoldva: egyenletet megoldva:
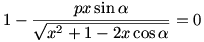
x2+1-2xcos  =p2x2sin2 =p2x2sin2 =p2x2-p2x2cos2 =p2x2-p2x2cos2
A cos  -ban másodfokú egyenlet általunk keresett megoldása az egyszerűsítések után a [22]-ben már említett: -ban másodfokú egyenlet általunk keresett megoldása az egyszerűsítések után a [22]-ben már említett:
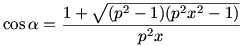
KJP háromszögben felírt szinusztételből: 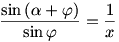 , amiből , amiből 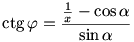 . .
Először számoljuk ki sin  -t: -t:
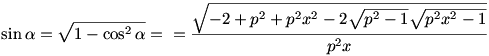
Bevezetve a 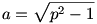 és a és a 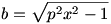 egyszerűsítő jelöléseket, kiszámoljuk ctg egyszerűsítő jelöléseket, kiszámoljuk ctg  -t: -t:
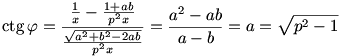
Tehát a Jerry számára ideális  szög Arcctg (p2-1). szög Arcctg (p2-1).
Előfordulhat, hogy az így kapott  szög olyan nagy, hogy ilyen szög alatt a körvonal egyik pontjából sem látjuk KJ-t. Határozzuk meg azt a legkisebb x távolságot, amihez a körvonalnak már van olyan pontja, amelyből KJ szög olyan nagy, hogy ilyen szög alatt a körvonal egyik pontjából sem látjuk KJ-t. Határozzuk meg azt a legkisebb x távolságot, amihez a körvonalnak már van olyan pontja, amelyből KJ  szög alatt látszik! Ilyenkor a szög alatt látszik! Ilyenkor a  szögű látókör éppen érinti a kört. KJP háromszögben felírt szinusztételből: szögű látókör éppen érinti a kört. KJP háromszögben felírt szinusztételből: 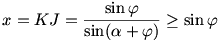 , az egyenlőség meg is valósulhat. , az egyenlőség meg is valósulhat.
Tehát azt kaptuk, hogy amennyiben Jerry távolsága a parttól legfeljebb 1-sin  , az ideális , az ideális  szögre szögre 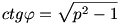 . Bocs mindenkitől, hogy ilyen hosszan írtam. . Bocs mindenkitől, hogy ilyen hosszan írtam.
|
|
| [24] Kós Géza | 2003-11-22 21:34:43 |
 Szia Péter,
Az eredményt érdemes átírni  -re, úgy sokkal szebb a végeredmény, és a folytatásban is hasznos lesz. -re, úgy sokkal szebb a végeredmény, és a folytatásban is hasznos lesz.
Az is kiderül belőle, hogy Jerrynek mennyire kell ,,közel'' lennie a parthoz. Ha ugyanis a KJ távolság egy bizonyos értéknél kisebb, a képlet nem ad értelmes eredményt.
|
| Előzmény: [22] Pach Péter Pál, 2003-11-21 22:16:16 |
|
|
| [22] Pach Péter Pál | 2003-11-21 22:16:16 |
 Kedves Géza!
A legújabb feladat is kijön deriválással, azonban van egy-két kérdésem. Mit jelent az, hogy Jerry a parthoz közel úszkál? Adott p esetén azt mondjuk, hogy megállapításaink 1- <OJ esetén érvényesek? Gondolom 1<p ki van kötve. Jerrynek milyen irányban szabad úsznia? (Pl. feltehető, hogy P a jobboldali félkörön van?) Ezeken kívül az is problémám, hogy én JKP <OJ esetén érvényesek? Gondolom 1<p ki van kötve. Jerrynek milyen irányban szabad úsznia? (Pl. feltehető, hogy P a jobboldali félkörön van?) Ezeken kívül az is problémám, hogy én JKP -et tudtam jól kezelni, nem pedig -et tudtam jól kezelni, nem pedig  -t. Persze átírhatom -t. Persze átírhatom  -re a végén, de úgy elég ronda lesz (legalábbis szerintem). Arra lennék kíváncsi, hogy van-e valami fontossága a -re a végén, de úgy elég ronda lesz (legalábbis szerintem). Arra lennék kíváncsi, hogy van-e valami fontossága a  szögnek, vagy át lehet térni szögnek, vagy át lehet térni  =JKP =JKP -re. -re.
Egyébként azt kaptam, hogy a (szerintem érdekes) eseteknél 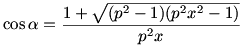 esetén maximális a Jerry javára eltelt idő. esetén maximális a Jerry javára eltelt idő.
Remélem nem számoltam el.
|
|
|
| [20] Kós Géza | 2003-11-20 16:15:30 |
 Most egy kicsit térjünk vissza a klasszikus feladathoz.
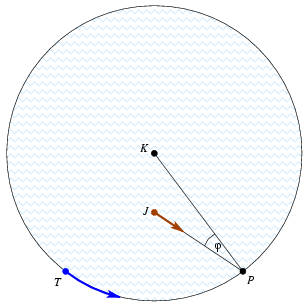
Jerry most kör alakú medencében úszik, közel a parthoz. Látja, hogy Tom az ábra szerinti irányból érkezik. Jerry ismét kiválaszt egy P pontot a parton, és egyenesen oda úszik. A JP szakasz a P-ből húzott sugárral  szöget zár be. Tom most is p-szer gyorsabban fut, mint ahogy Jerry úszik, és nem csak az számít, hogy ki ér oda előbb, hanem az eltelt idők különbsége is. szöget zár be. Tom most is p-szer gyorsabban fut, mint ahogy Jerry úszik, és nem csak az számít, hogy ki ér oda előbb, hanem az eltelt idők különbsége is.
Milyen  szöget válasszon Jerry? szöget válasszon Jerry?
|
 |
|
| [19] Kós Géza | 2003-11-20 16:06:14 |
 Ügyes.
Egy apróság. Az első részben Jerry a sebességtől függetlenül utolérheti az átlót, mert az átló csak véges hosszú utat tehet meg.
|
|
| [18] Pach Péter Pál | 2003-11-19 22:19:18 |
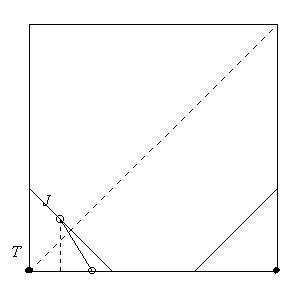
 Folytassuk Tom stratégiájával. (Most 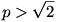 .) Tom az egyik sarokban helyezkedik el. Jerry közelségét veszélyesnek értékeli, amint az a kiválasztott csúcshoz illesztett d befogójú egyenlőszárú derékszögű háromszögbe lép. Megnézi, hogy Jerry az átló melyik oldalán tette ezt, és átszalad (maximális sebességével) a szomszédos csúcsok közül abba, amelyik Jerrytől távolabb van. .) Tom az egyik sarokban helyezkedik el. Jerry közelségét veszélyesnek értékeli, amint az a kiválasztott csúcshoz illesztett d befogójú egyenlőszárú derékszögű háromszögbe lép. Megnézi, hogy Jerry az átló melyik oldalán tette ezt, és átszalad (maximális sebességével) a szomszédos csúcsok közül abba, amelyik Jerrytől távolabb van.
Nem mondtuk még meg, hogy mi alapján határozzuk meg d-t. Természetesen d-t úgy választjuk meg, hogy kezdetben Jerry távolsága ne legyen veszélyes: d<d1. Szeretnénk, hogy mialatt Tom átfut a másik csúcsba, Jerry ne érhesse el a másik csúcshoz tartozó veszélyes körzetet. Hogy Jerry elérje a másik egyenlőszárú, derékszögű háromszöget, legalább 1-2d távolságot kell úszva megtennie, Tom pedig 1 egységnyit fut a parton. (A négyzetet egységoldalúnak vettük.) Mivel Tom sebessége legalább 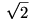 -szöröse Jerryének, ezért d-t elég kicsinek választva elérjük, hogy Jerry biztonságos távolságban maradjon Tomhoz képest. (Legyen -szöröse Jerryének, ezért d-t elég kicsinek választva elérjük, hogy Jerry biztonságos távolságban maradjon Tomhoz képest. (Legyen 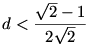 .) .)
Már csak azt kell megvizsgálni, hogy Jerry el tudja-e kapni Tomot az átfutás közben. Ha Jerry az 1. feladat szerinti ideális  szöggel odaúszik a parthoz, de Tomnak már csak hűlt helyét találja, akkor nincs esélye elkapnia Tomot. (A partnak nincs olyan pontja, amit előbb, vagy éppen akkor tudna elérni, mint Tom.) Jerry útjának legyen x a hossza. Ekkor Tomnak legfeljebb x(cos szöggel odaúszik a parthoz, de Tomnak már csak hűlt helyét találja, akkor nincs esélye elkapnia Tomot. (A partnak nincs olyan pontja, amit előbb, vagy éppen akkor tudna elérni, mint Tom.) Jerry útjának legyen x a hossza. Ekkor Tomnak legfeljebb x(cos  +sin +sin ) utat kell megtennie. Tudjuk, hogy ) utat kell megtennie. Tudjuk, hogy 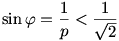 , amiből , amiből  <45o. Ha <45o. Ha 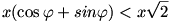 teljesül, akkor Jerry nem kaphatja el Tomot. De: teljesül, akkor Jerry nem kaphatja el Tomot. De:
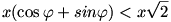
sin 2 <1 <1
Ez azonban tényleg teljesül  <45o miatt. Azt kaptuk, hogy <45o miatt. Azt kaptuk, hogy 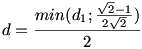 esetén Tom meg tudja valósítani ezt a szaladgálós játékot, és így Jerry nem tudja elkapni. esetén Tom meg tudja valósítani ezt a szaladgálós játékot, és így Jerry nem tudja elkapni.
|
 |
|
| [17] Pach Péter Pál | 2003-11-19 21:59:18 |
 Kicsit fogalmazzuk át a feladatot. Jerry tulajdonképpen Tom tükörképét akarja elkapni, ami a partvonalon mozog maximálisan p sebességgel. A rövidség kedvéért képzeljük azt, hogy szerepcsere történt, és Jerry Tomot el akarja kapni. (Tom tükörképe ugyanúgy viselkedik, mint Tom.)
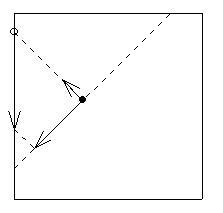
Kezdjük Jerry stratégiájával. (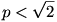 ) Jerry odaúszik az egyik átlóra, és eléri, hogy az átlóra vett vetülete Tom vetületével egybeessen. Ezt nyilván meg tudja tenni, hiszen nagyobb az „átló irányú” sebessége, mint Tomé. A negyedsíkos feladathoz hasonlóan ezt az állapotot fenn tudja tartani, sőt még nincs kihasználva a maximális sebessége. Jerry sebességét vegyük egységnyinek. Legyen ) Jerry odaúszik az egyik átlóra, és eléri, hogy az átlóra vett vetülete Tom vetületével egybeessen. Ezt nyilván meg tudja tenni, hiszen nagyobb az „átló irányú” sebessége, mint Tomé. A negyedsíkos feladathoz hasonlóan ezt az állapotot fenn tudja tartani, sőt még nincs kihasználva a maximális sebessége. Jerry sebességét vegyük egységnyinek. Legyen 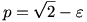 . Jerry a következőket teszi: fenntartja azt az állapotot, hogy vetületeik egybeesnek (ehhez legfeljebb . Jerry a következőket teszi: fenntartja azt az állapotot, hogy vetületeik egybeesnek (ehhez legfeljebb 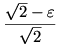 nagyságú sebességkomponens kell, de közben felvesz egy, az átlóra merőleges nagyságú sebességkomponens kell, de közben felvesz egy, az átlóra merőleges  nagyságú sebességkomponenst is, mellyel a négyzet azon feléhez közelít, melybe Tom esik. Ellenőrizhetjük, hogy Jerry eredő sebessége kisebb, mint 1: nagyságú sebességkomponenst is, mellyel a négyzet azon feléhez közelít, melybe Tom esik. Ellenőrizhetjük, hogy Jerry eredő sebessége kisebb, mint 1:
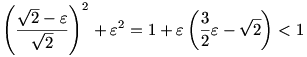
(Ez akkor igaz, ha  nem túl nagy, pontosabban, ha nem túl nagy, pontosabban, ha 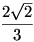 -nál kisebb. Ha ez nem teljesül, akkor Jerry „úgy tesz”, mintha lassabb lenne: maximális sebességét tudatosan a kritikus határ alá csökkenti.) Ha Jerry ezt a stratégiát követi, akkor korlátos időn belül eléri a partot - s ebben a pillanatban elkapja Tomot. -nál kisebb. Ha ez nem teljesül, akkor Jerry „úgy tesz”, mintha lassabb lenne: maximális sebességét tudatosan a kritikus határ alá csökkenti.) Ha Jerry ezt a stratégiát követi, akkor korlátos időn belül eléri a partot - s ebben a pillanatban elkapja Tomot.
|
 |
|
|
| [15] Kós Géza | 2003-11-13 12:20:18 |
 Ügyesen megoldottátok az első két feladatot, jöjjön hát a harmadik. Ez egy incselkedős feladat lesz.
Jerry négyzet alakú tóban úszik, méghozzá nagyon gyorsan, ha nem is olyan nagy sebességgel, mint ahogy Tom fut a parton. Jerry -- szokásához híven -- incselkedik. Úgy akar kiúszni a partra, hogy Tom éppen a vízpart ellentétes pontján legyen. (Ezután kiölti Tomra a nyelvét, de ez most nem lényeges.)
A feladat ismét egy p0 szám megtalálása. Ha p<p0, akkor -- Tom tetszőleges kiinduló pontja és taktikázása esetén is -- Jerry terve sikerülhet. Ha viszont p>p0, akkor Tom mindig tud úgy mozogni, hogy Jerry ne a vele ellentétes ponton másszon ki a partra.
|
|
|
|
|
| [11] Pach Péter Pál | 2003-11-13 00:26:03 |
 Azt fogjuk bizonyítani, hogy 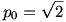 . .
Kezdjük a b) állítás igazolásával! Tom nyerő stratégiája az, hogy mindig a part azon T pontjában tartózkodik, amely illeszkedik a J ponton (a J pont Jerry aktuális tartózkodási helye) keresztül a partvonalat alkotó derékszög (belső) szögfelezőjével párhuzamosan húzott egyenesre. Ha ezt garantálni tudja, akkor Jerry számára nincs menekvés, ugyanis a part egy J pontjához tartozó T-re T=J, ami azt jelenti, hogy abban a pillanatban, hogy Jerry kilép a partra, már Tom is ott van, és elkapja.
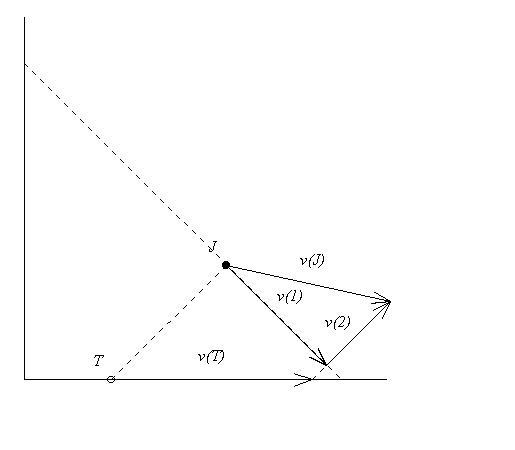
Tom a kiindulási helyzetét meg tudja választani megfelelően (hiszen Jerry nem veszi észre, amikor odaoson), csak azt kell megvizsgálni, hogy fenn tudja-e tartani ezt az állapotot. Jerry sebessége egy vizsgált pillanatban legyen vJ! vJ vektort bontsuk fel egy, a szögfelezőre merőleges v1, és egy azzal párhuzamos v2 nagyságú komponensre. Nyilvánvaló, hogy ha Tom meg akarja őrizni azt a tulajdonságot, hogy JT párhuzamos a szögfelezővel, akkor ebben a pillanatban sebességét 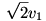 -nek megválasztania, éspedig úgy, hogy a szögfelezőre merőleges egyenesen vett vetülete ugyanarra haladjon, mint Jerryé. (Ez akkor is igaz, ha közben „fordul” a negyedsík csúcspontjában. :-)) -nek megválasztania, éspedig úgy, hogy a szögfelezőre merőleges egyenesen vett vetülete ugyanarra haladjon, mint Jerryé. (Ez akkor is igaz, ha közben „fordul” a negyedsík csúcspontjában. :-))
Szerencsére
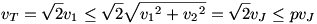
triviálisan teljesül 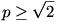 miatt. miatt.
Ezzel a b) részt igazoltuk.
Az eddigiek alapján látszik, hogy Jerrynek érdemes mindvégig a szögfelezőre merőlegesen haladnia, és hogy a következő stratégiával biztosan kijut a partra:
Megfigyeli, hogy attól a T0 ponttól, amelyre JT0 párhuzamos a szögfelezővel, milyen irányban helyezkedik el Tom. Ezután a Tom helyzetével ellentétes irányban a szögfelezőre merőlegesen egyenesen kiúszik a partra. Amennyiben Tom éppen T0-ban, Jerry véletlenszerűen választ a két irány közül. (Pl. ha nem a szögfelezőn van, akkor azt, amelyiknél kevesebbet kell úsznia.) Tomnak legalább 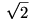 -ször akkora utat kell megtennie, mint Jerrynek, ha el akarja kapni, így -ször akkora utat kell megtennie, mint Jerrynek, ha el akarja kapni, így 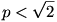 miatt Jerry valóban előbb éri el a part kiszemelt pontját. miatt Jerry valóban előbb éri el a part kiszemelt pontját.
Ezzel bizonyítottuk, hogy a keresett p0 érték a 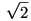 . .
Felteszek három ábrát a megoldáshoz, hogy áttekinthetőbb legyen.
|
 |
|
