Fórum: Matek OKTV

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32]

Szeretnél hozzászólni? Jelentkezz be.

[103] Maga Péter	2004-10-29 20:47:31
Kedves BrickTop! Nem értek veled egyet! A te megoldásodban az általad produktumként említett i! a szummán belül szerepel, tehát ha úgy tekintjük, hogy a szumma és a produktum nem jelentenek zárt alakot, akkor nálad a szummán belüli alak sem zárt, ami minőségében eltér attól a megoldástól, amit LoryBetty írt. Másrészről pedig ez egy verseny, ahol bizonyos szinten együtt kell élned a kitűző gondolkodásával. Ehhez hozzátartozik az, hogy felmérd a feladat nehézségét. Jelen esetben ez azt jelenti, hogy mivel OKTV-ről van szó, várhatóan nem a triviális összegalakot kell szummával felírni. Ha az a kérdés, hogy mennyi 1+2+...+n, arra nem 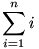$\sum_{i=1}^ni$ a válasz. De azt hiszem, ha a többi példád jól megvan, akkor nem kell aggódnod!
Előzmény: [102] BrickTop, 2004-10-29 13:40:35

[102] BrickTop

2004-10-29 13:40:35

Ha korrekten oldja meg az ember, akkor a szummáshoz is kell egy teljes indukció, csak nevetségesen könnyű. De azt nem várhatják el, hogy csak azért nehezebb úton oldjam meg a feladatot, mert az OKTV-n elvileg nehéz példák vannak.

Szerintem sem korrekt a feladat szövegezése. És a faktoriális hasonló a szummához, mert a produktum egy speciális esete: 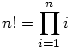$n!=\prod_{i=1}^ni$ , a produktum meg kb. ugyanaz mint a szumma, csak szorzással.

Értem én, hogy a zártabb megoldás sokkal szebb és valószínűleg azt várták el, de ne nekem legyen bajom a pongyola megfogalmazásból.

Előzmény: [100] lorybetti, 2004-10-29 07:18:43

[101] Maga Péter	2004-10-29 09:06:54
Kösz a javítást, azt hiszem, ez a végeredmény jó (BrickTopé is ugyanez, de az biztosan nem zárt)! Egyébként az a₀=0-tól csak egy +2-es eltolással tér el. Azt hiszem, ezt az alakot várták, nem hiszem, hogy létezne "zártabb" alak. Majd szóljatok, ha a 3. feladaton már nem akartok gondolkodni, írok róla! Illetve a többiről is, ha eszembe jut valami érdekes addig.
Előzmény: [97] lorybetti, 2004-10-28 22:09:21

[100] lorybetti

2004-10-29 07:18:43

Hát igen... óvatos versenyző mindkét formulát megadja!

egyébként nem hiszem, hogy csak azt várták el, hogy ilyen "szummás alakra" hozzuk. Ahhoz, hogy az általam leírt képlethez eljusssunk, kellett egy teljes indulció is. Szerintem a feladat kitalálói ezt is elvárják a megoldásban.

[99] Edgar

2004-10-29 00:03:59

Nem lehet, hogy a két képlet ugyanazt takarja?

Jah egyébként nem annyira örülök ennek a feladatnak... nyilvánvaló, hogy zárt alakot várnak el, de ez nem derül ki a feladat szövegéből. Ráadásul a faktoriálist tartalmazó kifejezés *nem* tekinthető egyértelműen zárt alaknak, tehát ezt mindenképpen tisztázni kellett volna!

Előzmény: [97] lorybetti, 2004-10-28 22:09:21

[98] BrickTop	2004-10-28 22:16:16
Ajjaj.... a kifejezés magában foglalja azt is hogy zárt alakban (szummázás nélkül) kell megadni?
Előzmény: [97] lorybetti, 2004-10-28 22:09:21

[97] lorybetti

2004-10-28 22:09:21

Péter, köszönöm!!!!

annyira siettem, hogy efelejtettem leellenőrizni, amit írtam.Helyesen: a₀=2 !!!

Mindenkitől elnézést kérek! Egyébként szerintem nem ez a végeredmény.

Hanem: a_n=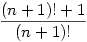 $\frac{(n+1)!+1}{(n+1)!}$

Előzmény: [96] Maga Péter, 2004-10-28 21:58:36

[96] Maga Péter

2004-10-28 21:58:36

Kösz, Betty, a példákat! Azt hiszem, az 1. feladatnál a feladatod szövege nem vág össze BrickTop végeredményével. Biztos, hogy ez a feladat? Illetve biztos, hogy ez a végeredmény?

Egyébként kinek hogy sikerült?

Előzmény: [93] lorybetti, 2004-10-28 20:26:49

[95] tassyg	2004-10-28 20:45:22
Nem tudja valaki, hogy idén is fent lesznek-e az OKÉV oldalán a hivatalos megoldások?

[92] BrickTop	2004-10-28 20:26:49
A megoldás $a_n=2-\sum_{i=1}^n\frac{i}{(i+1)!}$ ?
Előzmény: [91] lorybetti, 2004-10-28 20:14:24

[93] lorybetti

2004-10-28 20:26:49

2. feladat

Az ABCD konvex négyszög csúcsai egy körön vannak. A szomszédos oldalak felezőpontjait összekötő szakaszok a négyszögből négy háromszöget vágnak le. Igazoljuk, hogy e négy háromszög körülírt körei egy ponton haladnak át!

3. feladat

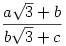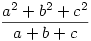Az a, b, c olyan pozitív egészek, melyekre az $\frac{a\sqrt3+b}{b\sqrt3+c}$ tört értéke racionális szám. Bizonyítsuk be, hogy $\frac{a^2+b^2+c^2}{a+b+c}$ egész szám!

4. feladat

Az ABC háromszög beírt körének középpontja O. Az OAB OBC, OCA háromszögek súlypontjai rendre C^', A^',B^'. Igazoljuk hogy AA^', BB^', CC^' szakaszok egy ponton mennek át!

5. feladat

Igazoljuk, hoyg 102 db pozitív egész szám közül kiválasztható kettő úgy, hogy azok különbsége vagy összege osztható legyen 200-zal!

[91] lorybetti

2004-10-28 20:14:24

1. feladat

Az a_n sorozatot (n természetes szám) a következőképp értelmezzük:

a₀=0 és a_n= 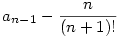$a_{n-1} -\frac{n}{(n+1)!}$ ha n>0.

Adjuk meg a_n-t n függvényében!

[90] Maga Péter	2004-10-28 20:01:04
Igen, van rá igény!
Előzmény: [89] lorybetti, 2004-10-28 19:33:06

[89] lorybetti

2004-10-28 19:33:06

ma volt a gimisek 1. fordulója

nem ártana beírni a feladatokat...persze, csak ha igény van rá

[88] Csillag

2004-08-03 21:25:40

OKTV eredmények

no comment

Előzmény: [86] Csóka Endre, 2004-05-02 22:33:16

[87] Kritya3	2004-05-24 18:38:41
Engem az érdekelne, hogy mivel jövőre más jellegű feladatok lesznek az érettségin, a Matek OKTV-n is lehet-e számítani valamilyen változásra?

[86] Csóka Endre	2004-05-02 22:33:16
Nem tudja valaki az OKTV eredményeket? Az Oktatási Minisztérium honlapjára ugyanis még mindig nem tették fel.

[85] zorbb

2004-03-21 11:07:39

Üdv mindenkinek!

(Bár ez nem oktv de mégis matekverseny) Akik írtak kengurut azoknak hogy sikerült? A megoldókulcs megtalálható a www.zalamat.hu oldalon.

[84] nadorp

2004-03-10 10:00:50

OKTV III/2. megoldásvázlat:

Ha k=2^rk₀,ahol k₀ páratlan, akkor 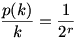$\frac{p(k)}k=\frac1{2^r}$ , ezért

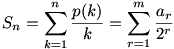$S_n=\sum_{k=1}^{n}\frac{p(k)}k=\sum_{r=1}^{m}\frac{a_r}{2^r}$ , ahol m=[log₂n]

Itt a_r értéke annyi, ahány olyan szám van 1-től n-ig, amelynek a 2^r pontos osztója. Így könnyen látható, hogy $a_r=\left[\frac{n}{2^r}\right]-\left[\frac{n}{2^{r+1}}\right]$ , ezért

$S_n=\sum_{r=0}^{m}\left({\left[\frac{n}{2^r}\right]-\left[\frac{n}{2^{r+1}}\right]}\right)\frac{1}{2^r}=n+\left[\frac{n}{2}\right]\left(\frac12-1\right)+\left[\frac{n}{4}\right]\left(\frac14-\frac12\right)+ ...+ \left[\frac{n}{2^m}\right]\left(\frac1{2^m}-\frac1{2^{m-1}}\right)=n-\sum_{r=1}^{m}\left[\frac{n}{2^r}\right]\frac1{2^r}$

Az alsó becsléshez elég felhasználni, hogy $\left[\frac{n}{2^r}\right]\le\frac{n}{2^r}$ és a mértani sorozat összegképletét

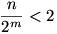
A felső becsléshez felhasználjuk, hogy $\left[\frac{n}{2^r}\right]\ge\frac{n}{2^r}-\frac{2^r-1}{2^r}$ , megint a mértani sorozat összegképletét és végül, hogy $\frac{n}{2^m}<2$

Előzmény: [75] Csillag, 2004-03-04 17:39:09

[83] Adus

2004-03-09 22:31:07

Sziasztok! Nagyon megköszönném, ha az OKTV III. kategória 2. és 3. feladatának megoldását közreadnátok.

Köszönöm!!!

Előzmény: [75] Csillag, 2004-03-04 17:39:09

[82] Kós Géza	2004-03-05 14:54:06
Szerintem jó a megoldásod.
Előzmény: [81] lorantfy, 2004-03-05 13:58:59

[81] lorantfy	2004-03-05 13:58:59
Sziasztok! Én a III./1. példát elég könnyűnek találom, ha valami gond van az alábbi gondolatmenettel szóljatok: OKTV III./1. megoldásvázlat: Legyen az ABC $\Delta$ legkisebb szöge $\alpha$ $\geq$ 60^o Növeljük az AB és AC oldalakat $\sqrt{2}$ hosszúra (ha rövidebbek). Az ABC $\Delta$ nyilván benne van az így keletkező AEF $\Delta$ -ben. Vegyük fel a kocka egyik oldallapjának oldalain a G csúcsból a $\frac{EF}{\sqrt{2}}$ szakaszokat. Ekkor EF átfogójú derékszögű háromszöget kapunk. $\sqrt{2} \leq EK=FK$ , mivel FK az FKH derékszögű $\Delta$ átfogója, melynek KH befogója $\sqrt{2}$ . EFA és EFK azonos alapú egyenlő szárú $\Delta$ -k. FA $\leq$ FK, így az A pont az EFK $\Delta$ belsejébe esik (vagy megegyezik K-val), amit tartalmaz az egységélű kocka.

Előzmény: [75] Csillag, 2004-03-04 17:39:09

[80] BrickTop	2004-03-04 22:32:36
A 2. feladatot szerintem mindenki meg tudta csinálni. Az 1.-vel lehetett a legtöbb időt elvesztegetni, sokféleképpen neki lehet menni egy ilyen feladatnak. Én nem sokra jutottam, kifejeztem a CY szakasz hosszát ismert adatokból, ezek alapján elvileg megszerkeszthető, dehát ez nem a legideálisabb megoldás :( A 3. feladatot nem(/sem) tudtam megcsinálni, de ezt sajnálom a legkevésbé, mert nem hiszem, hogy eszembe jutott volna ez az ötlet. Ülhetnék rajta egy hétig, akkor se ugrana be. A 3.-ra sok időt se lehetett pazarolni, rögtön látszott rajta hogy vagy beugrik, vagy nem.
Előzmény: [77] tassyg, 2004-03-04 18:35:45

[79] tassyg

2004-03-04 22:31:13

Kedves Endre!

A 2. feladatnál úgy tűnik, Te is figyelmen kívül hagytad, hogy az oldalhosszak különböző egész számok, így a (2;2;3) nem jó megoldás. Nekem elég sok eset vizsgálata után a (6;7;12), valamint a (7;8;9) jöttek ki, melyekre a szorzat egyaránt 504. Becslésekkel és néhány eset kipróbálásával ki lehetett zárni a leghosszabb oldal 12-nél nagyobb értékeit. De azért kíváncsi vagyok, volt-e rá valami "szép" megoldás.

Előzmény: [78] Csóka Endre, 2004-03-04 22:19:46

[78] Csóka Endre

2004-03-04 22:19:46

Sziasztok!

Egy-egy nagyon tömör megoldásvázlat a II. kategóriás feladatokhoz (én túlkoros voltam ehhez, de azért megoldottam):

1. P helyének nyilván lineáris függvénye X és Y pont helye, így az XY vektor is. Ez a két szélső helyzetben az AC, illetve a CB vektor. Ha tehát az XY vektort az A kezdőpontba toljuk, akkor a végpont helye C és D között lineárisan változik, ahol D az a pont, melyre (CB vektor)=(AD vektor). Ekkor nyilván akkor a legrövidebb a szakasz, amikor merőleges CD-re, ami egybeesik a súlyvonallal. Mivel ez az eredeti vektor eltoltja, így a merőlegesség arra is igaz. Az XY vektor ismeretében P szerkesztése pedig triviális.

2. Legyen a harmadolópont az ABC háromszög AB oldalának A-hoz közelebbi harmadolópontja. A területfelezésből következik, hogy az egyenes BC-t 3:1 arányban osztja (2/3 * 3/4 = 1/2). Tehát a kerületfelezésből AB/3+BC/2=CA. Könnyű meggondolni, hogy ez csak úgy lehet, ha 3|AB, 2|BC, és így 2<=CA. AB=3, BC=CA=2 ezért a legkisebb megfelelő.

3. Az 1, 2, 4, 8(, 16) elemek be-, vagy nem beválasztásának megválasztásával a 16, ill. 32 különböző maradék mindegyike előáll, ezzel a részhalmazokat maradék szerint egyenlő csoportokba oszthatjuk. Tehát mindkét oldalon az összes részhalmaz számának 1/16-a áll.

Előzmény: [77] tassyg, 2004-03-04 18:35:45

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32]

Már regisztráltál?
Új vendég vagy?