| [63] Berko Erzsebet | 2021-03-04 02:18:05 |
 Érettségi-könyv. Most lassabban lapoztam végig a könyvet. 2-3 kombinatorikai feladat valóban van benne, de külön fejezet nincs. Írok egyet. Melyik az a, b, c, d, e, f, hat elemmel képezhető helycserélési füzetek 517-ke és hányadik füzet ez: c e a f d b? Ez a Vegyes algebrai feladatoknál van.
|
|
| [62] Róbert Gida | 2021-03-03 00:19:29 |
 Nem találom a könyvet, de kombinatorika van benne, legalábbis úgy emlékszem, meglehetősen alapfeladatok.
"Így azért nem nehéz algebrából nehezebbnek lennie, mint a mai érettséginek."
Ja, mert mi is van a mai érettségiben: gráfelmélet is van, de mindegyik feladatban egy "tételt" kell használni: fokszámok összege páros. Statisztika is van, de óvodás szinten: átlag, módusz, medián, szórás számítás. Nyilván nem egy indiai JEE advanced felvételi, ahol mondjuk 2017-ben a diákok 0.92 százaléka ment át.
|
| Előzmény: [61] Sinobi, 2021-02-27 15:50:16 |
|
|
| [60] Berko Erzsebet | 2021-02-21 05:22:33 |
 Szia, Sinobi!
Nekem megvan a könyv. Több éve kaptam egy kedves ismerősömtől. Ő már sajnos nem él.
A könyvben sem kombinatorika, sem valószínűségszámítás nincs. A tartalomjegyzéket egyébként tudod olvasni az antikvarium oldalon. Külsőre olyan, mint a Moór-féle fizikapéldatár. Belül: fehér lap, fekete helyett KÉK betűk.
|
| Előzmény: [59] Sinobi, 2021-02-20 15:21:05 |
|
|
|
| [57] Lóczi Lajos | 2010-04-01 22:51:30 |
 Az illető (elsős egyetemista), aki az alábbiakat írta, nem áprilisi tréfának szánta:
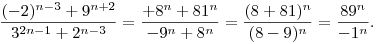
Számomra legviccesebb az utolsó két nevező.
|
|
|
| [55] rizsesz | 2010-01-12 11:45:57 |
 Ez szerintem nem nagyon esett meg, de
26/65-ben egyszerűsítsünk hattal, és lám, mit kapunk: 2/5-öt :)
|
|
| [54] Fálesz Mihály | 2010-01-12 11:06:50 |
 Egy friss elrettentő példa.
(x3/2)2=x9/4
- legalábbis egy vizsgázó szerint.
|
|
| [53] Fálesz Mihály | 2009-12-22 08:47:39 |
 Első Próféta: A gyakorlatvezető feje nagy lesz! És fekete! És minden egyes szeméből egyetemi hallgatók vére fröcsög majd szerteszét! Aztán az egész felsőoktatás felülemelkedik majd, jön a három főből álló MSC, és az egész földkerekség vakítóan kifényesedik, mint egy lakkcipő, vagy ilyesmi!
Második Próféta: Az előadó kezében leend egy nagy, 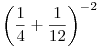 kreditű kard! Mondom, kreditű kard! Mondom, 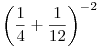 kreditje lesz! Nem kettő, nem öt, nem hét, hanem kreditje lesz! Nem kettő, nem öt, nem hét, hanem 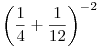 ! Azt lóbálja majd minden, törtet törttel összeadni nem képes nyamvadék feje fölött, akárcsak te ott, uram! ! Azt lóbálja majd minden, törtet törttel összeadni nem képes nyamvadék feje fölött, akárcsak te ott, uram!
Harmadik Próféta: Zebedeus jön a szakállamtitkárával, és azt fogják majd rebesgetni, hogy elhanyagolták a dolgokat. És hatalmas zűrzavar lesz, hogy hol vannak valójában az epszilonok, és senki nem fogja tudni, hová lettek azok a kis bigyók, meg az a fura kis izé, egz... egzisztenciális kvantor vagy mi, amihez hozzá voltak erősítve. És akkor majd a barát elveszíti a barátja helyett megírt beadandó házi feladatát, és a fiatal nem fogja tudni, hogy hol vannak... már azok a dolgok, amiket a tavalyról megmaradt másodévesek birtokoltak, mert a másodévesek csak előző este hagyták ott a kollégiumi buliban este nyolc körül.
(Bocs' az offért...)
|
| Előzmény: [52] Fálesz Mihály, 2009-12-22 06:35:14 |
|
|
| [51] Lóczi Lajos | 2009-12-21 22:33:05 |
 Annak idején azt hittem, hogy ilyen típusú hibát egyetemista diák nem tud felülmúlni. Tévedtem. Íme.
Feladat. Oldjuk meg a valós számok halmazán a
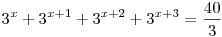
egyenletet.
A megoldás.
3x+3x+1+3x+2+3x+3=3-40
Az exponenciális függvény szigorú monotonitása miatt:
x+x+1+x+2+x+3=-40
4x+6=-40
4x=-46
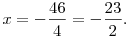
[Nagyon tetszik az illető gondolatmenetében, ahogy elszöszmötöl a végén a törtekkel, miután a kitevőkkel olyan nagyvonalúan elbánt :-)]
|
| Előzmény: [2] Lóczi Lajos, 2008-01-06 02:15:50 |
|
| [50] Mumin | 2008-03-31 01:27:01 |
 Nem hinném, hogy egy diák bárhol, pl. egy zh-ban olyan nevet próbálna leírni, ami nem szerepelt a táblán és nem biztos az írásmódjában. Legalábbis matekos tárgyakból.
A kiejtés pedig jó módszer az előadáslátogatás mérésére a szóbeli vizsgák alkalmával :) (máseróni vagy mászkeróni az a Mascheroni, pláne ha a tétel társnévadójának németes (dán) neve van)
|
| Előzmény: [47] Gubbubu, 2008-03-24 19:32:42 |
|
| [49] PPP | 2008-03-25 21:31:08 |
 "Mondjuk. Nem tartom valószínűleg, hogy letörne a keze emiatt, vagy más baj érné."
Szerintem ilyenkor a tanár fel is írja Riemann nevét a táblára. (Persze nem külön, csak pl. a "Riemann-integrál" cím részeként.)
"De ha >>nem látja<< leírva, mert a tanár nem tölt el ezzel két percetz, akkor ...?"
Ez inkább csak akkor fordulhat elő, ha a tanár csak megemlíti valakinek a nevét, nem kulcsfontosságú definícióban/tételben szereplő névnél. Ilyenkor a diák - ha nem teljesen biztos a hallott név helyes írásmódjában - jelentkezhet, és megkérdezheti, hogyan kell írni. :)
|
| Előzmény: [47] Gubbubu, 2008-03-24 19:32:42 |
|
| [48] Willy | 2008-03-24 20:21:37 |
 Nem akarok nagyon belefolyni a vitába, de... tanár elmondja az órán, hogy "Rííííman", diák meg otthon jegyzetben vagy neten (wikin) megnézi, hogy Riemann. Különben is, az én tapasztalatom azt mutatja, hogy ha a név félteérthető, és a tanárnak is eszébe jut ez, akkor elmondja (főleg, ha a diákok közül valaki megkérdezi, hogy "Elnézést Tanár Úr, akkor most Miman?")...
|
| Előzmény: [47] Gubbubu, 2008-03-24 19:32:42 |
|
| [47] Gubbubu | 2008-03-24 19:32:42 |
 "Miért, mit kéne tennie az egyetemi tanárnak? Mondjuk előadáson felírni hatalmas betűkkel a táblára, hogy RIEMANN, és 10 percig magyarázni, hogy bár "ríman"-nak ejtjük, mégis így írjuk?"
Mondjuk. Nem tartom valószínűleg, hogy letörne a keze emiatt, vagy más baj érné.
"Ahhoz szerintem semmiféle matematikatörténet-ismeret, meg nyelvtudás, meg értelmiségi családból való származás stb nem kell, hogy legyen annyi intelligencia valakiben, hogy ha már látja előadáson/jegyzetben/bárhol a "Riemann" szót leírva, akkor utána talán ne kiejtés szerint írja le."
De ha >>nem látja<< leírva, mert a tanár nem tölt el ezzel két percetz, akkor ...?
"de szerintem a diákok többségének hozzáállásával van a legnagyobb baj."
Kétségtelen, hogy sokszor azzal is baj van, de a tanárnak nem feladata ezt fokozni.
|
| Előzmény: [44] ágica, 2008-01-13 11:41:01 |
|
|
| [45] lgdt | 2008-02-01 04:49:13 |
 Ehhez annyit fűznék hozzá, hogy a BME-n magyarul sem tudnak helyesen írni. A legjellegzetesebb, hogy az összetett szavakat különírják. Az oktatás minősége pedig az ELTÉ-hez képest sehol sincs, teljesen komolytalan az egész (onnan tudom, hogy mindkét egyetemre járok). Bocsánat, ha ez nagyon offtopic, de kikívánkozott belőlem.
|
| Előzmény: [37] Euler, 2008-01-11 21:52:42 |
|
| [44] ágica | 2008-01-13 11:41:01 |
 Miért, mit kéne tennie az egyetemi tanárnak? Mondjuk előadáson felírni hatalmas betűkkel a táblára, hogy RIEMANN, és 10 percig magyarázni, hogy bár "ríman"-nak ejtjük, mégis így írjuk? :) Ahhoz szerintem semmiféle matematikatörténet-ismeret, meg nyelvtudás, meg értelmiségi családból való származás stb nem kell, hogy legyen annyi intelligencia valakiben, hogy ha már látja előadáson/jegyzetben/bárhol a "Riemann" szót leírva, akkor utána talán ne kiejtés szerint írja le. Lehet, hogy a tanárok hozzáállása sem jó sok esetben (bár nekem egyáltalán nincsenek ilyen rossz tapasztalataim, mint amikről te írsz..), de szerintem a diákok többségének hozzáállásával van a legnagyobb baj.
|
| Előzmény: [43] Gubbubu, 2008-01-12 17:23:58 |
|
| [43] Gubbubu | 2008-01-12 17:23:58 |
 A magyartanárnak az a szakmája, hogy háborogjon és megtanítsa helyesen. Nos, itt a jó kis kérdés: az egyetemi tanárnak csak az a szakmája, hogy háborogjon, vagy ha már háborog, akkor tesz is lépéseket a javítás érdekében? Én úgy tapasztaltam, az egyetemi tanár megmarad a háborgásnál, és így egy kicsit arra az emberre emlékeztet, aki húzogatja a kolbászt a kutya orra előtt, majd, ha az beleharap, jól megveri.
|
| Előzmény: [39] Lóczi Lajos, 2008-01-11 22:25:33 |
|
|
|
| [40] Willy | 2008-01-12 01:36:55 |
 Elnézést a gonoszkodó hozzászólásért, de senki se tanuljon nyelvet azért, hogy "nyelvzseni" legyen, mindenki saját magának tanuljon, ne más miatt...
Másrészt, a (nagyarcú) BME-n csak azért fontos az idegen nyelv ismerete, mert a (minőségi) szakirodalom egy része, a felsőbb években csak angolul létezik, ez köztudott. Másrészt lényeges szempont, hogy a hallgató, külföldön képes legyen elhelyezkedni bármilyen témában, nyelvi korlátai ne legyenek.
Egyébként visszatérve az eredeti témához, elég baj, hogy ilyen szánalmas az érettségi, de a legtöbb kisdiák persze örül ennek (Naná, a kamutantárgyak mellett nem kett annyit tanulni, lehet játszani és bulizni...). "A mai fiatalok", (mondhatjuk) nem akarnak jó szakemberek lenni és nem érdekli a legtöbbjüket, hogy tisztességesen végezzék a munkájukat, mivel ez a tömegtermelés miatt egyre kevésbé feltétel. Sőt, olyan butuskák, hogy észre sem veszik, hogy ezzel tönkreteszik magukat... No és ki a felelős? Kik azok, akik szólhatnának, de nem tették elég korán, most meg itt keseregnek? Mi, az értelmiségi réteg! Mi látjuk, hogy mi folyik itt, és ha biztosak is vagyunk a dolgunkban, mikor fogunk össze és teszünk valamit?
|
| Előzmény: [37] Euler, 2008-01-11 21:52:42 |
|
|
