| [60] lorantfy | 2010-12-25 23:46:34 |
 Egy fgv. differenciálható egy adott helyen, ha a differencia hányadosnak létezik határértéke az adott helyen és az véges. A határérték meg akkor létezik (röviden) ha van véges bal- és jobb oldali határértéke és azok egyenlők.
Szóval jóra gondoltál: A fgv. az x=1 helyen nem differenciálható, hiszen a differenciálhányados bal és jobb oldali határértéke ebben a pontban nem egyenlő, tehát ebben a pontban nem létezik a differenciálhányados.
De gondolom, azóta már régen megírtad ebből a ZH-t, amiben egy szakaszonként változó, paraméteresen megadott függvényt kellett differenciálhatóvá tenni a paraméterek megadásával. Legalább is ilyet szoktak adni.
(Legközelebb, ha szünetet tartasz, kérlek, velünk ne közöld, hogy az milyen szünet volt! Köszönöm!)
|
 |
| Előzmény: [59] ga.bakonyi, 2010-10-16 22:39:42 |
|
| [59] ga.bakonyi | 2010-10-16 22:39:42 |
 Még egyszer Üdv mindenkinek!
Tartottam egy rövid cigiszünetet, és közben rájöttem, hogy az előbb az első esetben alaposan összekevertem a feladatmegoldást egy lehetséges ellenőrzéssel. Amit először gyárottam, az az f(x)derivált függvénye, aminek a helyettesítéai értéke 4 ill. 3 a megfelelő heyen. Tehát ezeknek kell lenni a határértékeknek, amiket a tulajdonképpeni feladatmegoldásnál kaptam. Tudtam, hogy nem stimmel valami, de azt nem gondoltam, hogy így össze tudok keverni fontos fogalmakat. Szégyellem magam:) Elnézést a zavarásért. Ha egyéb hiba is van, szépen kérem jellezzék. Még egyszer köszönöm.
|
|
| [58] ga.bakonyi | 2010-10-16 22:05:25 |
 Üdv! Kicsit belekeverdtem a következő példába:
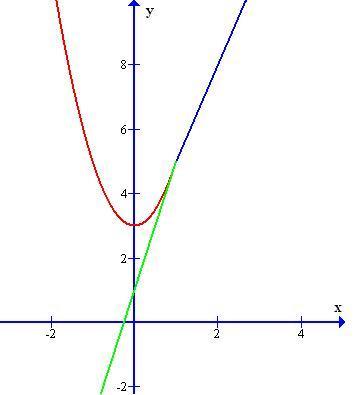
"Írja fel az f(x) függvány a=1 helyhez tartozó d(x) differenciahányados függvényét és számítsa ki d(x)féloldali határértékeit az az a=1 helyen! Differenciálható-e a függvény az a=1 pontban?"
2x*x+3, ha x<=1 ; f(x)=
3x+2, ha x>1
Mo:
A problémám az a=1 hely kitétellel van. Enélkül azt mondanám, hogy
d(x)= 4x, ha x<=1 ;
3, ha x>1
Ebben az esetben d(x) bal oldali határátéke 4, a jobb pedig 3, mivel nem egyenlőek, a függvény nem dif-ható a=1 ben.
De mivel tőlem az 1 helyhez tartozó differenciahányadost kérték, megfordult a fejemben, hogy nem-e a definíció szerinti felírást akarták itt rajtam számon kérni. Kérdés: Van értelme a következőnek:
d(x)= (2x*x-2)/x-1 = 2x+2, ha x<=1 ;
(3x-3)/x-1= 3, ha x >1
Ezeket az f(x)-f(a)/x-a alakból szültem egy kis átalakítással, meg egyszerűsítéssel, de itt nem volt türelmem részletezni.
A határértékek: balról:4 jobbról 3, tehát ugyanaz a válasz, hogy nem dif.-ható a függvény, mert a két határérték nem egyezik meg.
Egyébként a grafikonokból is látszik, az f(x)-nek töréspontja van a=1 ben, tehát nem "sima", d(x)-nek pedig akkora a szakadása, mint egy nagy ház. (Eredetileg az ábrázolás is kérdés volt, de azt még úgy sem tudom ide tenni, mint a szép matematikai jelöléseket.)
Szóval, elvileg ugyanazt kaptam, bárhogy próbálkoztam, de ez az intervallummal való megadás nekem gyanús. Akárhogy is, nem tetszik a megoldásom, nem tudom megfogalmazni, de szerintem valami hatalmas koncepcionális hibát vétettem. Szeretném kérni, hogy aki ráér,ellenőrizzen és legyen szíves írja meg, hol vétettem. Rossz előérzetem van a példával kapcsolatban, és ha a zh-ban derül ki, lehet, hogy késő lesz...
Köszönöm
|
|
|
| [56] SmallPotato | 2010-01-19 15:11:37 |
 Hát azért ez nem "rögtön az eleje". Legalábbis nem a differenciálszámításnak.
Ha jól látom, az egyenletedben érdemes lenne egy új változót bevezetni.
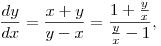
ahonnan pl
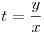
helyettesítéssel egyrészt
y=tx,
másrészt
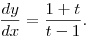
Ez utóbbiba (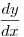 helyébe) az y=tx függvény differenciálhányadosát beírva az eredmény (t-re) elemi módon adódik. helyébe) az y=tx függvény differenciálhányadosát beírva az eredmény (t-re) elemi módon adódik.
|
| Előzmény: [54] vaszil1, 2010-01-19 11:14:20 |
|
|
| [54] vaszil1 | 2010-01-19 11:14:20 |
 Sziasztok. új vagyok itt de látom, hogy vágjátok a differenciálszámítást. Én is megpróbálkoztam vele, de rögtön az elején elakadtam. Az egyenletem a dy/dx=(x+y)/(y-x) volt. Már többféleképpen is megpróbáltam megoldani, de sehogy sem tudom. Kérlek segítsetek.
|
|
|
| [52] Cogito | 2010-01-09 22:59:24 |
 Az (1)-re adott válaszhoz:
Az ötlet jó. Esetleg képlettel is meg tudna adni valaki egy ilyen függvényt?
A (2)-re adott válaszhoz:
Hát igen. Ezt a feladatot azért tettem fel, mert rokonságot mutat az Érdekes matekfeladatok [3129]-es feladatával. Így nem véletlen, hogy az ott talált megoldások némelyike itt is felbukkanhat. (Van ott még valami, ami szintén ül itt is ... .) Ha már ennyi bőrt lehúztunk, húzzunk le még egyet: (2)-re adható ugyanis egy további, az Érdekes matekfeladatok/[3136]-tól különböző megoldás is ... .
|
| Előzmény: [49] jonas, 2010-01-09 16:40:56 |
|
|
|
| [49] jonas | 2010-01-09 16:40:56 |
 A (2)-re igen a válasz. Ugyanaz az indoklás, mint az Érdekes matekfeladatok [3136] hozzászólásban: ha a deriváltnak van a végtelenben határértéke, és az nem nulla, akkor az eredeti függvény határértéke végtelen.
Az (1) nyilván nem igaz, a függvény tarthat a végtelenben A-hoz olyan hullámos módon, hogy a deriváltja nem konvergens. Mondjuk a függvény legyen cikcakkos, felváltva 1 és -1 meredekségű egyenesekből áll, beszorítva két nullához tartó függvény közé, csak a sarkok legyenek lesimítva egy kicsit.
|
| Előzmény: [46] Cogito, 2010-01-09 15:07:09 |
|
|
|
| [46] Cogito | 2010-01-09 15:07:09 |
 Legyen f az (a, ) intervallumon értelmezett differenciálható függvény és tegyük fel, hogy az ) intervallumon értelmezett differenciálható függvény és tegyük fel, hogy az
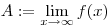
határérték létezik és véges.
(1) Igaz-e, hogy 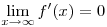 ? ?
(2) Ha (1)-re nemleges a válasz és feltesszük, hogy a
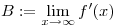
határérték létezik és véges, igaz-e, hogy B = 0?
|
|
| [45] jonas | 2009-02-13 17:38:24 |
 Az egész a láncszabály miatt van. Képzeld azt, hogy a differenciálegyenletedben, ami legyen például dy=y.dx, az y függő változó és az y régi független változó valójában mindketten egy t paramétertől függenek. Jelentse dy az y deriváltját t függvényében, és dx az x deriváltját a t függvényében. Mármost úgy kell képzelni, hogy ez a paraméterezés lényegtelen, tehát tetszőlegesen meg lehet változtatni. Ha egy másik paraméterezésre térnél át, akkor a t szerinti deriváltak megváltoznának ugyan, de az arányuk (bármilyen rögzített pontban) nem változna. Ezért aztán a differenciálegyenletben nem szerepelhet olyan, hogy mondjuk dy=5, mert nem invariáns a paraméterezésre. Mármost ha így képzeled el az egyenletet, akkor végigoszthatsz dx-szel, és a láncszabály miatt dy/dx épp annak a függvénynek a deriváljta, ami y-t adja meg x függvényében. Azt is megtehetnéd viszont, hogy dy-nal osztassz le, és az y-t tekinted független változónak: az így kapott differenciálegyenletnek ugyanaz az (x,y) pontokból álló görbe a megoldása, csak ha most a megoldást úgy írod fel, hogy az x-et adod meg az y függvényében, akkor épp az inverzét kapod annak a megoldásnak, amit az előbb kaptál. (Lehet persze gond abból, ha dx vagy dy valahol nulla.)
|
| Előzmény: [41] Kovacs Bela, 2009-02-12 12:54:02 |
|
| [44] Lóczi Lajos | 2009-02-12 21:33:40 |
 Általában egy fizikai modellből származtatod a differenciálegyenletet, lásd pl. a
http://banach.millersville.edu/~bob/math161/Modeling/main.pdf
első pár sorát, vagy a
http://mintaka.sdsu.edu/GF/explain/atmos_refr/diff_eq.html
oldal ábráját. Itt van szükséged a "kicsi" változásokra, amelyekkel aztán 0-hoz tartunk.
|
| Előzmény: [41] Kovacs Bela, 2009-02-12 12:54:02 |
|
|
| [42] SmallPotato | 2009-02-12 20:43:12 |
 Biztosan találkoztál azzal az interpretációval, hogy pl. a határozott integrált, mint függvénygörbe alatti területet, téglalapterületek összegével közelítjük. A független változó (itt x) tengelye mentén a függvény vizsgált tartományát felosztjuk "kicsi" részekre, ezek szélessége mondjuk  x, és képezzük azon téglalapok területének összegét, amelyek szélessége ezen x, és képezzük azon téglalapok területének összegét, amelyek szélessége ezen  x, magassága pedig a mindenkori f(x). Ha mármost a felosztás finomításával (azaz x, magassága pedig a mindenkori f(x). Ha mármost a felosztás finomításával (azaz 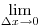 esetén) e területösszegnek létezik határértéke, akkor ez épp a keresett határozott integrál. Ekkor azonban nem beszélhetünk véges (nem-0) esetén) e területösszegnek létezik határértéke, akkor ez épp a keresett határozott integrál. Ekkor azonban nem beszélhetünk véges (nem-0)  x-ekről, hanem jelezni kívánjuk: ezek a szakaszok 0-hoz tartó határértékek. Ezért nem x-ekről, hanem jelezni kívánjuk: ezek a szakaszok 0-hoz tartó határértékek. Ezért nem  x-szel, hanem dx-szel jelöljük őket. Az x-szel, hanem dx-szel jelöljük őket. Az 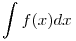 jelölés tartalma (ahol az integráljel alakja nem véletlenül egy elnyújtott S betű, a szummát sugallva) gyakorlatilag egy téglalapterület-összeg: jelölés tartalma (ahol az integráljel alakja nem véletlenül egy elnyújtott S betű, a szummát sugallva) gyakorlatilag egy téglalapterület-összeg: 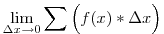 . .
Ha a differenciahányadosra, majd a differenciálhányadosra gondolsz, az értelmezés hasonló. A 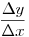 mint differenciahányados két véges (nem-0) szám hányadosa; a mint differenciahányados két véges (nem-0) szám hányadosa; a 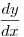 szimbólum mint differenciálhányados már nem valódi hányados, hanem az előbbinek határértéke, ha szimbólum mint differenciálhányados már nem valódi hányados, hanem az előbbinek határértéke, ha 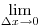 . .
|
| Előzmény: [41] Kovacs Bela, 2009-02-12 12:54:02 |
|
|
| [40] Lóczi Lajos | 2009-02-11 23:55:39 |
 Formálisan ossz le dx-szel, és ahol dy/dx-et látsz, cseréld ki y'(x)-re; vagyis
xy2(x)+y(x)+(x2y(x)-x)y'(x)=0.
(Ha pedig dy-nal osztottál volna le, akkor az y(x) megoldás x(y) inverzére kapnál egy differenciálegyenletet.)
|
| Előzmény: [39] Kovacs Bela, 2009-02-11 20:34:26 |
|
| [39] Kovacs Bela | 2009-02-11 20:34:26 |
 Még a suliban nem tanultunk differenciálszámítást. De utánaolvastam a dolgoknak, és tudom, hogy mi az a deriválás, meg az integrálás. Azonban azt nem tudom megérteni, hogy mit jelent amikor a differenciál egyenletben dx-et, vagy dy-t írunk egy sima kifejezés végére. Pl.:
(xy2+y)dx+(x2y-x)dy=0
|
|
|
| [37] Euler | 2009-01-22 23:33:56 |
 Használd az addiciós összefüggést, sinx négyzete=( 1- cos2x)/2, ezt beirva már egyszerű, mert sin2x-cos2x értékkészlete kell valójában, ezt pedig megegyezik gyök2. sin(2x-45 .), innen már menni fog.
|
| Előzmény: [35] j.milan, 2009-01-22 21:03:58 |
|
|
