Fórum: Ötletadó topik

[1] [2] [3]

Szeretnél hozzászólni? Jelentkezz be.

[20] Vonka Vilmos Úr

2010-04-18 09:58:50

Úgy tűnik, valóban elírás történt mindkét esetben. Lásd:

http://db.komal.hu/scan/1991/11/99111347.g4.png

http://db.komal.hu/scan/1991/11/99111348.g4.png

Előzmény: [19] Sophie, 2010-04-18 08:18:50

[19] Sophie

2010-04-18 08:18:50

Megint egy kis segítség kéne:

A versenyvizsga portál szerint:

OKTV 1990/1991. 1. kategória 1. forduló 2. feladat:

Oldjuk meg a következő egyenletrendszert a valós számok halmazán:

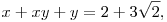
$x+xy+y=2+3\sqrt2,$

x²+y³=6.

Ugyanitt az 5. feladat:

Oldjuk meg a pozitív egész számok halmazán az

x³-y²=4p

egyenletet, ha p prímszám!

Azt mondja Vica néni, szerinte itt valami elírás van. Úgy gondolja, az első esetben az x²+y²=6 lenne a második egyenlet helyesen, főleg, hogy 2. feladatról van szó, tehát nem kellene túl bonyolultnak lennie. A második esetben pedig szerinte az x²-y²=4p akart lenni a kérdéses egyenlet.

Mit szóltok?

[18] Sophie

2010-04-13 08:29:06

Hát ez az utolsó példa még nekem is megtetszett!:)) Még kicsit gondolkozik, minden oldalról látni akarja. Mindenesetre köszönjük mindannyiótoknak.

(OKTV példák tizenegyedikes unoka tréningezése kapcsán kerültek elő. Sajnos nem lett harmadik fordulós egy pont híján, de a lelkesedés nagy lett. )

[17] Sophie	2010-04-13 08:15:17
Kötelességem lenne elmesélni, micsoda örömet szerzett ez az ötletadás. Teázgatás közben szépen végig gondolta azt az első mondatot, és - azt mondja - szépen igazolódott is az állítás. Dehát Ön biztos jobban szavakba tudná ezt önteni, mármint hogy mennyire lehet az ilyesminek örülni.:) Én meg annak örülök, hogy örül.
Előzmény: [12] Vonka Vilmos Úr, 2010-04-11 17:42:10

[16] béjé

2010-04-13 00:21:40

Szép jó estét!

A másik egyenlőtlenséget is hasonlóan lehet megmutatni: Tekintsük a háromszögünket a,b,c oldalakkal, R jelölje a háromszög köré írt kör sugarát.

Használjuk, hogy: a=2Rsin $\alpha$ , b=2Rsin $\beta$ , c=2Rsin $\gamma$ , ahol R a háromszög köré írt kör sugara.

Kellene, hogy:

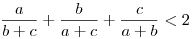
$\frac {a}{b+c} + \frac {b}{a+c} + \frac{c}{a+b} < 2$

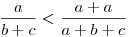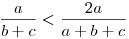A háromszög-egyenlőtlenség alapján b+c>a, ez ahhoz kell, hogy $\frac {a}{b+c} < \frac {a+a}{a+b+c}$ . Utána adódik, hogy $\frac {a}{b+c} < \frac {2a}{a+b+c}$ . A másik két tagra ugyanígy, az összegre így a felső becslés 2.

Előzmény: [13] Sophie, 2010-04-12 19:06:54

[15] psbalint	2010-04-12 22:43:58
ennél gyengébb, ám jelen esetben épp megfelelő alsó becslést kapunk akkor is (és ez a megoldás talán egyszerűbb), ha a nevezőkhöz sorban hozzáadunk sin alfát, sin bétát és sin gammát, így a közös nevező miatt épp egyet kapunk. mivel a nevezőkhöz pozitív számokat adtunk, csökkentettük az eredeti kifejezést, ami így biztos hogy nagyobb, mint egy.
Előzmény: [14] Fálesz Mihály, 2010-04-12 22:12:02

[14] Fálesz Mihály

2010-04-12 22:12:02

A Nesbitt-egyenlőtlenség szerint ha a,b,c>0, akkor

$\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b} \ge \frac32.$

(Számtani-harmonikus az a+b, a+c, b+c számokra.)

Előzmény: [13] Sophie, 2010-04-12 19:06:54

[13] Sophie

2010-04-12 19:06:54

Köszönöm Vilmos a kedvességét, lekötelez!:)

Úgy gondolom, ötletadásként az első mondatát fogom felolvasni az illető hölgynek (ha megjön a sétából), és persze ha azt mondja, ennyi elég lesz.

Közben újabb feladatba bonyolódtunk szombaton:

OKTV 1990. 1. kategória 2. forduló, 3 feladat:

Igazolja, hogy $\alpha$ , $\beta$ és $\gamma$ egy háromszög szögei, akkor

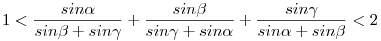
$1<\frac{sin\alpha}{sin\beta+sin\gamma}+\frac{sin\beta}{sin\gamma+sin\alpha}+\frac{sin\gamma}{sin\alpha+sin\beta}<2$

Előzmény: [12] Vonka Vilmos Úr, 2010-04-11 17:42:10

[12] Vonka Vilmos Úr

2010-04-11 17:42:10

Jelölje pl. az AEC szöget $\alpha$ . Írjuk fel az ABC háromszög AC oldalára és a CDE háromszög CE oldalára a koszinusztételt, majd ezek alapján az ACE háromszögre a Pitagorasz-tételt. Kihasználva, hogy ABCE és ACDE húrnégyszögek, továbbá, hogy ACE derékszögű, a fellépő szögek mindegyike kifejezhető $\alpha$ segítségével. Így a következő összefüggést kapjuk:

4=a²+b²+c²+d²+2abcos $\alpha$ +2cdsin $\alpha$ .

Mivel az ACE háromszöget tekintve 2cos $\alpha$ a CE oldal hossza, adódik, hogy 2cos $\alpha$ >c (hiszen a CE ív hosszabb, mint a CD ív). Hasonlóan, 2sin $\alpha$ az AC oldal hossza, így 2sin $\alpha$ >b. Ezeket behelyettesítve a fent nyert összefüggésbe, adódik az állítás.

Előzmény: [11] Sophie, 2010-04-07 07:11:14

[11] Sophie

2010-04-07 07:11:14

Most látom, már megint nem jó a link. Akkor (csak azok kedvéért, akik szintén lusták mindig előszedegetni a feladatot):

Az AE egységsugarú félkörön adottak az AB, BC, CD, DE húrok, amelyeknek a hossza rendre a, b, c, d. (A húrokhoz tartozó köríveknek nincs közös belső pontja.)

Igazoljuk, hogy

a²+b²+c²+d²+abc+bcd<4

Lényeg: megmondtam neki. Azt mondja, van egy olyan érzése, hogy nem szögfüggvény, de azért egyszer már próbálta, nem jutott semmire.

Én mint kibic: nevetségesen egyszerű, ha a Thalesz-tételhez nyúlunk? Persze-persze, aztán mit kezdünk vele?:)

[10] Valezius	2010-04-06 20:57:22
Meglepődnék, ha az oldalakat nem szögfügvénnyel kéne kifejezni. Azon meg mégjobban, ha én is meg tudnám oldani :D

[9] Sophie	2010-04-06 19:43:18
Hát akkor talán próbáljatok együtt gondolkozni! :-)
Előzmény: [8] R.R King, 2010-04-06 19:01:44

[8] R.R King	2010-04-06 19:01:44
Igen, egy másik fórumról idéztem. Ezt a feladatot én is kérdeztem már egyszer, mert elsőre nekem sem jött ki. Az új feladatodat is próbáltam régebben megoldani, elsőre nem tudtam bizonyítani utána meg feledésbe ment. Ez a te matektanárod igen jó érzékkel tud nehezet kérdezni(legalábbis számomra az), illetve olyat ami engem is érdekel:)
Előzmény: [7] Sophie, 2010-04-06 18:13:22

[7] Sophie

2010-04-06 18:13:22

Nagyon szépen köszönjük a segítséget. Az első lépés (a négyzetre-emelésig) megvolt, csak azt mondja, nem tudta összekötni .... húúú, nem is próbálom megérteni mit mivel. Szóval sikerült, az a lényeg, elég volt a segítség, köszi! (Vajon R.R.King idézőjele valamely idézett helyet takar?)

És akkor a következő feladat: OKTV1991/1992.1.kategória, 3. forduló, 3. feladat

Azt mondja, próbált sok mindent, de sajnos nem tudta végig vinni egyik módon sem. Szóval mi lenne a segítő ötlet szerintetek?

(Köszi a linkesítést is, igyekszem tanulni ... végül is a Közgázon tanultunk programozást is, Fortrant, az elkészített programot lyukkártyán rögzítették, csak már nem emlékszem, minek ...:))

[6] Sirpi

2010-04-04 17:56:52

Legyen a gyökösszeg q racionális szám. Ekkor 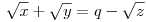$\sqrt x + \sqrt y = q - \sqrt z$

Ezt emeljük négyzetre, és így a sok racionális tag mellett lesz két gyökös tag, amiből kapunk rájuk egy összefüggést. Ugyanezt persze megismételhetjük z helyett bármelyik másik tagra is...

Én így indulnék el. Ha ez kevés, akkor szívesen írok/írunk bővebbet, csak nem akarom egyből lelőni (ja, és a linket "linkesítettem", így kell: \link{http://...}{link szövege} )

Előzmény: [4] Sophie, 2010-04-04 17:02:55

[5] R.R King	2010-04-04 17:48:59
,,Először mutasd meg, hogy ha gyök(x)+gyök(y) racionális, akkor mindkét tag racionális. Utána érvelj indirekten: tegyük fel hogy gyök(x)+gyök(y)+gyök(z) egy r>0 racionális szám, ekkor x+y+2gyök(xy)=r+z-2rgyök(z), vagyis gyök(xy)+rgyök(z) is racionális. Az előző miatt r*gyök(z) is racionális, tehát gyök(z) is az. Ugyanígy gyök(x) és gyök(y) is racionális"
Előzmény: [4] Sophie, 2010-04-04 17:02:55

[4] Sophie

2010-04-04 17:02:55

A link nem sikerült, de a matematikai módra sszem rájöttem. Szóval: OKTV 1991/1992, 1. kategória, 3. forduló 2. feladat:

Bizonyítsa be, hogy ha

x, y, z,

és

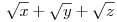
$\sqrt{x}+\sqrt{y}+\sqrt{z}$

racionális számok, akkor

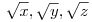
$\sqrt{x}, \sqrt{y}, \sqrt{z}$

mindegyike racionális szám!

---- Mindamellett, hogy tapsot érdemlek, kérem az ötletadó üzeneteket VN-nek! Előre is köszönök minden fáradozást, VN nevében is!

[3] Sophie

2010-04-04 16:49:28

OKTV 1991/1992. 1. kategória 3. forduló 2. feladat..

Asszem a link már sikerült, de a négyzetgyök-parancsot csak matematikai módban szabad használni, amit egyelőre még nem tudok, mi. Elolvasom mégegyszer a TEX minitanfolyamot, mert honnan tudhatnám máshonnan.

[2] Sophie	2010-04-04 16:13:29
Nahát a linket is csak így tudtam ... próbálok tanulni. Sok türelmet hozzánk!

[1] Sophie

2010-04-04 16:12:24

Kedves Fórumozók! Középiskolás matektanárnőm sajnos elvesztette a látását. Egyik kedvenc elfoglaltsága, hogy diktafonra felmondott matekpéldákat old meg - fejben. Hála az internetnek, bőven van feladat, és általában hozzá megoldás is. Néha azonban előkerül olyan feladat, amelyhez nem találok megoldást. Ráadásul nem is az az igazi segítség - Ti ezt persze nálam sokkal jobban tudjátok - ha az ember ismeri a megoldást, hanem ... ő úgy mondja, amig látott, elővett egy csomó könyvet, lapozgatta, és keresett hasonló problémákat, őtletet, mivel próbálkozhatna, meg ilyesmi. Én nem vagyok ebben partner. Tudjátok: - még ha valaha valamennyire is ment az ilyesmi - 25 éve érettségiztem, tök más a munkám, az időtényezőről ne is beszéljünk.

Tehát aki tud, léci segíteni abban, mit mondjak VN-nek pl. ezzel a feladattal kapcsolatosan:

Feladat

(próbáltam az idemásolást, majd legközelebbre kitanulom, hogy lehet a képleteket idetölteni.)

[1] [2] [3]

Már regisztráltál?
Új vendég vagy?