Fórum: Ötletadó topik

A topiknyitó hsz-t olvastad? Ha nem, akkor tedd meg lécci, és ugorj neki a feladatnak - fejben.

Vica néni ugye nem matektanár?

b rész megoldása: x,y,z nemnegatív, így , azaz w=x+y+z jelöléssel , mivel w0 így a másodfokú egyenlőtlenségből (kisebbik gyök negatív): . Továbbá az is kijött, hogy pontosan akkor van itt egyenlőség, ha .

Vica néni azt mondja, annyit gondolkozott, hogy a feladat b.) kérdésében honnan jön a feltétel, de nem jutott eddig eszébe semmi. Esetleg valami ötlet?

Trivi felső becslést adtam, nem mondtam azt, hogy az a maximum.

Vica néni maga is jelezte, hogy miközben ő is rájött erre a megoldásra, más eredményt kapott. Sőt! Arra is rájött, hol lett véletlenül a minuszból plusz. Hiába: vagy negyven évet tanított matekot a közgazdaságiban, ahol könnyen előfordul az ilyesmi.:) Mindamellett HoA megoldását is átbeszélte az unokájával, és tetszett nekik az is.

És akkor most megigérem, hogy többet nem hálálkodom, hanem várom a további két feladathoz a megoldásgondolatébresztőket.

Ne viccelj már, nem a végeredmény?

Ne viccelj már, az egyenletből

Üzenet továbbítva. Köszi.

Ne viccelj már :) sokkal egyszerűbben: a bal oldal 3 négyzetre bontható: x-0,5, y-1 és z-1,5 négyzeteire. Ezek összege a konstansok négyzeteinek bevitelével a jobb oldalra 27/4-et adnak. Négyzetes számtanival kijön, hogy a négyzetek összegének harmada legalább (x-0,5+y-1+z-1,5)/3, innen egy kis átalakítással x+y+z maximuma 7,5.

Ja, hogy csak nem lett jó a link! Pedig úgy igyekeztem!:)

A segítséget pedig máááár továbbítom is.

(Csak mesélem , hogy a JAWS nevű program - ez olvassa fel a nem látóknak, ami a képernyőn van + elmond minden szükséges utasítást is - a képleteket nem érti. Képzelhetitek, milyen vicces leírva, hogy x a négyzeten + ... satöbbi. De ez már alegkevesebb. )

4. feladat Az x, y, z nemnegatív valós számok kielégítik az

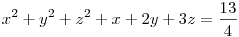
egyenletet.

A) Mekkora az x+y+z összeg maximuma?

B) Bizonyítsuk be, hogy .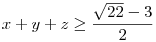

Vegyük észre hogy az egyenlet egy gömb egyenlete. A feltétel értelmében ennek a nemnegatív koordináták térnyolcadába eső részéről van szó. x+y+z=k egymással párhuzamos síkok egyenlete az egyes k értékekre. Az A) feladat a legnagyobb k értékhez tartozó, a gömbbel közös ponttal rendelkező ilyen sík ( érintősík ) megkeresését jelenti.

A B) feladat pedig a legkisebb olyan k érték megkeresésével oldható meg, amelyre x+y+z=k -nak van a gömbnek a nemnegatív térnyolcadba eső részével közös pontja.

Újra: 2002-2003. 2. kategória 2. forduló

Országos Középiskolai Tanulmányi Verseny matematikából 2003/2004 11 - 12. évfolyam 2. kategória 3. forduló

1. feladat

A P pont a hegyesszögű ABC háromszög AB oldalán mozog. A P-n át AC-vel húzott párhuzamos a BC oldalt az X pontban, a P-n át BC-vel húzott párhuzamos pedig AC-t az Y pontban metszi. Adjunk eljárást olyan P pont szerkesztésére, amelyhez tartozó XY szakasz a lehető legrövidebb. Bizonyítsuk be, hogy a legrövidebb XY szakasz merőleges a C csúcsból induló súlyvonalra.

2002-2003. 2. kategória 2. forduló

"... amihez most kérnék ötletet, az a 2002-03 2. kategória 2. forduló 3. és 4. feladat és a 2003-04 2. kategória 3. forduló 1. feladat. Ezek gimis feladatok, köszi szépen."

Azért az idézőjel, mert az ötletadó segítséget váró hölgy kitanulta a vakbarát számítógép használatot teljesen. Sajnos jelen fórum a látássérültek számára nem elérhető, úgyhogy továbbra is én közvetítem a hozzám e-mailben eljuttatott kéréseit.

Úgyhogy - a korábbiakhoz hasonlóan - ha volna valakinek valami ötlete.

:) Már nincs kérdés.

Néha elhamarkodom.

Köszönünk mindent.

Ezek közül semelyik. Ezeket arra a kérésedre írtam, hogy "ehhez hasonló azonosságokból szemezgethetnék neki".

Amit felhasználtunk, azt a [25]-ben már írtad: [24] második mondata. [24]-ben a többi nem azonosság, hanem átrendezés. (Na jó, az (x+y+z)² kifejtését hívhatod azonosságnak.) Szóval nem igazán értem a kérdésed.

Ezer bocsi, de ezek közül most melyik az az azonosság, amit felhasználtunk? :)

Pl.

http://mathworld.wolfram.com/PolynomialIdentity.html

http://mathworld.wolfram.com/EulerFour-SquareIdentity.html

http://mathworld.wolfram.com/FibonacciIdentity.html

http://mathworld.wolfram.com/LebesgueIdentity.html

http://mathworld.wolfram.com/LiouvillePolynomialIdentity.html

http://mathworld.wolfram.com/GausssPolynomialIdentity.html

stb.

Próbáltam keresgélni olyan oldalt ahol ilyen, és ehhez hasonló azonosságokból szemezgethetnék neki, de sajnos nem találtam. Ne is keressem?

Köszönjük szépen. Csak az általad említett azonosságot olvastam fel neki. Mondta, hogy végiggondolja.

Van még a (4,4,-5) is, illetve ezek permutációi.

Használjuk az x³+y³+z³-3xyz=(x+y+z)(x²+y²+z²-xy-xz-yz) azonosságot. Ebből kapjuk, hogy 1-xyz=x²+y²+z²-xy-xz-yz, azaz 1-xyz=(x+y+z)²-3xy-3xz-3yz. Tehát most xy(3-z)=8-3z(x+y), vagyis xy(3-z)+3z(3-z)=8, s így (3-z)(xy+3z)=8. Innen már egyszerű.

Mármint: 2cos2x+cos6x+cos10x=2cos²x=1

1992. 2. forduló második feladat.

Vica néni úgy gondolja, a második egyenlőségjel "-" akart lenni.

Oldjuk meg a következő egyenletet:

2cos2x+cos6x+cos10x=2cos2x=1

Az 5. feladattal is gondja van.

Oldjuk meg az egész számok halmazán a következő egyenletrendszert:

x+y+z=3

és

x³+y³+z³=3

Van ugye a triviális megoldás, az 1, de másikat nem bírt kieszelni. Valami ötlet?

Áááá, kösz! Ez esetben esetleg jelenthetnénk a hibát valakinek.

További szép vasárnapot!