|
|
| [21] Zilberbach | 2013-01-25 14:56:14 |
 Ennek gondolj utána alaposan. Teljesen rossz és zavaros amit írsz.
n3 törzstényezői között mindenképp ott kell hogy legyen a 3, ezt vitatni botorság. A második mondatod is teljesen rossz.
Egyébként pont arról van szó, hogy nem lehet olyan pozitív egész számokat találni amik kielégítenék az eredeti egyenletet.
Elejétől olvas, gondolkodik, ír - ez a helyes sorrend.
|
| Előzmény: [20] Blinki Bill, 2013-01-25 14:44:44 |
|
| [20] Blinki Bill | 2013-01-25 14:44:44 |
 "Vegyük észre, hogy n3 törzstényezői között mindenféleképpen ott kell hogy legyen a 3,."
Ez sajnos nem igaz, mert az eredeti egyenlet bal oldala 3-mal osztva 1 maradékot ad, így n köb nem osztható 3-mal.
|
| Előzmény: [19] Zilberbach, 2013-01-25 14:05:55 |
|
| [19] Zilberbach | 2013-01-25 14:05:55 |
 Legutóbb ott hagytam abba, hogy ha bizonyítani tudnánk azt, hogy a 3t2 + 3t + 1 kifejezés nem lehet köbszám, akkor ezzel bizonyítanánk a Fermat sejtést n=3 esetre.
Írjuk föl a 3t2 + 3t + 1 = n3 egyenletet.
Osszuk el mindkét oldalt 3-mal: t2 + t + 1/3 = n3/3
Vegyük észre, hogy n3 törzstényezői között mindenféleképpen ott kell hogy legyen a 3, és mivel n pozitív egész, ezért n3/3 is egész szám kell hogy legyen. Mivel t is pozitív egész szám, ebből következik hogy t2 + t is egész szám, és ehhez adunk még egyharmadot, tehát a jobb oldal összege nem lehet egész szám.
Ezzel bizonyítottuk, hogy a 3t2 + 3t + 1 = n3 egyenlet nem teljesülhet, ha t és n pozitív egészek.
|
| Előzmény: [18] Nánási József, 2010-08-14 15:08:36 |
|
|
| [17] m2mm | 2010-08-14 14:52:24 |
 http://fermatslasttheorem.blogspot.com/2005/05/fermats-last-theorem-proof-for-n3.html
Korrektnek tűnik.
|
|
|
|
|
| [13] bily71 | 2010-08-14 09:08:48 |
 Általánosan:
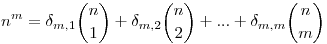
ahol a  m,1 együttható értékét a Goldbach-sejtésről topik [456]-ban adtam meg egy rossz bizonyítás részeként, ezért senki nem figyelt rá. m,1 együttható értékét a Goldbach-sejtésről topik [456]-ban adtam meg egy rossz bizonyítás részeként, ezért senki nem figyelt rá.
m=3 esetén:
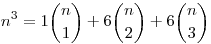
|
| Előzmény: [12] bily71, 2010-08-14 08:53:38 |
|
|
|
| [10] SAMBUCA | 2010-08-13 23:18:15 |
 Nem véletlen, amit észrevettél, ha megnézed, hogy hogyan alakulnak a szomszédos tagok közti különbségek, akkor:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
8 |
27 |
64 |
125 |
216 |
343 |
512 |
729 |
1000 |
1331 |
1728 |
2197 |
2744 |
3375 |
4096 |
|
7 |
19 |
37 |
61 |
91 |
127 |
169 |
217 |
271 |
331 |
397 |
469 |
547 |
631 |
721 |
|
|
12 |
18 |
24 |
30 |
36 |
42 |
48 |
54 |
60 |
66 |
72 |
78 |
84 |
90 |
|
|
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
|
|
Az első sor n3, a második (n+1)3-n3=3n2+3n+1, a harmadik: (3(n+1)2+3(n+1)+1)-(3n2+3n+1)=6n+6, a negyedik pedig: (6(n+1)+6)-(6n+6)=6
a fokszám tehát mindig eggyel csökken
|
| Előzmény: [9] Nánási József, 2010-08-13 21:56:31 |
|
| [9] Nánási József | 2010-08-13 21:56:31 |
 Vegyük azt, hogy egy n egység oldalú kockát hány kockával kell bővíteni, ahhoz, hogy n+1 élű kockát kapjunk.
1+6*(1+2+…+(n-1)+n)=(n+1)3-n3 Bizonyítás teljes indukcióval:
Tegyük fel, hogy k-ra igaz(k élű kocka k+1-re való bővítésére igaz). Ez azt jelenti, hogy 1+6*(1+2+…+k-2+k-1+k)=(k+1)3-k3 (indukciós feltétel)
K=k+1-re is nézzük meg
1+6*(1+2+…+k-2+k-1+k+k+1)=(k+2)3-(k+1)3
(k+1)*6+1+6*(1+2+…+k-2+k-1+k)=(k+2)3-(k+1)3
6*(k+1)+(k+1)3-k3=(k+2)3-(k+1)3
6k+6+k3+3k2+3k+1-k3=(k+2)3-(k+1)3
(k+2)3-3k2-3k-1-k3=(k+2)3-(k+1)3
(k+2)3-(+3k2+3k+1+k3)=(k+2)3-(k+1)3
((k+2)3-(k+1)3=(k+2)3-(k+1)3
Ha megnézzük, akkor n=1-es kocka 1 egységkockából áll, n=2-es kocka, 8 kockából áll,
1+6*(1)=8-1
Tehát, ez igaz minden kockapárra.
Ez azt is jelenti, Hogy (n+1)3-n3=n3-(n-1)3+6n
Ez egy kis szerintem érdekes dolog, amit tegnap úgy vettem észre, hogy Excelben számolgattam dolgokat. Igaziból azt, hogy két kocka közt mekkora a különbség, és ezek különbsége mennyi, és az jött ki, hogy 7;13;19;25...
|
|
| [8] R.R King | 2010-08-13 10:17:50 |
 Ha jól emlékszem ennek a bizonyítása Euler egészek segítségével történik és nem ismerek rá egyszerű elemi megoldást. Szóval szerintem olvass egy kicsit utána ennek pl. a wikipédián, vagy Freud Róbert: Számelmélet című könyvében.
|
| Előzmény: [7] R.R King, 2010-08-13 10:15:16 |
|
| [7] R.R King | 2010-08-13 10:15:16 |
 Az általad megadott egyenlet valóban megoldhatatlan a pozitív egészek körében ez a híres Fermat-sejtés n=3 esete. 1995 óta ez már Wiles-tétel. Tehát be van már bizonyítva, hogy ha n>2 akkor an+bn=cn nem oldható meg pozitív egészekben.
|
|
|
| [5] Zilberbach | 2010-08-13 07:11:10 |
 Igazatok van, meg kell jegyezni, hogy a, b, és c nem lehetnek = 0.
Valamint helyesebb oldal helyett lapot írni egy kocka esetében.
És 0 kockából épített kocka nem kocka (csak ez már nem passzol az óvodás stílushoz).
|
| Előzmény: [2] Nánási József, 2010-08-12 23:18:36 |
|
|
|
| [2] Nánási József | 2010-08-12 23:18:36 |
 Ha a=b=c=0, akkor 03+03=03
Szóval azt ki kell kötni hogy:
a és b  0 0
Persze ezeket csak akkor kell, ha elfogadjuk a nulla egységkockából álló kockát.
ja köböt úgy írsz, hogy amit te is írtál $ közé teszed.
a3=$a^3$
|
|
| [1] Zilberbach | 2010-08-12 22:33:55 |
 A köbszám-sejtés: Nem lehet olyan a, b, c természetes számokat találni, amik kielégítenék az alábbi egyenletet: a^3 + b^3 = c^3
(Sajnos csak így tudom írni a hatványkitevőket.)
Óvodás szinten: Óvodában vagyunk, ahol nagyon sok, azonos méretű kocka van. Ezekből a kockákból építünk nagyobb kockákat. Azt találjuk, hogy ha egy kisebb kockát nagyobbá építünk át - további alapméretű kockák hozzáadásával - majd azt visszabontjuk, akkor a lebontott kockákból soha nem tudunk (maradék nélkül) egy másik kockát építeni. Óvodás szinten így fogalmazható meg a köbszám sejtés.
Általános iskolás szinten: A legkevesebb elemet kívánó kocka-nagyobbítást írjuk föl képlettel, ha a bővítendő kocka éle n számú egységkockából áll:
A három oldal nagyobbítása: 3n^2 darab egység-kockát igényel, a három él bővítése 3n darab egység-kockát, a csúcs bővítése 1 darabot, az összesen: 3n^2 + 3n + 1.
Ha ezt hasonló módon tovább nagyobbítjuk az 3(n+1)^2 + 3(n+1) + 1 darab egység-kocka fölhasználását igényli.
Ha ezt is tovább építjük az további 3(n+2)^2 + 3(n+2) + 1 darab egység-kocka fölhasználását fogja igényelni, és így tovább...
Gimnáziumi szinten: Vegyük észre hogy a(z egymás után következő) minimális számú elemet igénylő bővítések sorozatot alkotnak.
Továbbá vegyük észre azt is, hogy ha bizonyítani tudnánk azt, hogy ennek a sorozatnak az elemeiből tetszőleges kezdő és végző elemmel képzett (sorozat-)összegek, illetve a sorozat elemei önmagukban, soha nem lehetnek köbszámok - akkor bizonyítottuk a köbszám-sejtést.
Egyetemi szinten: Bizonyítsuk a sorozatról tett fönti állítást!
Talán egyszerűbb lenne bizonyítani azt, hogy a 3t^2 + 3t + 1 kifejezés nem lehet köbszám (ahol t = bármely természetes szám), és már azzal is előbbre lennénk a köbszám sejtés bizonyításának (rögös) útján.
Ez az, ami nekem sajnos nem megy, talán azért mert csak egy (régi) közepes matematika érettségivel rendelkezem, de hátha valaki nálam képzettebbnek sikerülne.
|
|
