| [145] ScarMan | 2006-01-21 12:10:33 |
 Beírok egy feladatot én is, elnézést, ha kicsit kacifántosan írtam le (ha vmit rosszul akkor pláne), de nem kellett bele TeX, és legalább népszerűsödik a téma.
B.3862. feladat megoldása:
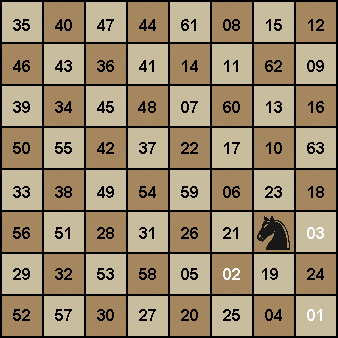
Ismeretes, hogy a sakktáblán végig lehet úgy léptetni egy huszárt, hogy az minden mezőre pontosan egyszer lép rá, és az utolsó mezőről visszatérhet a kezdő mezőre (ld. ábra). Egy ilyen út látható az ábrán. Ez az út 64 lépésből áll, hiszen ennyi a mezők száma. Ha el akarunk helyezni 32 huszárt a mezőkön úgy, hogy azok ne támadják egymást, nem tehetünk két huszárt két, az út során egymást követő mezőre.
Ez azt jelenti, hogy az 1-64 számokból kell kiválasztanunk 32-őt, úgy, hogy semelyik kettő ne legyen szomszédos, és itt a 64-et és az 1-et is szomszédosnak tekintjük. Ezt csak úgy tehetjük meg, ha minden második számot választunk ki. Legalább egy szám ugyanis mindenképp kell legyen két szám között, tehát minden szám után kell hagynunk egy helyet, vagyis egy szám legalább két helyet foglal, így a 32 kiválasztott szám összesen lefoglalja mind a 64-et, ez a legjobb eset, amikor mindenhol egy szám marad ki. Sehol sem marad ki egy számnál több, így ha valahol többet hagynánk ki, a maradékot már nem tudnánk megfelelően elhelyezni.
Minden második számot kétféleképpen tudjuk kiválasztani: vagy a páros számokat, vagy a páratlan számokat. Látható, hogy a huszár mindig a saját mezőjével ellentétes színű mezőt támad, tehát egyrészt az azonos színű mezők nem támadhatják egymást, másrészt a huszár által bejárt út a sakktáblán váltakozó színű mezőkön történik, tehát az azonos paritású lépések azonos, a különböző paritású lépések különböző színűek.
Ez azt jelenti, hogy a két lehetséges kiválasztás: minden fehér, vagy minden fekete mezőre állítunk egy huszárt. Így ezek a huszárok valóban nem fogják egymást támadni, hiszen megegyező színű mezőn állnak.
|
 |
|
| [144] lorantfy | 2006-01-21 00:03:53 |
 Mert a log2(x) fgv. szig. mon. növekvő, tehát nagyobb szám logaritmusa nagyobb.
Így pl. ha x2<2x akkor x2 helyett 2x-t írva a fgv. "hasába" nagyobb értéket kapunk:
x2+log2(x2+2x)<x2+log2(2x+2x)=x2+log2(2x+1)=x2+x+1<2x+x+1
Vagyis x2+log2(x2+2x)<2x+x+1, nem lehet egyenlőség.
És fordítva, ha x2>2x, akkor:
x2+log2(x2+2x)>x2+log2(2x+2x)=x2+log2(2x+1)=x2+x+1>2x+x+1
Tehát x2+log2(x2+2x)>2x+x+1, így sem lehet egyenlőség.
Éppen azt láttuk be, hogy egyenlőség akkor, és csak akkor lehet, ha x2=2x.
Erre jutottál Te is, csak a végén az a "más megoldás nincs" kijelentés nem elég meggyőző.
|
| Előzmény: [143] Iván88, 2006-01-20 22:16:57 |
|
|
| [142] lorantfy | 2006-01-19 22:37:54 |
 Szia Iván!
Megvizsgáltad az x2 és a 2x viszonyát x különböző értékeinél, most azt kéne megnézni, hogyan változik a log2(x2+2x) értéke ha x2 helyett 2x-t írsz bele! Közben a másik oldalon 2x helyett x2-t írunk!
Melyik intervallumon, hogyan változik a két oldal értéke?
|
| Előzmény: [139] Iván88, 2006-01-19 19:50:59 |
|
|
|
| [139] Iván88 | 2006-01-19 19:50:59 |
 Valaki monja meg, hogy hogyan kell megoldani(teljesen) a B. 3859-est!
Addig is elküldöm a B. 3871-esre az én megoldásomat.
B. 3871. Oldjuk meg az
x2-x-1=2x-log2(x2+2x)
egyenletet a pozitív számok körében.
Itt aztán minden van. Hatványtag, exponenciális tag és logaritmikus tag is. Nem éri meg kibontani őket. Néhány számot próbáljunk ki, hátha lesz valami. Így kapjuk azt hogy a 2 és a 4 megoldásai az egyenletnek. Megmutatjuk, hogy más megoldás nincsen.
Az én ötletem az volt, hogy (mivel az x2+2x szerepel a logaritmus után és az egyenlet mindkét oldalán (egyiken az egyyik, másikon a másik)) hasonlítrsuk össze az x2-et a 2x-nel. A két függvényt ábrázolva azt kapjuk, hogy x2=2x, ha x1;2=2; 4; x·2>2x, ha 2<x<4 , minden egyéb esetben 2x>x2, mivel 0<x.
Nézzük meg, hogy milyen relációkapcsolatban van x+1, a log2(x2+2x)-nel. Néhány ekvivalens átrendezés után azt kapjuk, hogy az x+1-ből 2x, a log2(x2+2x)-ből az x2-es tag "keletkezik".
Az eredeti egyenletet az alábbi alakra hozva azt kapjuk, hogy:
x2+log2(x2+2x)=2x+x+1
a bal oldalon állnak az "x2-es tagok" (reláció szempontjából), míg a jobb oldalon a "2x-esek". Mivel x2=2x, ha x1;2=2; 4, így más megoldás nincs.
|
|
| [138] Káli gúla | 2006-01-18 15:25:07 |
 B. 3867. Legyen az n olyan pozitív egész szám, amelyre 4n+2n+1 prímszám. Bizonyítsuk be, hogy n a 3-nak egész kitevőjű hatványa.
Ha n nem 3 hatvány, akkor van olyan p prímosztója, ami nem 3. Legyen n1=n/p és a=2n1. Ekkor a kérdezett szám N=a2p+ap+1. Azt fogjuk belátni, hogy N osztható (a2+a+1)-gyel. Ha a számot a alapú számrendszerben írjuk fel, akkor három egyes számjegye van --jobbról balra olvasva--, a nulladik, a p-edik és a 2p-edik, az összes többi jegye 0.
Tízes számrendszerben egy ilyen szám 999-cel osztva 111-et ad maradékul , mert a jegyeket jobbról balra hármasával csoportosítva a 999-es osztási maradékot ezeknek az ezres csoportoknak az összege adja, ami éppen 111 lesz, hiszen az egyesek helyén álló 1-es a csoportjában a jobb szélre kerül, a középső és a legnagyobb helyiértékű 1-es pedig a csoportjában biztosan a másik két pozícióra kerül (mivel p és 2p különbözőek és nem nullák mod 3).
Ugyanezt 10 helyett a-ra elmondva azt kapjuk, hogy N az (a3-1)-gyel osztva (a2+a+1)-et ad maradékul, amivel kész is vagyunk, hiszen (a2+a+1) | (a3-1), és persze a talált osztó 1<a2+a+1<N miatt valódi.
|
|
| [137] lorantfy | 2006-01-17 21:52:50 |
 Kedves Fórumosok!
Nekem az előző havi B feladatsorból ez a példa tetszett a legjobban. Köszönet érte Bodnár Jásnosnak, aki javasolta.
B.3869. megoldása: Azt fogjuk belátni, hogy LM párhuzamos BC oldallal. Ebből következik, hogy MN is párhuzamos BC-vel (hiszen ugyanúgy látható be) és így LN is az.
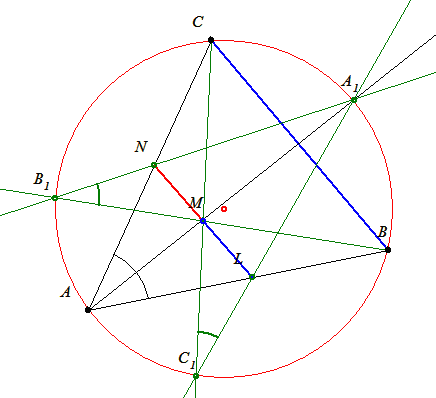
Egyszerűsítsük le a feladatot. Foglalkozzunk a BA1 és A1C egyenlő íveken nyugvó A és C1 csúcsú, egyenlő nagyságú kerületi kerületi szögekkel. Ezek szárai az L, M és P pontokban metszik egymást.
APM és C1PL háromszögeknek két-két szöge egyenlő, így az M és L csúcsoknál lévő szögek is egyenlőek. Tehát ezek a szögek az AC1 szakasz fölé emelt, azonos látókörívre esnek. (Vagyis AC1LM húrnégyszög.)
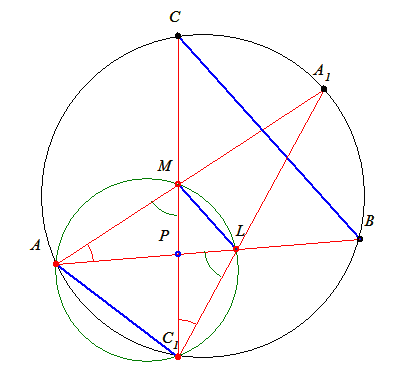
Ebben a körben C1AL és C1ML és C1ML a C1L ivhez tartozó kerületi szögek, tehát egyenlőek. AC1M a C1L ivhez tartozó kerületi szögek, tehát egyenlőek. AC1M és ALM és ALM az AM ívhez tartoz kerületi szögek tehát egyenlőek. Ebből már következik, hogy AC1P és LMP háromszögek hasonlóak, mert két szögük egyenlő. az AM ívhez tartoz kerületi szögek tehát egyenlőek. Ebből már következik, hogy AC1P és LMP háromszögek hasonlóak, mert két szögük egyenlő.
Ugyanigy belátható a nagyobb körben, hogy AC1P és BCP háromszögek hasonlóak. Ebből már következik, hogy LMP és BCP háromszögek is hasonlóak. Mivel ezen háromszögek P csúcsban lévő szöge közös, másik két szögük egyenlő, így LM párhuzamos BC oldallal.
|
|
|
| [135] nadorp | 2006-01-11 08:32:32 |
 Még nem,de majdnem. Tehát legyen a1=1 és ak=k.(k-1)-1, ha 2 k k p-1. Ez jónak tűnik, mert a1...ak p-1. Ez jónak tűnik, mert a1...ak k mod(p),hiszen k kivételével mindegyik tag inverze is szerepel a szorzatban. Már csak annak a bizonyítása van hátra, hogy ezek a számok különböző maradékot adnak p-vel osztva. Ehhez azt kell belátni, hogy egyrészt az 1 maradék csak egyszer fordul elő, másrészt, hogy az n.(n-1)-1 k mod(p),hiszen k kivételével mindegyik tag inverze is szerepel a szorzatban. Már csak annak a bizonyítása van hátra, hogy ezek a számok különböző maradékot adnak p-vel osztva. Ehhez azt kell belátni, hogy egyrészt az 1 maradék csak egyszer fordul elő, másrészt, hogy az n.(n-1)-1 k.(k-1)-1 mod(p) (2 k.(k-1)-1 mod(p) (2 n,k n,k p-1) kongruenciának csak n=k a megoldása. ( az esetszétválasztás azért kell, mert 0-nak nincs inverze). p-1) kongruenciának csak n=k a megoldása. ( az esetszétválasztás azért kell, mert 0-nak nincs inverze).
|
| Előzmény: [134] Iván88, 2006-01-10 20:26:18 |
|
|
| [133] nadorp | 2006-01-09 08:43:04 |
 Induljunk ki a Te megoldásodból.Ebben 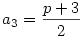 .Ekkor .Ekkor
2a3=p+3,azaz
2a3 3 mod(p). 3 mod(p).
Ha most a 2 inverzét ( lásd 125. hozzászólás) jelöli 2-1, akkor
a3 3.2-1 mod(p). Ez egy "szebb" alak,mert általánosítható. Legyen 3.2-1 mod(p). Ez egy "szebb" alak,mert általánosítható. Legyen
a1=1 a2=2.1 a3=3.2-1 a4=4x... Mi az x ? Folytasd a sorozatot.
|
| Előzmény: [132] Iván88, 2006-01-08 16:55:16 |
|
|
| [131] nadorp | 2005-12-30 20:38:32 |
 Ígéretes elindulás. Általában is igaz, hogy megválasztható a sorrend úgy, hogy a1a2...ak p-vel osztva k-t ad maradékul. Ehhez a konstrukcióhoz minden információ a rendelkezésedre áll a korábbi hozzászólások alapján.
|
| Előzmény: [130] Iván88, 2005-12-30 18:29:22 |
|
| [130] Iván88 | 2005-12-30 18:29:22 |
 Egy kicsit kanyarodjunk vissza a B. 3859-re. Az már volágos, hogy (p-1)!+1 osztható p-vel. Ha a sejtésem igaz, akkor a2=2 és a3=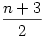 , egyellőre kifogytam az ötletekből, de hátha halakit ez elindít(ott). , egyellőre kifogytam az ötletekből, de hátha halakit ez elindít(ott).
|
| Előzmény: [121] Iván88, 2005-12-24 23:14:03 |
|
| [129] Geg | 2005-12-29 14:59:25 |
 A feladatot en javitottam, volt nehany ember, aki hasonloan igyekezett megkozeliteni a feladatot, de csak 1 vagy 2 volt az aki tisztessegesen vegigszamolta geometriaval az egeszet.
Lenyegesen egyszerubb megoldas ha vektorokat hasznalunk: fel kell irni a mozgasegyenletet tetszoleges testnek ugy, hogy az origo a tkp (hiszen nyilvan ekorul forog a rendszer ha a testek egymastol mert tavolsaga idoben allando), ekkor nehany egyszeru atalakitas soran kijon a szogsebesseg es az, hogy az nem fugg az eppen aktualis test tomegetol, csak az ossztomegtol.
|
| Előzmény: [126] lorantfy, 2005-12-28 23:12:10 |
|
| [128] lorantfy | 2005-12-29 11:14:31 |
 Szia Viktor!
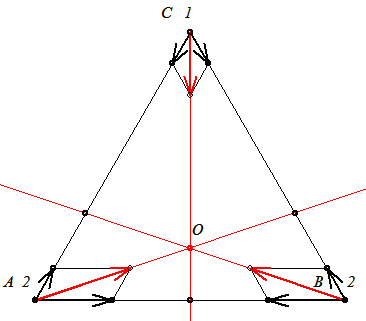
A szöveg azt mondja, hogy "bármely kettő közötti távolság megegyezik". Ez a te példád esetében csak úgy lehetne, ha az első két tömegpont egyenlő, a 3. pedig az őket összekötő szakasz felező merőlegesén van úgy, hogy egyenlő oldalú  -t alkossanak. A forgáspont akkor sem lehet az első kettő tömegközéppontjában, mert a grav. erők eredőinek hatásvonalai nem ott metszik egymást. -t alkossanak. A forgáspont akkor sem lehet az első kettő tömegközéppontjában, mert a grav. erők eredőinek hatásvonalai nem ott metszik egymást.
|
 |
| Előzmény: [127] xviktor, 2005-12-29 01:01:02 |
|
| [127] xviktor | 2005-12-29 01:01:02 |
 Olyan is lehet-e a rendszer, hogy 2 forog egy pont korul atellenben, a 3. meg a ketto sulypontja korul, a masik kettot osszekoto szakaszra meroleges sugarral?
Udv: Viktor
|
| Előzmény: [126] lorantfy, 2005-12-28 23:12:10 |
|
| [126] lorantfy | 2005-12-28 23:12:10 |
 Szia X!
P. 3833. Mozoghat-e három különböző tömegű pontszerű test egymás gravitációs terében úgy, hogy bármely kettő közötti távolság megegyezik és a mozgás során állandó marad? Mekkora szögsebességgel forog ez a rendszer?
A második kérdés sugallja a választ az elsőre. Forgatni kell a rendszert, méghozzá úgy, hogy a testekre ható gravitációs erők eredője éppen a körmozgást biztosító centripetális erő legyen.
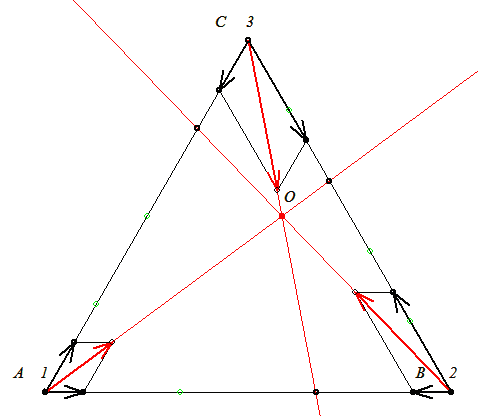
A testek egy egyenlő oldalú háromszög csúcspontjaiban vannak. Először keressül meg a forgás középpontját.
A testekre ható grav. erők eredőit meghosszabbítva ezek egy pontban metszik egymást, (ugyanis vektori eredőjük nulla, hiszen a komponensek összege is nulla) csak ez a pont lehet a forgás középpontja.
Fcp=mr 2, így azt kell még belátnunk, hogy ha OA=r1, OB=r2,OC=r3, akkor 2, így azt kell még belátnunk, hogy ha OA=r1, OB=r2,OC=r3, akkor
m1r1 : m2r2 : m3r3 = F1 : F2 : F3
Ezt belátni egy matematikai feladat, remélhetőleg sin-cos tételekkel menni fog!
|
 |
| Előzmény: [123] !X!, 2005-12-27 09:48:16 |
|
| [125] nadorp | 2005-12-28 16:00:33 |
 Azt bizonyították be, hogy a p(x) polinom az x=1,2,...,p-1 helyeken osztható p-vel, azaz ezek a számok a polinom gyökei modulo (p). Viszont ha egy test feletti (p-2)-ed fokú polinomnak (p-1) darab gyöke van, akkor az csak a 0 polinom lehet. Ha ez a bizonyítás nem tetszett, akkor itt egy másik.
Legyen x egy p-nél kisebb pozitív egész és tekintsük a x,2x,3x,...,(p-1)x számokat. Ezek a számok nem oszthatók p-vel és bármely kettő különböző maradékot ad p-vel osztva. Ezért van pontosan egy olyan y, hogy az xy p-vel osztva 1-et ad maradékul. Ezt az y-t a x multiplikatív inverzének nevezzük modulo p. Az is látszik, hogy csak az 1 és a p-1 önmaga inverze ( ha p|x2-1, akkor p|x-1 vagy p|x+1). Az előbbiek szerint a 2,3,...p-2 számok párba állíthatók úgy, hogy a két szám szorzata 1-t ad maradékul p-vel osztva. Ebből viszont az következik, hogy
2.3.....(p-2)=(p-2)! is 1-t ad maradékul mod (p).
|
| Előzmény: [124] Iván88, 2005-12-27 18:57:36 |
|
|
| [123] !X! | 2005-12-27 09:48:16 |
 A P.3833.-as feladatra senki nem tud valami okosat mondani?
|
|
| [122] Csimby | 2005-12-24 23:46:27 |
 Wilson-tétel:
Biz. vázlat:
p(x)=xp-1-1-(x-1)(x-2)...(x-(p-1))
p(x)-ben az első tag Kis-Fermat tétel szerint 1 maradékot ad p-vel osztva (ha x nem osztható p-vel), ugyanakkor az utolsó tag (a p-1 tényezős szorzat p-1 helyen is 0 maradékot ad p-vel osztva). Tehát p(x)-nek van legalább p-1 inkongruens gyöke. De p(x) foka p-2, hiszen a főtag kiesik. Ekkor a fokszámtétel szerint (Zp test) p(x)=0-nak legfeljebb p-2 inkongruens megoldása van. Ez ellentmondás, csak az oldja fel, ha p(x) a 0 polinom, vagyis minden együtthatója, így a0 is 0. Viszont a0=-1-(-1)p(p-1)! 0. Ha p>2 akkor p páratlan, tehát ezt kapjuk: -1 0. Ha p>2 akkor p páratlan, tehát ezt kapjuk: -1 (p-1)! Ami pont az általad megfogalmazott "sejtés". (p-1)! Ami pont az általad megfogalmazott "sejtés".
|
| Előzmény: [121] Iván88, 2005-12-24 23:14:03 |
|
| [121] Iván88 | 2005-12-24 23:14:03 |
 Sziasztok! Elakadtam a B. 3859-es feladattal. Leírom hol: Az biztos, hogy a1=1, különben két egymást követő érték azonos lesz 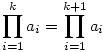 , ami ellentmond a feladat állításának (1<k<n). Igaz az is, hogy an=n, különben biztosan lesz legalább 2 szorzat, ami n-nel osztható, és ez sem lehet. Na mármost csak olyan n-ekre teljesülhet, ahol (n-1)!=xn NEM teljesül. (x pozitív egész) Iyenek kivétel nélkül a prímszámok, és az 1, meg a 4. Amit nem sikerült tisztáznom: Igaz e, hogy mindem n prímszámra teljesül? az első néhány prímre kipróbáltam, és azt sejtem, hogy igen, mindegyik prímre jó, méghozzá úgy, hogy , ami ellentmond a feladat állításának (1<k<n). Igaz az is, hogy an=n, különben biztosan lesz legalább 2 szorzat, ami n-nel osztható, és ez sem lehet. Na mármost csak olyan n-ekre teljesülhet, ahol (n-1)!=xn NEM teljesül. (x pozitív egész) Iyenek kivétel nélkül a prímszámok, és az 1, meg a 4. Amit nem sikerült tisztáznom: Igaz e, hogy mindem n prímszámra teljesül? az első néhány prímre kipróbáltam, és azt sejtem, hogy igen, mindegyik prímre jó, méghozzá úgy, hogy  n-nel osztva h maradékot ad (0<=h<n, egész). Igaz e? Ehhez egy segédlemma: Mivel n-nel osztva h maradékot ad (0<=h<n, egész). Igaz e? Ehhez egy segédlemma: Mivel  =(n-1)!, ezért Úgy sejtem, hogy tetszőleges p prímre (p-1)!+1 p-nek egész számú többszöröse (ez ekvivalens azzal, hogy =(p-2)!-1 p-nek az egész számú többszöröse), de ezt se tudom igazolni. Talán valaki ezek után már tudja folytatni. =(n-1)!, ezért Úgy sejtem, hogy tetszőleges p prímre (p-1)!+1 p-nek egész számú többszöröse (ez ekvivalens azzal, hogy =(p-2)!-1 p-nek az egész számú többszöröse), de ezt se tudom igazolni. Talán valaki ezek után már tudja folytatni.
|
|






 hasonló AB2C2
hasonló AB2C2 c1 és b2=
c1 és b2= =
= +
+ =B1AB2
=B1AB2 AC1C2
AC1C2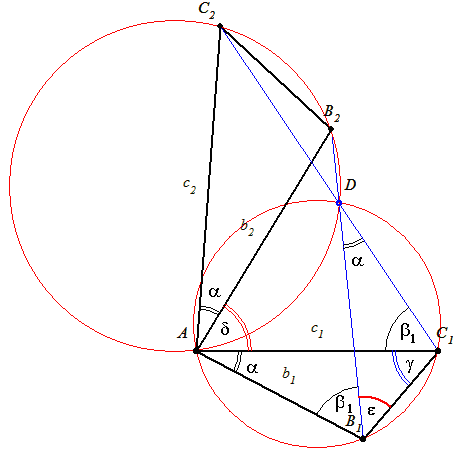
 1=AC1C2
1=AC1C2 és
és  mindkettőben közös, így B1DC1
mindkettőben közös, így B1DC1



 k
k k mod(p),hiszen k kivételével mindegyik tag inverze is szerepel a szorzatban. Már csak annak a bizonyítása van hátra, hogy ezek a számok különböző maradékot adnak p-vel osztva. Ehhez azt kell belátni, hogy egyrészt az 1 maradék csak egyszer fordul elő, másrészt, hogy az n.(n-1)-1
k mod(p),hiszen k kivételével mindegyik tag inverze is szerepel a szorzatban. Már csak annak a bizonyítása van hátra, hogy ezek a számok különböző maradékot adnak p-vel osztva. Ehhez azt kell belátni, hogy egyrészt az 1 maradék csak egyszer fordul elő, másrészt, hogy az n.(n-1)-1
 2, így azt kell még belátnunk, hogy ha OA=r1, OB=r2,OC=r3, akkor
2, így azt kell még belátnunk, hogy ha OA=r1, OB=r2,OC=r3, akkor 
