| [330] Willy | 2007-07-22 23:02:26 |
 P.3992-es feladat megoldása (***** ******* dolgozata alapján):
Legyen az elválás pillanatában a kistesthez húzott sugár és a függőleges által bezárt szög:  . Az elváláskor a félgömb már nem fejt ki erőt a kistestre és a kistest se a félgömbre, ezért egyik test sem fog gyorsulni, tehát inerciarendszereket alkalmazhatunk a feírásnál. Írjuk fel a következő egyenletet a kistest mozgására, a félgömbhöz rögzített rendszerben: . Az elváláskor a félgömb már nem fejt ki erőt a kistestre és a kistest se a félgömbre, ezért egyik test sem fog gyorsulni, tehát inerciarendszereket alkalmazhatunk a feírásnál. Írjuk fel a következő egyenletet a kistest mozgására, a félgömbhöz rögzített rendszerben:
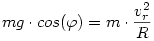 | (1) |
(vr nyilván a kistest, félgömbhöz viszonyított sebessége) Külső inerciarendszerből nézve, legyen a kistest vízszintes irányú sebessége vx, függőleges irányú vy illetve legyen a félgömb sebessége V. Írjuk fel ezeket a sebességeket a szögfüggvényekkel, a másik rendszer vr-jét felhasználva:
vr.cos( )=vx+V )=vx+V | (2) |
vr.sin( )=vy )=vy | (3) |
Továbbá belátható, hogy vízszintes irányban végig érvényes a lendület megmaradása az egész rendszerre nézve, tehát:
Továbbá, természetesen az energiamegmaradás is érvényesül:
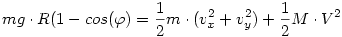 | (5) |
Most már minden egyenlet meg van; (2)-t, (3)-at, (4)-et és az (5)-t felhasználva a kistestnek vr-sebessége:
 | (6) |
(6)-t beírva a még nem használt (1)-be egy harmad fokú trigonometrikus egyenletet kapunk (és most lényeg, hogy ne sima polinomnak tekintsük):
 | (7) |
Most végezzük el a következő helyettesítéseket:
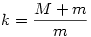 és és 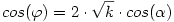 és osszunk és osszunk 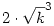 szorzattal; ekkor kapjuk a következőt: szorzattal; ekkor kapjuk a következőt:
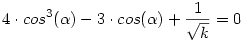
Használjuk fel a következő trigonometrikus azonosságot: 4.cos3( )-3.cos( )-3.cos( )=cos(3 )=cos(3 ), ami segítségével: ), ami segítségével:
![cos(\alpha)=cos\bigg[\frac13\cdot arccos\bigg(-\frac{1}{\sqrt k}\bigg)\bigg]](keplet.cgi?k=19D87D12CC2D781D) | (8) |
Most fejezzük ki az egyes sebességeket (1)-el, (2)-el, (3)-el és (4)-el:
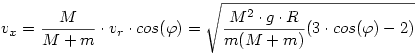 | (9) |
 | (10) |
Végül az a) részfeladatban keresett sebesség:
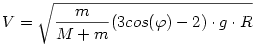 | (11) |
A különböző feladatrészekben a cos( )-t és a sin( )-t és a sin( )-t ismertnek tekintjük. )-t ismertnek tekintjük.
Miután elválik a félgömbtől a kistestegy parabola pályán mozog tovább, ferde hajytást szenved. Ennek sebességparaméterei ismertek, a helye számítható. Ezek alapján a ferde hajítás ideje legyen t:
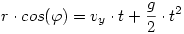 | (12) |
Természetesen a hajítás során vx nem változik, így a t idő alatt megtett út:
(12)-ből t valósnal tekinthető értékét kifejezve és (13)-ba beírva, felhasználva (9)-t és (10)-t:
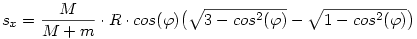 | (14) |
Az elválásig a kistest eleve megtett már valamekkora utat vízszintesen is (a koordináterendszer origóját a kiindulási helyzetben a testek tkp-jai alatt rögzítettük az asztall síkjában). Ezt könnyű meghatározni, mivel a rendszerre ható külső erők x irányú eredője minden pillanatban zérus, ezért a tömegközéppont csak x irányban helyben marad. Ezt, az elválásig az x irányban megtett utat jelöljük se-vel, ami a tömegközéppont értelmezése alapján:
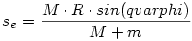
Ezek alapján a becsapódás pillanatában a kistest az:
![s=s_e+s_x=\frac{M\cdot R}{M+m}\Big[cos(\varphi)\big(\sqrt{3-cos^2(\varphi)}-\sqrt{1-cos^2(\varphi)}\big)+\sqrt{1-cos^2(\varphi)}\Big]](keplet.cgi?k=B3DEDB780E65DBA0)
Utat tette meg, felhasználva persze a (14)-es eredményt. A kistest függőleges irányú sebessége az asztalra való érkezéskor:
Mivel a vízszintes irányú sebesség nem változott, ezért a kistest sebessége a becsapódáskor:
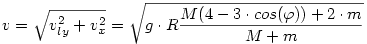
És iránytangense:
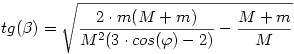
|
| Előzmény: [325] Alma, 2007-07-20 20:21:07 |
|
| [329] rizsesz | 2007-07-22 22:53:37 |
 Sajnos érdemes megnézni, hogy a megoldónál ez nem egyedi eset. És nem a moderátor mondja azt, hogy ez nem versenyszerű. Mint ahogyan a többi példára beküldött megoldásai esetében sem erről van szó. Hanem arról, hogy ő teszi fel a kérdést a honlapokon, hogy megválaszolják. És ha még töredéke is a megoldásnak a honlapon látott, akkor sem lehet azt mondani, hogy az illető nem vett igénybe külső segítséget.
|
| Előzmény: [328] Willy, 2007-07-22 18:09:10 |
|
| [328] Willy | 2007-07-22 18:09:10 |
 ÖÖÖ, hát, mit is mondjak... ez a link elég sovány ahhoz, hogy NVSZ-t adj neki, ha egyáltalán van jogod hozzá, mert nálam van a dolgozata és én javítom.
A link meg azért sovány, mert gyakorlatilag alig van köze a feladathoz (annak butított verzíója), neki pedig egy (ha ritkán is, de) észrevehető helyettesítéssel kicsikart megoldása volt, ami teljesen korrekt.
Egyáltalán ki vagy te/maga???
|
| Előzmény: [327] terminátor, 2007-07-22 17:05:21 |
|
|
| [326] Willy | 2007-07-22 00:14:00 |
 Persze, felteszem a helyes megoldást beküldő dolgozatát (holnap, asszem), de én nem értem, hogy a kedves ***** ******* dolgozata mi a túróért nem versenyszerű!? Mert én 5 pontot adtam neki, ergo (holnap) megy mégegy levél a szerknek, mert itt én valamit nagyon nem értek... vagy nem stimmel valami...
|
| Előzmény: [325] Alma, 2007-07-20 20:21:07 |
|
| [325] Alma | 2007-07-20 20:21:07 |
 Kedves Willy! Fel tudnad tenni a feladatnak a hivatalos megoldasat? Lattam nem lett 5 pontos :)...vicces...Iza sokat szenvedhetett a 4 pontert.
|
| Előzmény: [323] Willy, 2007-06-24 00:56:00 |
|
|
| [323] Willy | 2007-06-24 00:56:00 |
 Úgy nézem, kelleni is fog... én is belebotlottam abba a harmad fokú egyenletbe (körpályán való mozgásból, az energia- és a lendületmegmaradásból), nekem ez jött ki, a teljesség igénye nélkül (remélem nem rontottam el), a végleges megfejtést majd kiírom:
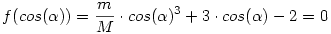
Ugye ezt cos( )-ra kéne megoldani, én a Newton módszert használtam, egyetlen lépéssel, amiból a zérushelyre, ha megfelelő xo-t választunk, akkor elég pontosan: )-ra kéne megoldani, én a Newton módszert használtam, egyetlen lépéssel, amiból a zérushelyre, ha megfelelő xo-t választunk, akkor elég pontosan:
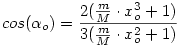
Hát... "ránézésre" xo-nak olyan 2/3-ot érdemes választani, de megnéztem géppel, nagy (8-10 körüli) m/M esetén a 0,5-ös kezdőérték még kedvezőbb...
Én úgy egyszerűsíteném tovább, hogy az  értékére értékére 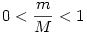 esetén két közelítő, de állandó értékkel folytatnám... jobb híján... (ezek lehetnek cos( esetén két közelítő, de állandó értékkel folytatnám... jobb híján... (ezek lehetnek cos( 1)=0,66 és cos( 1)=0,66 és cos( 2)=0,60) amikből már lehet számolni helyeket, egy tartományt, ahol becsapódhat meg minden mást... meg paraméteresen is megadható. Ti mit gondoltok? 2)=0,60) amikből már lehet számolni helyeket, egy tartományt, ahol becsapódhat meg minden mást... meg paraméteresen is megadható. Ti mit gondoltok?
Ami engem érdekel, az a "hívatalos" megoldás... lehet, hogy tényleg van egyszerűbb megoldása a problémának... konkrét értékekkel persze könnyebb lenne.
Kérdésedre a válasz: annyit tudok, hogy a munkafüzetbe csak ketten küldtek megoldást.
|
| Előzmény: [322] Alma, 2007-06-23 22:10:58 |
|
|
| [321] Willy | 2007-06-23 14:43:24 |
 Helló Alma és Dani!
Úgy esett, hogy én javítom a P.3992-est, vagy mit... jól belenyúltam.
Ha ti ketten együtt nem találtatok triviális megoldást, akkor szerintem én sem fogok összehozni semmit, majd, ha megnézem... Viszont majd megkérdezem a megoldást (ha már belefáradtam az egészbe), azt majd felteszem ide.
A pontozást majd meglátom...
|
| Előzmény: [309] Alma, 2007-06-12 21:59:48 |
|
|
| [319] Gyöngyő | 2007-06-18 19:09:18 |
 Még annyit,hogy hol találtad meg?
Köszönettel:
Gyöngyő
|
|
| [318] Gyöngyő | 2007-06-18 19:06:31 |
 Köszönöm szépen!!!
Üdv.: Gyöngyő
|
|
|
| [316] Gyöngyő | 2007-06-18 14:05:54 |
 Sziasztok!
Már régebben is írtam,de akkor nem kaptam választ az A.414 es feladat megoldására! Tudnátok esetleg segíteni?
Üdv.: Gyöngyő
|
|
| [315] Vonka Vilmos Úr | 2007-06-16 18:23:17 |
 Olyan pont, amire a kapott kúpszelet kör lesz, pontosan egy lesz a síkban; hiszen a kúpszelet áthalad az A, B, C pontokon, tehát nem lehet más, mint a háromszög körülírt köre. Ezt a pontot úgy lehet megtalálni, hogy a körülírt kör tetszőleges P és P' pontjából "visszaszerkesztjük" a hozzájuk tartozó B' és C' pontokat, és a B'C' egyenes így megkapott két helyzetének metszéspontja adja a keresett A' pontot. Azt pedig, hogy a B'C' egyenes különböző helyzetei sugársort alkotnak, azzal igazolhatjuk, hogy ha éppen a P=A pontból indulunk ki, akkor mind a B', mind a C' pont az A pontba kerül, tehát a (B') és (C') pontsorok valóban perspektív helyzetűek.
|
| Előzmény: [312] Yegreg, 2007-06-16 15:15:38 |
|
| [314] Vonka Vilmos Úr | 2007-06-16 17:41:24 |
 A (B') pontokból álló AC tartóegyenesű és a (C') pontokból álló AB tartóegyenesű pontsorok az A' középponttal perspektív helyzetűek. Így B-ből vetítve a (B') pontokat és C-ből vetítve a (C') pontokat egymáshoz projektív sugársorokat kapunk. P éppen a projektivitásban egymásnak megfelelő egyenesek metszéspontja. Projektív sugársorok metszési alakzatáról pedig jól ismert (Steiner-tétel), hogy kúpszelet. Ezen kúpszeletre illeszkednek a sugársorok tartópontjai (B és C). A (B') és (C') pontsorok perspektivitásában az A pont fix, így a BA és CA egyenesek a projektivitásban egymásnak felelnek meg, tehát az A pont is illeszkedik a fenti kúpszeletre.
|
| Előzmény: [310] Yegreg, 2007-06-16 14:31:25 |
|
| [313] Anum | 2007-06-16 16:49:54 |
 Hát igen. Nekem is hasonló. Progi nélkül nem jött ki. Így nem is vesződtem vele. Két lehetőséget látok:
1. vagy van valami nagyon "frappáns" megoldás. 2. a versenyzők türelmét, számolási késégét kívánták mérni,
Ha 1. akkor várjuk a választ! :)
Ha 2. akkor ezt a feladatot inkább valmely matek pontversenybe kellett volna kitűzni. Nem látom sok értelmét egy viszonylag kevés (mondhatni minimális) fizikai tartalommal rendelkező ám annál magasabb matematikai ismereteket megkövetelő feladat kitűzésének.
Remélem az 1. áll fenn, mert a 2. elég kiábrándító lenne...
|
| Előzmény: [307] Alma, 2007-06-12 13:41:56 |
|
| [312] Yegreg | 2007-06-16 15:15:38 |
 És akkor felmerül a kérdés, hogy egy általános ABC háromszög esetén mely pontokra lesz a kapott kúpszelet kör?
|
|
| [311] Yegreg | 2007-06-16 15:13:47 |
 Persze, ebből az is következik, hogy ha ABC nem szabályos, akkor is igaz az állítás.
|
|
| [310] Yegreg | 2007-06-16 14:31:25 |
 B4004. módosítása:
Adott az ABC szabályos háromszög síkjában egy A' pont. Egy, az A'-n átmenő egyenes az AB és AC egyeneseket rendre a C' és a B' pontokban metszi (az egyszerűség kedvéért B' és C' lehetnek ideális pontok is). Igazoljuk, hogy a BB' és a CC' egyenesek metszéspontjának mértani helye egy, az A, B és C pontokon átmenő kúpszelet (ellipszis, hiperbola, parabola, kör vagy két metsző egyenes)!
|
|
|
| [308] tüzes | 2007-06-12 20:22:26 |
 Kedves Alma! (Re: P.3992) Megpróbáltam megoldani a példát kézzel, nem ment. Próbáltam számítógépes programmal, nem ment. A szögre én is kaptam harmadfokú egyenletet, melyből én két nem valós és 1 valós gyököt kaptam. (Azért nem valós, mert volt benne i, és a program sehogy sem tudta kiküszöbölni). A páldában kitűzött kérdésekre csak program által adott eredményekkel tudtam válaszolni, de a becsapódás helyét még a számítógép sem tudta kiszámolni (egzakt módon). Akinek sikerült megoldania bármilyen módszerrel, kérjük ossza meg velünk eredményét!
|
| Előzmény: [307] Alma, 2007-06-12 13:41:56 |
|
| [307] Alma | 2007-06-12 13:41:56 |
 A mostani számban volt egy fizikafeladat, a P.3992., ami nekem nem nagyon tetszett. Én az elválási szög koszinuszára egy szép paraméteres harmadfokú egyenletet kaptam, aminek természetesen 3 valós gyöke van (és i-t egyikből sem tudtam kiküszöbölni). Mi nyílván csak a 0 és 1 közé esőt keressük. Ebből kellett még sebességet, becsapódási sebességet és még földetérés helyét is számolni. Szerintem ez csak papírral és ceruzával közel lehetetlen (rengeteg munka és hogy melyik gyök van 0 és 1 között az nem is egyszerű) Úgy gondoltam, hogy +1 pont nekem nem ér meg ennyi fáradságot. Valaki megcsinálta a feladatot? Ha valaki tud frappáns megoldást (program használata NÉLKÜL), annak nagyon örülnék ha megosztaná velem.
|
|
| [306] Gyarmati Péter | 2007-06-06 15:38:07 |
 A 2004. szeptemberi számban jelent meg a K.1. feladat. A tábla felállítás helytelen, mert a jobb alsó sarok (h1) színe világos kell, hogy legyen. Az utolsó soron (világos esetében a nyolcadikon) nem állhatnak gyalogok, mert ott át kell változniuk valamilyen tisztté.
Mit akartam ezzel mondani? Egy több ezer éves játék a kultúra része; figyeljünk rá jobban, még ha csak eszközként is használjuk, mint például a K.1-ben.
|
|



 . Az elváláskor a félgömb már nem fejt ki erőt a kistestre és a kistest se a félgömbre, ezért egyik test sem fog gyorsulni, tehát inerciarendszereket alkalmazhatunk a feírásnál. Írjuk fel a következő egyenletet a kistest mozgására, a félgömbhöz rögzített rendszerben:
. Az elváláskor a félgömb már nem fejt ki erőt a kistestre és a kistest se a félgömbre, ezért egyik test sem fog gyorsulni, tehát inerciarendszereket alkalmazhatunk a feírásnál. Írjuk fel a következő egyenletet a kistest mozgására, a félgömbhöz rögzített rendszerben:  )-3.cos(
)-3.cos(

 0 és xy(x2-y2)=x2+y2.
0 és xy(x2-y2)=x2+y2.  , y=rsin
, y=rsin  )
)  4 és egyenlőség sin 4
4 és egyenlőség sin 4




