| [345] öreg | 2007-08-07 12:06:35 |
 Nosztalgiából megnéztem a 2007. májusi feladatokat és megoldásokat és elszomorodtam, illetve megijedtem, hogy ennyire öregszem mert két megoldást nem értek.:(
A C.900. feladatnál már a kérdéssel is bajban voltam, mert kicsit magyartalan a megfogalmazás. De a megoldásból megértettem a kérdést. Viszont miért csak a (216;162) a megoldás? A (324;234)(432;324)(540;405)(648;486)(756;567)(864;648)(972;729) miért nem elégíti ki a feltételeket?
A B.4011.-es feladatnál pedig a kiírás szerint 2007 lakója van a falunak, a megoldás pedig mintha 103 lakosra lenne megadva.
Már nagyon rég volt, de szép emlék a KÖMAL...
|
|
| [344] rizsesz | 2007-07-31 01:18:13 |
 az én problémám nem ez volt, hanem az, hogy a feladat még nem volt hozzáférhető, se az újságban, sem a neten. ellenben az illető felrakta egy honlapra azt a feladatot április akárhányadikán, ami a kömalban május 10.-e után jelent meg.
|
|
| [343] Doom | 2007-07-25 09:48:48 |
 Szerintem nagyon is tudja... Csak van, akinek elég "érdekes" a fontossági és érték-sorrendje.
Viszont a kiszivárogtatás, főleg a rendszeres szerintem sem valós probléma. Ráadásul minél hamarabb rakja ki valaki a kérdést egy fórumra, annál nagyobb az esélye, hogy egy rivális is megtalálja. Sőt, így valószínűleg csak az eredeti kirakó dolgozata lesz NVSZ, így előbb-utóbb (a picit is nagyobb tömeg csinálja ezt) rá fognak döbbeni, hogy pont az első ember szívja meg és csak másoknak segít saját maga ellen, így talán ez elég elrettentésnek, ha amúgy is csak azért csinálta, hogy ő nyerjen.
|
| Előzmény: [342] Willy, 2007-07-25 01:53:51 |
|
| [342] Willy | 2007-07-25 01:53:51 |
 Hát, csak azt nem értem, hogy az aki csal miért nem érti, hogy ezzel leginkább önmagát csapja be...
Az, meg, hogy egy feladat hogyan szivárog ki, hát engem is nagyon érdekelne... de nem hinném, hogy erről volna szó. Az már nagyon durva lenne... kb. mint az, amit Jonas írt.
|
| Előzmény: [341] rizsesz, 2007-07-24 16:44:11 |
|
| [341] rizsesz | 2007-07-24 16:44:11 |
 Szerintem annak is érdemes lenne utánajárni, hogy hogyan szivároghatott ki idő előtt a feladat. Már ha erről van szó (a jóindulat szóljon belőlem: a feladat előkerült valamilyen válogatón, szakkörön, satöbbi)... azt mindenesetre ne mesélje be nekem senki, hogy 1 hónappal a feladat megjelenése előtt ő pont ezt a feladatot rakta ki egészen véletlenül 1 fórumra, hogy oldjátok meg...
|
|
| [340] Alma | 2007-07-24 15:58:46 |
 Szerintem aki egy pontverseny feladatát kitűzi fórumon határidő lejárta előtt és aztán a saját nevével beküldi azt, az szánalmas. Aki ezt más nevében teszi a kitűzést az nem csak szánalmas hanem aljas, rosszindulatú, bunkó, tirpák, gerinctelen és undorító is. Szerintem nincs olyan kömalozó aki ilyet tenne.
|
| Előzmény: [339] jonas, 2007-07-24 11:16:44 |
|
| [339] jonas | 2007-07-24 11:16:44 |
 A legrosszabb (és nem akarok ötleteket adni), hogy elvileg más valaki is beküldhet egy versenyző nevével nem versenyszerű dolgozatokat, vagy megkérdezheti látszólag a versenyző nevében a feladatot egy internetes fórumon. Ezt úgy is meg lehet tenni, hogy gyakorlatilag lehetetlen kinyomozni.
|
|
| [338] Willy | 2007-07-23 23:28:17 |
 Bocs, Rizsesz, szerintem kicsit elbeszélünk egymás mellett. Én (most már, hogy beszéltem Gézával) teljesen egyet értek mind Vele, mind Veled, mind a szerk.-el, teljesen igaza volt. Csak egy egyszerű félreértésről van itt szó, mert azt hittem, hogy a T100-as nem hivatalos személy és csak piszkálódik velem.
Az, hogy hogyan volt ez a linkes dolog, én már nem mondom... szerintem megegyezhetünk, hogy nem jövőlátásról, inkább egy félreértésről volt szó, de Gézával már beszéltünk erről, azt mondta gondolkoznak még rajta. Egy viszont biztos, hogy félreértés ne essék, a versenyző dolgozatát nem látták, nem a dolgozat alapján hozták meg a döntést, de ez Géza elmondása alapján mindegy is volt.
Ami a javítást illeti, szerintem ebben is mindannyian egyre gondolunk. Igazságosnak és precíznek kell lenni, max a módszerekben nem értünk egyet. Én pl. próbálnék aktívan visszajelezni a szerk.-nek, hátha hasznos javaslatokkal szolgálok (ki tudja), persze, nem csinálom ezt valami jól... (de a jószándék és az igazságérzet vezérelt).
A versenyzőkkel kapcsolatban meg... nem tudod elhinni, hogy én mennyire sajnálom, hogy egyesek ilyet csinálnak. Amikor még én versenyeztem, én azért csináltam, mert kihívást jelentett, meg gyakorolhattam. Kár, hogy ma egyeseknek csak a győzelem számít (persze hála az égnek a legtöbbeknél ez úgy van, mint nálam volt). Így belegondolva, tudod nekem milyen rossz érzés javítanom? Honnan tudjam mostantól, hogy az, akinek a dolgozatával meg voltam elégedve, tényleg megérdemelte-e (ha nem ismerem személyesen és nem tudom róla, hogy bizony ő olyat nem tenne)? Én is azt mondom, hogy el kell kapni őket, máskülönben javítani sem lesz olyan jó, mint 10 hónappal ezelőtt, naívan. De azt is mondom, hogy ez sem egyszerű...
|
| Előzmény: [337] rizsesz, 2007-07-23 21:59:43 |
|
| [337] rizsesz | 2007-07-23 21:59:43 |
 kedves Willy!
szerintem ezt tényleg meg kellene értened, hogy Géza mondatai mekkora igazságtartalommal bírnak ("A külső segítséggel kapcsolatban: erre szokták mondani, hogy az uszodában sokan belepisilnek a medencébe, de nem mindenki a trambulinról. Az, hogy sokan megússzák, nem jelentheti azt, hogy mindenkinek nézzük el.")
abba meg aztán végképp nem kívánok belegondolni, hogy mi lesz, ha ilyen jövőlátó versenyzők lepik el a pontversenyt, akik már áprilisban előre ismerik a májusi feladat számát... mert azért azt hiszem, ez is elég értelemzavaró.
és azt hiszem a javítók munkájáról annyit, hogy én nemrégiben újra javítottam egy feladatot, amit a javító édesapja javított ki.
zárszóként pedig szerintem tényleg érdemes a szerkesztőségnek azért alárendeltnek érezni magad. ahogyan nyilván ők sem az alapján adtak nvsz-t, hogy ezt a linket megnézték, hanem ők is megnézték a dolgozatot.
üdv, András
|
|
| [336] Willy | 2007-07-23 13:42:46 |
 Ok, elnézést a szófordulatokért, azt tényleg nem kellett volna feltétlenül betennem, de itt akkor is vannak bökkenők (szerintem). Persze ez nem igaz minden esetben, de szerintem mégis csak érdemes volna a javítónak is szólni, ha ilyen probléma van a dolgozatával kapcsolatban. Talán ő tényleg el tudja dönteni, hogy igaz-e a vád, vagy csak tévedés az. (Ez a vád, ebben az esetben, ha engem kérdeznek, egy hibás döntés volt, legalábbis engem nem tudott meggyőzni a link. Sem időbeli, sem logikai egyezést nem láttam a két dolog között. Persze ez még nem zár ki más csalást.)
Azt köszönöm, ha becsülitek a munkám, végülis ezért is szóltam be... meg nem szerettem volna balhét, hogy volt valami galiba, amiről javítóként nem is tudok. (Meg a rossz terészetem jellemzője, hogy nem szeretem, ha az ilyenből kihagynak, kicsit sért.)
Természetesen a szerkeztőség beleszólási jogát teljes mértékben tiszteletben tartom, nem erről van szó. A T100-ról nem tudtam, hogy ki ő, mit csinál(hat), mert ok, ő egy vicces figura, de nem tűnik formális személynek (mint pl. a Moderátor), aki a szerk.-nek dolgozik.
Ha itt a fórumon lehetséges, akkor pedig javasolnám a szerk.-nek, hogy ha lehetséges és nem okoz problémát az ilyen és hasonló problémákkal a javítót is keressék fel. Szerintem ez egy logikus lépés lenne ráadásul talán könnyebb és igazságosabb lenne az ítélkezés.
***
Arról, hogy egyesek nemzetközi fórumokon rákérdeznek a feladatokra én is hallottam, és nagyon sajnálom, hogy ez van. Félek, hogy ez a sportszerűtlenség, innentől egy állandó probléma lesz.
|
| Előzmény: [335] Kós Géza, 2007-07-23 12:54:31 |
|
| [335] Kós Géza | 2007-07-23 12:54:31 |
 A szerkesztőségnek jogában áll megváltoztatni a pontszámokat, ehhez nincs szükség sem a javító tájékoztatására, sem egyetértésére. Ha a javító nem érti, mi történt, akkor megkérdezheti egy udvarias e-mailben, persze szigorúan kerülve az olyan szófordulatokat, mint hogy "mi a túróért".
Btw a változtatás nem jelenti azt, hogy bárki is elégedetlen lenne a munkáddal; senki sem vonja kétségbe, hogy tisztességesen és pontosan dolgoztál.
* * *
Valaki több KöMaL feladatot megkérdezett internetes fórumokon, jóval a beküldési határidő előtt. Kb. 10 ilyen esetről tudunk, ezek többsége a mathlinksen jelent meg, de találtunk máshol is. Volt, amikor megmondták neki a megoldást, és be is küldte (ugyanazokkal a hiányosságokkal, mint ahogy megsúgták neki), olyan is volt, amikor nem súgták meg neki, és nem küldte be, és volt olyan is, amikor nem mondták meg, vagy hibás megoldásokat adtak, és nem azt küldte be.
Egy ilyen jelenség az egész pontversenyt súlyosan veszélyeztetheti. Képzeld el, amikor a mathlinks A-jelű feladatokban érdekelt magyar vendégei megtalálják az összes aktuális A-jelű feladatot. Még jó, hogy csak egyet oldottak meg neki.
A szerkesztőség hosszú vita után úgy döntött, hogy az illető versenyző minden olyan feladatra, amit a határidő előtt valamilyen nyilvános fórumon megkérdezett, majd beküldött, nvsz-t kap függetlenül attól, hogy mit küldött be, illetve kapott-e használható segítséget. Úgy gondolom, hogy a szóba jöhető szankciók közül ez a legenyhébb. Akkor sem szólhatna senki semmit, ha kizártuk volna a pontversenyből.
A dátumok alapján tényleg lehetséges, hogy a P.3992. esetében tévedtünk, ezt még nem késő felülvizsgálni.
* * *
A külső segítséggel kapcsolatban: erre szokták mondani, hogy az uszodában sokan belepisilnek a medencébe, de nem mindenki a trambulinról. Az, hogy sokan megússzák, nem jelentheti azt, hogy mindenkinek nézzük el.
Hasta la vista.
|
|
|
| [333] vogel | 2007-07-23 00:26:20 |
 A versenyző, aki a megoldást írta, nem fiú? :-D (itt a fórumon kisfox) Elnézést, hogy beleszólok, de a február az a joined dátum. Ez a hsz dátuma: Posted: Thu Apr 19, 2007 5:08 pm
|
|
|
| [331] Willy | 2007-07-22 23:18:31 |
 Nem arról van szó Rizsesz, a csajnak nem számít az, hogy megkapja-e a feladatra a pontokat vagy sem, nem lesz jobb a helyezése. Itt elvi kérdésekről van szó. Megnézed a megoldást, köze sincs a linken olvashatóhoz. Másrészt... miféle külső segítség? Hányszor van az, hogy a felkészítő tanár, vagy valami különtanár kicsit többet segít annál, mint amennyit illenék. Az még ráadásul ellenőrizhetetlenebb.
De ami a legjobban fájt, hogy valaki, akiről azt sem tudom, hogy ki NVSZ-t adott egy olyan feladatra, amelyet én javítok és amiért én felelek úgy, hogy még nem is láthatta, mivel még mindig nálam van a lány megoldása. Ráadásul meg sem kérdeztek, aminél nagyobb "csúnyaságot" el sem tudok képzelni. (Legalábbis Terminátor azt állítja, hogy ő volt.) Nomeg a feladat makulátlan és hibátlan. (Erre varrj gombot, mert én nem tudok.) Ha valaki, akárki úgy érzi, hogy egy másik valaki, akárki valami disznóságot csinált, akkor keresse meg a javítót e-mailen és azzal konzultáljon (én ezt így kérem). De ne a hátam mögött csinálják már, ha megkérhetném azt az akárkit.
OKÉ, T100???
|
| Előzmény: [329] rizsesz, 2007-07-22 22:53:37 |
|
| [330] Willy | 2007-07-22 23:02:26 |
 P.3992-es feladat megoldása (***** ******* dolgozata alapján):
Legyen az elválás pillanatában a kistesthez húzott sugár és a függőleges által bezárt szög:  . Az elváláskor a félgömb már nem fejt ki erőt a kistestre és a kistest se a félgömbre, ezért egyik test sem fog gyorsulni, tehát inerciarendszereket alkalmazhatunk a feírásnál. Írjuk fel a következő egyenletet a kistest mozgására, a félgömbhöz rögzített rendszerben: . Az elváláskor a félgömb már nem fejt ki erőt a kistestre és a kistest se a félgömbre, ezért egyik test sem fog gyorsulni, tehát inerciarendszereket alkalmazhatunk a feírásnál. Írjuk fel a következő egyenletet a kistest mozgására, a félgömbhöz rögzített rendszerben:
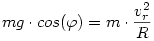 | (1) |
(vr nyilván a kistest, félgömbhöz viszonyított sebessége) Külső inerciarendszerből nézve, legyen a kistest vízszintes irányú sebessége vx, függőleges irányú vy illetve legyen a félgömb sebessége V. Írjuk fel ezeket a sebességeket a szögfüggvényekkel, a másik rendszer vr-jét felhasználva:
vr.cos( )=vx+V )=vx+V | (2) |
vr.sin( )=vy )=vy | (3) |
Továbbá belátható, hogy vízszintes irányban végig érvényes a lendület megmaradása az egész rendszerre nézve, tehát:
Továbbá, természetesen az energiamegmaradás is érvényesül:
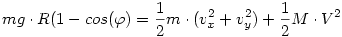 | (5) |
Most már minden egyenlet meg van; (2)-t, (3)-at, (4)-et és az (5)-t felhasználva a kistestnek vr-sebessége:
 | (6) |
(6)-t beírva a még nem használt (1)-be egy harmad fokú trigonometrikus egyenletet kapunk (és most lényeg, hogy ne sima polinomnak tekintsük):
 | (7) |
Most végezzük el a következő helyettesítéseket:
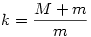 és és 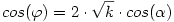 és osszunk és osszunk 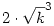 szorzattal; ekkor kapjuk a következőt: szorzattal; ekkor kapjuk a következőt:
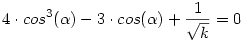
Használjuk fel a következő trigonometrikus azonosságot: 4.cos3( )-3.cos( )-3.cos( )=cos(3 )=cos(3 ), ami segítségével: ), ami segítségével:
![cos(\alpha)=cos\bigg[\frac13\cdot arccos\bigg(-\frac{1}{\sqrt k}\bigg)\bigg]](keplet.cgi?k=19D87D12CC2D781D) | (8) |
Most fejezzük ki az egyes sebességeket (1)-el, (2)-el, (3)-el és (4)-el:
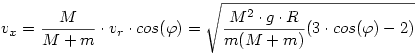 | (9) |
 | (10) |
Végül az a) részfeladatban keresett sebesség:
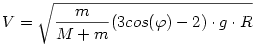 | (11) |
A különböző feladatrészekben a cos( )-t és a sin( )-t és a sin( )-t ismertnek tekintjük. )-t ismertnek tekintjük.
Miután elválik a félgömbtől a kistestegy parabola pályán mozog tovább, ferde hajytást szenved. Ennek sebességparaméterei ismertek, a helye számítható. Ezek alapján a ferde hajítás ideje legyen t:
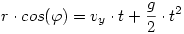 | (12) |
Természetesen a hajítás során vx nem változik, így a t idő alatt megtett út:
(12)-ből t valósnal tekinthető értékét kifejezve és (13)-ba beírva, felhasználva (9)-t és (10)-t:
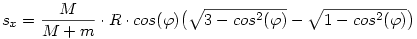 | (14) |
Az elválásig a kistest eleve megtett már valamekkora utat vízszintesen is (a koordináterendszer origóját a kiindulási helyzetben a testek tkp-jai alatt rögzítettük az asztall síkjában). Ezt könnyű meghatározni, mivel a rendszerre ható külső erők x irányú eredője minden pillanatban zérus, ezért a tömegközéppont csak x irányban helyben marad. Ezt, az elválásig az x irányban megtett utat jelöljük se-vel, ami a tömegközéppont értelmezése alapján:
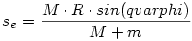
Ezek alapján a becsapódás pillanatában a kistest az:
![s=s_e+s_x=\frac{M\cdot R}{M+m}\Big[cos(\varphi)\big(\sqrt{3-cos^2(\varphi)}-\sqrt{1-cos^2(\varphi)}\big)+\sqrt{1-cos^2(\varphi)}\Big]](keplet.cgi?k=B3DEDB780E65DBA0)
Utat tette meg, felhasználva persze a (14)-es eredményt. A kistest függőleges irányú sebessége az asztalra való érkezéskor:
Mivel a vízszintes irányú sebesség nem változott, ezért a kistest sebessége a becsapódáskor:
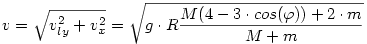
És iránytangense:
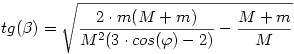
|
| Előzmény: [325] Alma, 2007-07-20 20:21:07 |
|
| [329] rizsesz | 2007-07-22 22:53:37 |
 Sajnos érdemes megnézni, hogy a megoldónál ez nem egyedi eset. És nem a moderátor mondja azt, hogy ez nem versenyszerű. Mint ahogyan a többi példára beküldött megoldásai esetében sem erről van szó. Hanem arról, hogy ő teszi fel a kérdést a honlapokon, hogy megválaszolják. És ha még töredéke is a megoldásnak a honlapon látott, akkor sem lehet azt mondani, hogy az illető nem vett igénybe külső segítséget.
|
| Előzmény: [328] Willy, 2007-07-22 18:09:10 |
|
| [328] Willy | 2007-07-22 18:09:10 |
 ÖÖÖ, hát, mit is mondjak... ez a link elég sovány ahhoz, hogy NVSZ-t adj neki, ha egyáltalán van jogod hozzá, mert nálam van a dolgozata és én javítom.
A link meg azért sovány, mert gyakorlatilag alig van köze a feladathoz (annak butított verzíója), neki pedig egy (ha ritkán is, de) észrevehető helyettesítéssel kicsikart megoldása volt, ami teljesen korrekt.
Egyáltalán ki vagy te/maga???
|
| Előzmény: [327] terminátor, 2007-07-22 17:05:21 |
|
|
| [326] Willy | 2007-07-22 00:14:00 |
 Persze, felteszem a helyes megoldást beküldő dolgozatát (holnap, asszem), de én nem értem, hogy a kedves ***** ******* dolgozata mi a túróért nem versenyszerű!? Mert én 5 pontot adtam neki, ergo (holnap) megy mégegy levél a szerknek, mert itt én valamit nagyon nem értek... vagy nem stimmel valami...
|
| Előzmény: [325] Alma, 2007-07-20 20:21:07 |
|
| [325] Alma | 2007-07-20 20:21:07 |
 Kedves Willy! Fel tudnad tenni a feladatnak a hivatalos megoldasat? Lattam nem lett 5 pontos :)...vicces...Iza sokat szenvedhetett a 4 pontert.
|
| Előzmény: [323] Willy, 2007-06-24 00:56:00 |
|
|
| [323] Willy | 2007-06-24 00:56:00 |
 Úgy nézem, kelleni is fog... én is belebotlottam abba a harmad fokú egyenletbe (körpályán való mozgásból, az energia- és a lendületmegmaradásból), nekem ez jött ki, a teljesség igénye nélkül (remélem nem rontottam el), a végleges megfejtést majd kiírom:
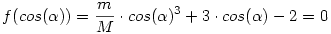
Ugye ezt cos( )-ra kéne megoldani, én a Newton módszert használtam, egyetlen lépéssel, amiból a zérushelyre, ha megfelelő xo-t választunk, akkor elég pontosan: )-ra kéne megoldani, én a Newton módszert használtam, egyetlen lépéssel, amiból a zérushelyre, ha megfelelő xo-t választunk, akkor elég pontosan:
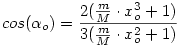
Hát... "ránézésre" xo-nak olyan 2/3-ot érdemes választani, de megnéztem géppel, nagy (8-10 körüli) m/M esetén a 0,5-ös kezdőérték még kedvezőbb...
Én úgy egyszerűsíteném tovább, hogy az  értékére értékére 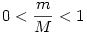 esetén két közelítő, de állandó értékkel folytatnám... jobb híján... (ezek lehetnek cos( esetén két közelítő, de állandó értékkel folytatnám... jobb híján... (ezek lehetnek cos( 1)=0,66 és cos( 1)=0,66 és cos( 2)=0,60) amikből már lehet számolni helyeket, egy tartományt, ahol becsapódhat meg minden mást... meg paraméteresen is megadható. Ti mit gondoltok? 2)=0,60) amikből már lehet számolni helyeket, egy tartományt, ahol becsapódhat meg minden mást... meg paraméteresen is megadható. Ti mit gondoltok?
Ami engem érdekel, az a "hívatalos" megoldás... lehet, hogy tényleg van egyszerűbb megoldása a problémának... konkrét értékekkel persze könnyebb lenne.
Kérdésedre a válasz: annyit tudok, hogy a munkafüzetbe csak ketten küldtek megoldást.
|
| Előzmény: [322] Alma, 2007-06-23 22:10:58 |
|
|
| [321] Willy | 2007-06-23 14:43:24 |
 Helló Alma és Dani!
Úgy esett, hogy én javítom a P.3992-est, vagy mit... jól belenyúltam.
Ha ti ketten együtt nem találtatok triviális megoldást, akkor szerintem én sem fogok összehozni semmit, majd, ha megnézem... Viszont majd megkérdezem a megoldást (ha már belefáradtam az egészbe), azt majd felteszem ide.
A pontozást majd meglátom...
|
| Előzmény: [309] Alma, 2007-06-12 21:59:48 |
|







 . Az elváláskor a félgömb már nem fejt ki erőt a kistestre és a kistest se a félgömbre, ezért egyik test sem fog gyorsulni, tehát inerciarendszereket alkalmazhatunk a feírásnál. Írjuk fel a következő egyenletet a kistest mozgására, a félgömbhöz rögzített rendszerben:
. Az elváláskor a félgömb már nem fejt ki erőt a kistestre és a kistest se a félgömbre, ezért egyik test sem fog gyorsulni, tehát inerciarendszereket alkalmazhatunk a feírásnál. Írjuk fel a következő egyenletet a kistest mozgására, a félgömbhöz rögzített rendszerben:  )-3.cos(
)-3.cos(
 0 és xy(x2-y2)=x2+y2.
0 és xy(x2-y2)=x2+y2.  , y=rsin
, y=rsin  )
)  4 és egyenlőség sin 4
4 és egyenlőség sin 4