Fórum: Lejárt határidejű KÖMAL feladatokról

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49]

Szeretnél hozzászólni? Jelentkezz be.

[373] S.Ákos	2008-03-15 22:15:42
A B. 4055.-ös feladatnál (Bizonyítsuk be, hogy minden n!-nál nem nagyobb pozitív egész szám felírható az n! legfeljebb n darab különböző osztójának összegeként.) elég könnyen kijön indukcióvan, h n>1 esetén n-1 db tag is elég. Az lenne a kérdésem, hogy ez mindig szükséges-e, vagy lehet tovább csökkenteni?

[372] Káli gúla

2008-03-12 09:18:12

A kiemelt képletben a szorzat indexelése is 0-tól kezdődik, tehát a Lucas tétel helyesen:

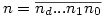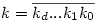Legyen n és k felírása p alapú számrendszerben (esetleg vezető nullákkal) $n=\overline{n_d...n_{1}n_0}$ és $k=\overline{k_d...k_{1}k_0}$ . Ekkor

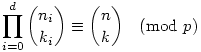
$\prod_{i=0}^{d} \binom{n_i}{k_i} \equiv \binom{n}{k} ~~~({\rm mod~} p)$

[371] Káli gúla

2008-03-12 00:20:19

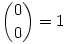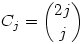Az A.445. feladat megoldása. Feltehető, hogy p páratlan, mert $\binom00=1$ miatt p=2-re az állítás triviális. Két észrevételre lesz szükség: (1) Minden mod p maradékosztály előállítható alkalmasan választott $C_j=\binom{2j}{j}$ számok szorzataként; (2) A C_j számok zártak a szorzásra, azaz ilyenek szorzata is ilyen alakú, mod p.

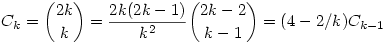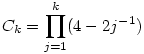(1) Mivel $C_k = \binom{2k}{k}=\frac{2k(2k-1)}{k^2}\binom{2k-2}{k-1}=(4-2/k)C_{k-1}$ , így indukcióval azt kapjuk, hogy $C_k=\prod_{j=1}^k (4-2j^{-1})$ . Belátjuk, hogy az a_j=4-2j^-1 számok közül már az első s=(p-1)/2 darab generálja az összes nem-nulla maradékosztályt. Az a_j-k nyilván j=1,...,p-1 esetén mind különbözők, és a_j=0 éppen a j=1/2=s+1-hez tartozik, ezért az a₁,a₂,...,a_s számok egymástól és 0-tól is különbözők. Legyen g primitív gyök mod p (g hatványai minden --azaz (p-1) darab-- nem-nulla maradékosztályt előállítanak). Ekkor az a₁,a₂,...,a_s elemekhez tartozó pontosan feleannyi darab kitevőre logikailag három eset lehet: 1) mind páros; 2) mind páratlan; 3) van közöttük két szomszédos. Az első eset nem fordulhat elő, mert akkor az a_j-k éppen az összes mod p négyzetszámok lennének, ami nem lehet, hiszen a 4 olyan négyzetszám, amely egyáltalán nem szerepel az a_j-k között. 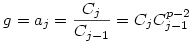A második esetben az 1 kitevőhöz tartozó j-re $g=a_j=\frac{C_j}{C_{j-1}}=C_j C_{j-1}^{p-2}$ . 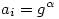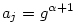A harmadik esetben van olyan i,j, hogy $a_i=g^\alpha$ és $a_j=g^{\alpha+1}$ , tehát $g=\frac{a_j}{a_i}=\frac{C_j}{C_{j-1}}\frac{C_{i-1}}{C_i}= C_j C_{j-1}^{p-2} C_{i-1} C_{i}^{p-2}$ . Így g-t, és annak hatványaival az összes nem-nulla maradékot megkaphatjuk a C_j-k hatványainak szorzataként. Hozzávéve még, hogy C_s+1=0, (1)-et teljesen igazoltuk.

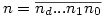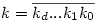(2) A bizonyításnak ez a része tulajdonképpen a binomiális együtthatókról szóló Lucas-tétel, ami a következőt mondja ki: Legyen n és k felírása p alapú számrendszerben (esetleg vezető nullákkal) $n=\overline{n_d...n_{1}n_0}$ és $k=\overline{k_d...k_{1}k_0}$ . Ekkor

$\prod_{i=1}^{d} \binom{n_i}{k_i} \equiv \binom{n}{k} ~~~({\rm mod~} p)$

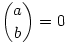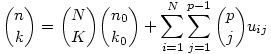(A szokásos feltevéssel $\binom{a}{b}=0$ , ha b>a.) Bizonyítás. Legyen n=Np+n₀ és k=Kp+k₀, n₀,k₀<p. Ekkor $\binom{n}{k}= \binom{N}{K} \binom{n_0}{k_0} + \sum_{i=1}^{N} \sum_{j=1}^{p-1}\binom{p}{j} u_{ij}$ , ahol u_ij egészek. Ezt úgy láthatjuk be, hogy veszünk egy N sorból és p oszlopból álló táblát, kiegészítjük egy (N+1)-edik sorral, amiben csak n₀<p mező van, és osztályozzuk ennek az n mezőnek a k elemű részhalmazait aszerint, hogy csak teljes, vagy töredék sorokat is tartalmaznak az N×p-s téglalapban. A jobb oldalon az első tag azon k elemű részhalmazok számát adja, amelyek csak teljes sorokat tartalmaznak a téglalap alakú részből (N teljes sorból kell K sort, az utolsó n₀ mezőből k₀-t venni), a kettős szumma tagjai pedig azokét, amelyekben az első töredékes sor az i-edik, és az i-edik sorral vett metszet j elemű (1 $\le$ j $\le$ p-1). 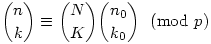Ezekben a tagokban a binomiális együttható osztható p-vel, ezért mod p a teljes szumma elhagyható: $\binom{n}{k}\equiv \binom{N}{K} \binom{n_0}{k_0} ~~({\rm mod~} p)$ . Ebből a Lucas-tétel már egyszerűen következik teljes indukcióval.

Összerakva a két segédtételt: egy r $\neq$ 0 maradékosztályt az első alapján felírhatunk $r\equiv \prod_{j=1}^{(p-1)/2} \binom{2j}{j}^{\alpha_j} ~~({\rm mod~}p)$ alakban ( $\alpha$ _j $\ge$ 0, j=1,..,(p-1)/2), majd kereshetünk egy olyan n egész számot, amelynek p-adikus felírásában a j számjegy $\alpha$ _j-szer szerepel (j=1,..,(p-1)/2). Mivel 2n felírásában az n számjegyei kétszereződnek (2j<p miatt nincs átvitel), így a (2) rész szerint

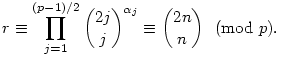
$r \equiv \prod_{j=1}^{(p-1)/2} \binom{2j}{j}^{\alpha_j}\equiv \binom{2n}{n} ~~({\rm mod~}p).$

[370] Róbert Gida

2008-02-25 00:49:29

A.444. feladat megoldása: Indirekten, ha nem teljesül az állítás, akkor létezik $\varepsilon$ >0, hogy végtelenhez tartó x_n sorozatra |f(x_n)|> $\varepsilon$ teljesül, de mivel f folytonos, ezért minden n-ra az x_n kis [u_n,w_n] környezetében is teljesül ez.

Legyen a₁=1,b₁=2, tegyük fel, hogy a_n,b_n-et már definiáltuk, hogy a_n<b_n és minden y-ra az [a_n,b_n]-ből |f(y)|> $\varepsilon$ teljesül (ha n>1). Elég nagy N₀ egészre teljesül, hogy (N₀+1)a_n<N₀b_n, ezért N $\geq$ N₀ esetén az [Na_n,Nb_n] és [(N+1)a_n,(N+1)b_n] intervallumok metszik egymást, azaz [N₀a_n, $\infty$ ) intervallumot fedik, így mivel az x_k sorozat végtelenhez tart, ezért lesz N₀a_n-nél nagyobb eleme, ami beleesik egy ilyen intervallumba, mondjuk az [Na_n,Nb_n]-be, legyen [c,d] az x_k fent definiált kis [u_k,w_k] környezetének és az előbbi intervallumnak a metszete, és $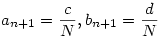a_{n+1}=\frac cN,b_{n+1}=\frac dN$ , ekkor triviálisan [a_n+1,b_n+1] része [a_n,b_n]-nek, így Cantor közös pont tétele miatt lesz az egymásba skatulyázott zárt intervallumok metszete nem üres, legyen p>0 közös pont, ekkor a konstrukció miatt p-re nem teljesül a feladat feltétele, hiszen részsorozatára nem teljesül: |f(Np)|> $\varepsilon$ , ahol N végtelenhez tartó sorozata a pozitiv egészeknek.

[369] Apa	2008-01-18 07:30:29
Köszönöm.
Előzmény: [368] nadorp, 2008-01-17 21:47:38

[368] nadorp

2008-01-17 21:47:38

Gratulálok, elegáns megoldás. Érdemes lírni.

$a+b+c=3\cdot\frac13(a+b+c)=3(ab+ac+bc)(a+b+c)$

a+b+c+a³+b³+c³-3abc=(a+b+c)³

a(a²-bc+1)+b(b²-ac+1)+c(c²-ab+1)=(a+b+c)³

$(a+b+c)^2=\frac a{a+b+c}(a^2-bc+1)+\frac b{a+b+c}(b^2-ac+1)+\frac c{a+b+c}(c^2-ab+1)$

$(a+b+c)^2\geq\frac1{\frac a{a+b+c}\frac1{a^2-bc+1}+\frac b{a+b+c}\frac1{b^2-ac+1}+\frac c{a+b+c}\frac1{c^2-ab+1}}$

$a+b+c\geq\frac1{\frac a{a^2-bc+1}+\frac b{b^2-ac+1}+\frac c{c^2-ab+1}}$

$\frac1{a+b+c}\leq\frac a{a^2-bc+1}+\frac b{b^2-ac+1}+\frac c{c^2-ab+1}$

Előzmény: [366] Apa, 2008-01-16 21:45:33

[367] Maga Péter	2008-01-17 08:10:36
És valójában a Wolstenholme-tétel is bizonyítható néhány sorban...:)
Előzmény: [362] Róbert Gida, 2007-12-18 14:46:16

[366] Apa

2008-01-16 21:45:33

Szép, bár nyilván B.4049.

Sajnos én nem tudok TEX-ben írni, de megpróbálom verbálisan "elmondani" az én megoldásomat :-)

a+b+c=a+b+c

Szorozzunk a jobb oldalon 3-mal és 1/3-dal, majd ez utóbbi tört helyére írjuk be a feladat feltételét.

Bontsuk fel jobb oldalon a zárójelet, adjunk mindkét oldalhoz hozzá aköb+bköb+cköböt és vonjunk ki mindkét oldalból 3abc-t.

Alkalmas kiemelések (a,b és c) után a bal oldalon kapjuk a bizonyítandó állítás törtjei nevezőinek rendre a-val b-vel és c-vel vett szorzatait, míg a jobb oldalon az a+b+c kifejezés köbét.

Most osszunk a+b+c-vel mindkét oldalon.

A kapott bal oldali kifejezés az előbb említett törtek nevezőinek a-val, b-vel, c-vel súlyozott számtani közepe.

Alkalmazzuk a számtani és harmonikus átlag közötti összefüggést (egyszerű számolással belátható, hogy mindhárom kifejezés pozitív), majd osszunk a+b+c-vel, végül vegyük mindkét oldal reciprokát.

Így a bizonyítandó állítást kaptuk. (Az egyenlőség feltétele is könnyen leolvasható.)

Előzmény: [365] S.Ákos, 2008-01-16 19:12:59

[365] S.Ákos

2008-01-16 19:12:59

B.5049 (jó pár lépés kihagyásával) Kicsit rendezgetve (a+b+c való szorzás és a megfelelő összevonások után kapjuk):

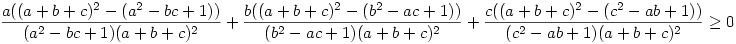
$\frac {a((a+b+c)^2-( a^2-bc+1))}{( a^2-bc+1)(a+b+c)^2}+ \frac {b((a+b+c)^2-( b^2-ac+1))}{( b^2-ac+1)(a+b+c)^2}+ \frac {c((a+b+c)^2-( c^2-ab+1))}{( c^2-ab+1)(a+b+c)^2}\ge0$

Helyettesítsük most be 1=3ab+3ac+3bc értékét, és végezzük el a műveleteket:

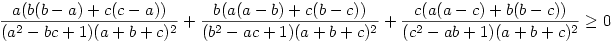
$\frac {a(b(b-a)+c(c-a))}{( a^2-bc+1)(a+b+c)^2}+ \frac {b(a(a-b)+c(b-c))}{( b^2-ac+1)(a+b+c)^2}+ \frac {c(a(a-c)+b(b-c))}{( c^2-ab+1)(a+b+c)^2}\ge0$

Hat tagra való bontás (úgy, hogy a számlálók ij(i-j) alakúak legyenek), (a+b+c)²-tel való szorzás és az ellentett számláójú törtek összevonása után kapjuk

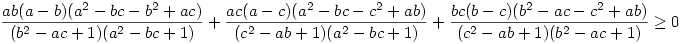
$\frac{ab(a-b)(a^2-bc-b^2+ac)}{(b^2-ac+1)(a^2-bc+1)} +\frac{ac(a-c)(a^2-bc-c^2+ab)}{(c^2-ab+1)(a^2-bc+1)}+ \frac{bc(b-c)(b^2-ac-c^2+ab)}{(c^2-ab+1)(b^2-ac+1)}\ge 0$

Szorzattá alakítva a számlálókat kapjuk:

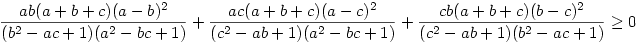
$\frac{ab(a+b+c)(a-b)^2}{(b^2-ac+1)(a^2-bc+1)} +\frac{ac(a+b+c)(a-c)^2}{(c^2-ab+1)(a^2-bc+1)}+ \frac{cb(a+b+c)(b-c)^2}{(c^2-ab+1)(b^2-ac+1)}\ge 0$

ez meg nyilván igaz, egyenlőség 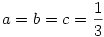$a=b=c=\frac13$ esetén.

[364] S.Ákos

2008-01-16 16:36:44

B.5051: A_n:=111...11 (5ⁿ db 1es), B_n=9A_n=10^5ⁿ-1 Prímosztókra bizonyítunk: ha p|B_n=10^5ⁿ-1, akkor p $\neq$ 2;5, így a kis-fermat tétel alapján p|10^p-1-1. Legyen r az a alegkisebb kitevő, amire p|10^r-1. Ekkor könnyen látható hogy r|p-1 és r|5ⁿ. Innét két eset van:ha r=1, akkor p=3, de A_i nem osztható 3-mal. Ha r>1, akkor 5|r, így 5|p-1 amiből 10|p-1 következik (prím nem végződhet 6-ra).így a prímosztók 10k+1 alakúak, vagyis az összes osztó ilyen alakú.

[363] Maga Péter	2007-12-24 21:25:21
Elnézést, hogy csak így beleszólok - kérdezek... a B.4020 jelű feladatnál a "poliéder" nem volt egy kicsit szerencsétlen szóhasználat, ebbe egyesek beleértik a konvexitást?

[362] Róbert Gida

2007-12-18 14:46:16

Kömal A.437 megoldása, (jó rövid lesz): D. O. Skljarszkij-N. N. Csencov-I. M. Jaglom Válogatott feladatok és tételek az elemi matematika köréből című könyv 60.a feladat szerint, ha p>3 prím, akkor 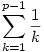$\sum_{k=1}^{p-1} \frac 1k$ összeg olyan tovább nem egyszerűsíthető tört, amelynek a számlálója osztható p²-tel. Bizonyítás a könyv végén. Ez egyébként Wolstenholme tétele.

Nekünk azonban még az $\frac 1p$ tag is benne van a feladatban, hát adjuk hozzá, kapjuk:

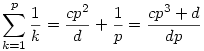
$\sum_{k=1}^{p} \frac 1k=\frac {cp^2}{d}+\frac 1p=\frac {cp^3+d}{dp}$

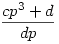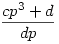, ahol persze használtam az előző feladatot és itt lnko(c,d)=1 tovább nem egyszerűsíthető felírásban. De $\frac{cp^3+d}{dp}$ sem egyszerűsíthető tovább, azaz lnko(cp³+d,dp)=1 teljesül, hiszen lnko(cp³+d,d)=lnko(cp³,d)=lnko(c,d)=1, hiszen p és d relatív prímek, mert triviálisan d osztója (p-1)!-nak, de p prím, így relatív prím (p-1)!-hoz. Továbbá lnko(cp³+d,p)=lnko(d,p)=1 az előzőek miatt szintén. Így d-hez és p-hez is relatív prímcp³+d, de akkor pd-hez is. Azaz a feladat jelöléseit használva valamely T egészre a felírás a következő alakú a=T(cp³+d) és b=T(dp) lesz, hiszen a redukált alak $\frac {cp^3+d}{dp}$ . Így

ap-b=T(cp⁴+dp-dp)=Tcp⁴

ami valóban osztható p⁴-nel. Készen vagyunk.

[361] Róbert Gida

2007-11-17 13:43:39

Kömal A. 436. megoldása: Indirekt tegyük fel, hogy n pozítiv egész és

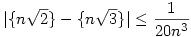
$|\{n\sqrt 2\}-\{n\sqrt 3\}|\leq \frac {1}{20n^3}$

Legyen

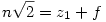$n\sqrt 2=z_1+f$

(1)

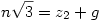$n\sqrt 3=z_2+g$

(2)

Ahol z₁ és z₂ a számok egészrészei, míg f és g a számok törtrészei. Így a feladat szerint

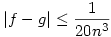$|f-g|\leq \frac {1}{20n^3}$

(3)

Vonjuk ki a (2)-es egynletből az (1)-est, kapjuk:

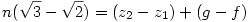
$n(\sqrt 3-\sqrt 2)=(z_2-z_1)+(g-f)$

Osszuk el n-el és legyen z₂-z₁=p egész szám, ekkor:

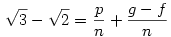
$\sqrt 3-\sqrt 2=\frac pn+\frac {g-f}n$

Kivonva az egyenletből 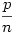$\frac pn$ -et és (3)-at használva kapjuk:

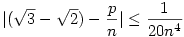$|(\sqrt 3-\sqrt 2)-\frac pn|\leq \frac{1}{20n^4}$

(4)

A háromszög-egyenlőtlenséget és (4)-et használva:

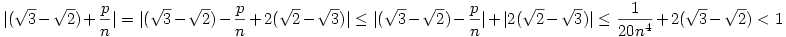
$|(\sqrt 3-\sqrt 2)+\frac pn|=|(\sqrt 3-\sqrt 2)-\frac pn+2(\sqrt 2-\sqrt 3)|\leq |(\sqrt 3-\sqrt 2)-\frac pn|+|2(\sqrt 2-\sqrt 3)|\leq \frac 1{20n^4}+2(\sqrt 3-\sqrt 2)<1$

Azaz:

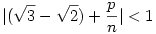$|(\sqrt 3-\sqrt 2)+\frac pn|<1$

(5)

(4)-et és (5)-öt összeszorozva, kapjuk:

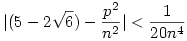$|(5-2\sqrt 6)-\frac {p^2}{n^2}|<\frac 1{20n^4}$

(6)

Újra a háromszög-egyenlőtlenséget és (6)-ot használva:

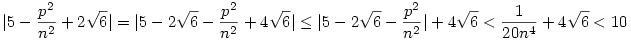
$|5-\frac {p^2}{n^2}+2\sqrt 6|=|5-2\sqrt 6-\frac {p^2}{n^2}+4\sqrt 6|\leq |5-2\sqrt 6-\frac {p^2}{n^2}|+4\sqrt 6<\frac 1{20n^4}+4\sqrt 6<10$

Azaz

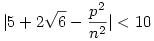$|5+2\sqrt 6-\frac {p^2}{n^2}|<10$

(7)

(6)-ot és (7)-et összeszorozva:

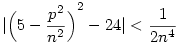$|{\Big (5-\frac{p^2}{n^2}\Big)}^2-24|<\frac 1{2n^4}$

(8)

Az egyenlőtlenséget n⁴-gyel szorozva kapjuk:

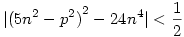
$|{(5n^2-p^2)}^2-24n^4|<\frac 12$

De a bal oldalt nemnegatív egész szám áll, így csak nulla lehet, azaz

(5n²-p²)²-24n⁴=0

Azaz

(5n²-p²)²=24n⁴

, ami nem lehet, mert bal oldalon négyzetszám áll, míg a jobb oldalon nem, amint az könnyen látható. Így ellentmondást kaptunk, így igaz a feladat állítása.

[360] sakkmath	2007-11-07 09:10:06
Mára kijavult.
Előzmény: [359] sakkmath, 2007-11-06 09:19:54

[359] sakkmath

2007-11-06 09:19:54

Az A433., szeptemberi feladat megoldása a komal.hu-n egy elírással jelent meg .

Az (1a) sor első '=' jele téves, a helyére '+' jelet kell írni.

[358] rizsesz	2007-10-31 13:04:26
Nem ismerem :) de a neve alapján nem merek nyilatkozni ilyesmikről. Tavaly a C-ben volt egy hatodikos amerikai lány, aki csak angolul küldött megoldásokat.
Előzmény: [357] jonas, 2007-10-31 12:00:23

[357] jonas	2007-10-31 12:00:23
Csak Amerikából versenyzik, vagy nem is ért magyarul?
Előzmény: [354] rizsesz, 2007-10-30 15:20:26

[356] rizsesz	2007-10-30 20:57:18
nojó :)

[355] PPP	2007-10-30 15:40:27
B $\ne$ A $\ne$ K :-)

[354] rizsesz	2007-10-30 15:20:26
Én pont most láttam egy Amerikából versenyző fiatalt az A-ban. :)

[353] Ratkó Éva	2007-10-30 13:48:41
Köszönjük, kijavítottuk. (Angol megoldó egyik versenyben sincs, legalábbis szeptemberben nem volt.)
Előzmény: [352] vogel, 2007-10-21 13:40:20

[352] vogel	2007-10-21 13:40:20
A B.4013. is rosszul volt fordítva. Ki lehet-e színezni a pozitív racionális számokat... Angolul: s it possible to colour the positive integers... Ami ugye egész számokat ír.

[351] Python

2007-10-21 13:17:30

Szerintem a mostani K.136. feladat félre van fordítva az újságban:

Magyar:

"Az iskola fiútanulóinak 70%-át az első, lánytanulóinak 80%-át a második csoportba osztották be."

Angol:

"70% of the boys and 80% of the girls were in the first group."

Mellesleg az angolt nem lehet megoldani...

[350] Kisfox

2007-08-16 09:31:06

az en nevem varga bonbien es en raktam fel az artofproblemsolvingra a feladatokat. Az A matekokat azert mert tortem rajtuk a fejemet, de nem jutottam megoldasra, igy kivancsi lettem a megoldasukra, es kertem a velemenyet a forumozoknak. Aztan ha mar kaptam tippeket gondoltam (nagyon rosszul) hogy miert ne adjak be roluk megoldast. hasonlo volt a helyzet egy par B vel. a fizikakat amiket felraktam viszont csak azutan tettem hogy megoldottam oket. a p3992 feladattal kapcsolatban meg azt tudom mondani, hogy semmifele kiszivargasrol nincsen szo. nezzetek csak meg a komal 2006 januarjaban kituzott p3860 as feladatot. lathato hogy mar akkor meg kaptam ra az 5 pontot, es az is lathato hogy ezt a feladatot tuztem ki a forumon. az meg pusztan veletlen hogy pont a majusi rakovetkezo ujsagban volt egy hasonlo feladat.

ezennel kifejezm mely sajnalatomat eme nagyon rossz tettemert, es sajnalom hogy ha a szerkesztosegnek fejfajast okoztam. Nagyon elveztem oldani a komal feladatait, es pusztan tulzott erdeklodesem okozta a vesztem.

Varga Bonbien

[349] lorantfy

2007-08-09 11:15:49

Mindegy, hogy hány lakosú a falu, ha több mint 103. Ugyanis előfordulhat, hogy a lakosok közül 103 fő alakít 104 (vagy annál több) klubot és a többi lakos nem vesz részt a klubalakításban.

$\left(\matrix{103 \cr 101 }\right)=5253$

Ez azt jelenti, hogy 103 fő akár 5253 legalább 1 tagban különböző klubot is alakíthat. Törvényes képviselője viszon csak 103-nak lehet, mert csak ennyi emberünk van.

A jogi bizottság ezért nem engedélyezheti, hogy 103-nál több klub jöjjön létre. Hiszen, ha engedélyezné 104 klub létrehozását, akkor 103 lakos összeállhatna és alakíthatna mondjuk 104 klubot és a 104. klubnál már nem lehetne törvényes képviselőt találni.

Láttuk, hogy 101 és 102 klub létrehozása engedélyezhető.

Egyetlen kérdés maradt, - és ez a feladat legszebb része - hogy 103 db klub esetén lehet-e mindig törvényes képviselőt választani.

A válasz: igen, már csak meg kell mondani hogyan!

Előzmény: [348] öreg, 2007-08-09 09:41:28

Már regisztráltál?
Új vendég vagy?