Fórum: Lejárt határidejű KÖMAL feladatokról

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49]

Szeretnél hozzászólni? Jelentkezz be.

[395] rizsesz	2008-05-26 09:58:57
Egyszerűen nem kell reagálni a hozzászólásaira, a feladataira, azt hiszem ez a legegyszerűbb megoldás.
Előzmény: [394] Sirpi, 2008-05-26 08:35:33

[394] Sirpi	2008-05-26 08:35:33
Ha gondolkodtál volna kicsit, mielőtt megint fröcsögsz, akkor rájöttél volna, hogy a feladat nincs elszúrva. Senki nem mondta, hogy minden N-re kell lennie ilyen színezésnek. Ha nincs, akkor arra az N-re az állítás üres. A stílusod viszont nem nagyon fejlődik...
Előzmény: [393] Róbert Gida, 2008-05-26 00:58:52

[393] Róbert Gida

2008-05-26 00:58:52

"A.448. helyett új példát tűztek ki."

No igen. De ezt is sikerült elszúrniuk: "A. 448. Az 1,2,...,N számokat kiszíneztük 3 színnel úgy, hogy mindegyik szín legfeljebb 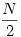$\frac{N}{2}$ -ször szerepel."

N=1-re egy lehetséges színezést azért megnéznék...

Előzmény: [389] Róbert Gida, 2008-05-08 16:58:43

[392] Python	2008-05-18 17:56:28
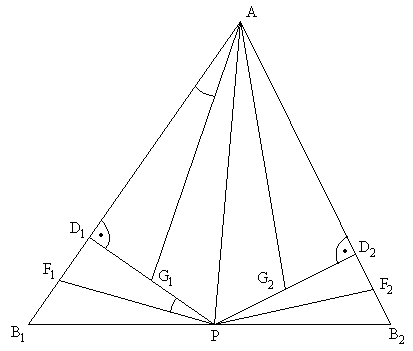
Legyen PD₁ felezőpontja G₁, PD₂ felezőpontja G₂! Mivel A felezi PQ-t, AG₁ középvonal PQD₁ hároszögben, így AG₁ párhuzamos QD₁-el. Hasonlóan AG₂ párhuzamos QD₂-vel. Tegyük fel, hogy QD₁-merőleges PF₁-re! Ekkor AG₁ is merőleges PF₁-re. Mivel PD₁ merőleges AD₁-re, így F₁PD₁ $\angle$ és G₁AD₁ $\angle$ szögek megegyeznek (merőleges szárú szögek). Így F₁PD₁ és G₁AD₁ háromszögek hasonlóak, mivel a szögeik megegyeznek. 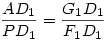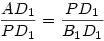Így $\frac{AD_1}{PD_1}=\frac{G_1D_1}{F_1D_1}$ , de így, mivel PD₁=2G₁D₁ és D₁B₁=2F₁D₁, $\frac{AD_1}{PD_1}=\frac{PD_1}{B_1D_1}$ , ami azt jelenti, hogy AD₁P és PD₁B₁ derékszögű háromszögek is hasonlóak. Így pl. D₁PB₁ $\angle$ =D₁AP $\angle$ =90^o-D₁PA $\angle$ , és emiatt B₁PA $\angle$ =90^o, ami azt jelenti, hogy AP a háromszög A-ból induló magassága, P a magasságtalppont B₁B₂-n (mivel a háromszög hegyesszögű, ez B₁B₂ szakaszon van). Innen visszfelé ugyanez elmondható a másik oldalon, ami miatt teljesül a feladat állítása. 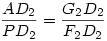(APB₂ $\angle$ =90^o, így AD₂P és PD₂B₂ hasonló, mivel PAD₂ $\angle$ =90^o-APD₂ $\angle$ =D₂PB₂ $\angle$ , így AD₂G₂ és PD₂F₂ is hasonló ( $\frac{AD_2}{PD_2}=\frac{G_2D_2}{F_2D_2}$ miatt), de ekkor G₂AD₂ $\angle$ =F₂PD₂ $\angle$ , és ebből, valamint PD₂ és AD₂ merőlegességéből következik, hogy AG₂ merőleges PF₂-re, így QD₂ merőleges PF₂-re, és ezt kellett igazolni.) A lényeg az, hogy ha van két hasonló háromszögünk, és mindkettőt "félbevágjuk" egymásnak megfelelő csúcsaikból induló súlyvonalakkal, akkor a megfelelő részháromszögek is hasonlóak lesznek. Ezt itt csak derékszögű háromszögekre igazoltam és használtam fel.

Előzmény: [390] S.Ákos, 2008-05-17 09:21:05

[391] BohnerGéza	2008-05-17 16:58:02


Előzmény: [390] S.Ákos, 2008-05-17 09:21:05

[390] S.Ákos	2008-05-17 09:21:05
Valaki tudna mutatni egy elemi geometriai megoldást a B.4088-as feladatra?

[389] Róbert Gida	2008-05-08 16:58:43
A.448. helyett új példát tűztek ki.
Előzmény: [382] Róbert Gida, 2008-03-27 01:02:18

[388] rizsesz

2008-04-16 14:22:44

Nagyon szép megoldás, kedves Ákos (bár eléggé adta magát a kis Fermat-tétel :)).

Néhány gondolat amúgy eszembe jutott a kitűzött K problémákkal kapcsolatban.

A K. 167. ugyanabba a hibába esik, mint a K. 90.

Azt kérte ott ugyanis a feladat, hogy adjunk meg minél több megoldást, míg maximális pont arra járt, ha igazoltad, hogy két megoldás van és nincsen több. Érdemes lenne ezt a javítóknak most is figyelembe venni, és ilyen hibába nem beleesni újra.

A másik a K. 168. Ennek második része pedig már korábban tárgyalt B feladat (azt hiszem 2002 - 2003 májusi). Ez persze nem először fordul elő, de úgy gondolom, hogy ilyenekre érdemes lenne ügyelni.

Üdv, rizs

[387] S.Ákos	2008-04-16 12:20:38
helyesen: (n,a-1) $\ge$ p>1
Előzmény: [386] S.Ákos, 2008-04-16 12:19:37

[386] S.Ákos

2008-04-16 12:19:37

B.4078. Legyen p n legkisebb prímosztója, k pedig a rendje mod p. Ekkor a feltételek alapján (i) (p,a)=1 (ii)k|n és (iii)k<p (ez a Kis-Fermat tételből és (i)-ből következik, mivel ekkor p|a^p-1-1). Mivel p n legkisebb prímosztója, így a [2;p-1] intervallumban nem oszthatja egy szám sem, mivel ez ellentmondana p minimalitásának. $\implies$ k=1, így p|a-1 $\implies$ (a-1,n)=p>1

[385] kdano	2008-03-30 23:06:35
Ez sem igaz. Laci n=5-ig küldött ellenpéldát. n=8-tól viszont már igaz az állítás.
Előzmény: [383] rizsesz, 2008-03-27 08:23:15

[384] rizsesz	2008-03-27 08:23:36
2ⁿ-1-et.

[383] rizsesz	2008-03-27 08:23:15
de n>3-ra már jó, csak akkor nem A-nak való ez a feladat. (bár lehet, hogy van olyan konstrukció, ami még jobban szűkíti a 2ⁿ/2-t.
Előzmény: [382] Róbert Gida, 2008-03-27 01:02:18

[382] Róbert Gida

2008-03-27 01:02:18

Javítás: rossz volt az ellenpélda:

n=1-re: S=A, teljesíti a feltételeket, de |S|=1<3*1, ellentmondás. Megjegyzem, hogy n=1 esetén S más nem is lehet, hogy teljesítse a feltételeket, az |S|=3 álom.

n=2-re: a legkisebb S ellenpélda: S=AA,AB,BA, erre |S|=3<2*3, ellentmondás.

n=3-ra egy ellenpélda (lehet, hogy nem a legkisebb): S=AAA,AAB,ABA,ABB,BAA,BAB,BBA (látszik a minta?), itt |S|=7<3*3, ellentmondás.

Sokat nem foglalkozott a példával a kitűző, vagy csak sajtóhiba. Ezt gondolom a Fazekasban egyből kiszúrták.

Előzmény: [381] Róbert Gida, 2008-03-27 00:39:19

[381] Róbert Gida

2008-03-27 00:39:19

A.448

AHA, igazad van. Ilyen rossz feladatot régen olvastam. n=1-re biztosan nem igaz: Legyen S="B","C" ez teljesíti a feltételeket, de |S|=2<3, ellentmondás.

Egyébként amit én kb. 5 perc alatt találtam: n>12-re az állítás biztosan igaz! Sőt az alsó korlát ultragyenge. Ok: 1 darab n hosszú S-beli szó 3ⁿ darab szót tilt le W-ből, hiszen 1 pozicióra 3 lehetőség van és n pozició van, Így legfeljebb |S|*3ⁿ darab szót tudunk letiltani, aminek nagyobb vagy egyenlőnek kell lennie, mint -1+4ⁿ, hiszen ennyien vannak az n hosszú szavak, a csupa "A" nélkül. Azaz |S|*3ⁿ 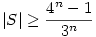$\geq$ -1+4ⁿ, tehát $|S|\geq \frac {4^n-1}{3^n}$ . Ez pedig n>12-re indukcióval belátható, hogy legalább 3*n, ami kellettt, sőt a becslés szerint S-nek exponenciálisan sok eleme van, így a feladat lineáris becslése nudli.

Előzmény: [380] kdano, 2008-03-26 21:21:43

[380] kdano	2008-03-26 21:21:43
Annak a feladatnak az állítása nem igaz..
Előzmény: [379] ik68, 2008-03-26 13:50:06

[379] ik68	2008-03-26 13:50:06
Ha lenne valakinek egy megoldasa az A.448.-as feladatra, örömmel venném. Köszönöm!

[378] nadorp	2008-03-21 15:26:41
Igaz. A vége nem kell, elbonyolítottam.
Előzmény: [377] Lóczi Lajos, 2008-03-21 14:28:20

[377] Lóczi Lajos	2008-03-21 14:28:20
De miért kell integrálra hivatkozni? Nem elég az, hogy ha egy függvény deriváltja nemnegatív, akkor a függvény nemcsökkenő?
Előzmény: [376] nadorp, 2008-03-21 10:20:26

[376] nadorp

2008-03-21 10:20:26

A.447

A feladat következő általánosítását bizonyítjuk be:

Legyenek a₁,...,a_n tetszőleges valós számok és b₁,...,b_n tetszőleges pozitív valós számok. Ekkor 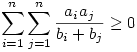$\sum_{i=1}^{n}\sum_{j=1}^{n}\frac{a_ia_j}{b_i+b_j}\geq0$ Bizonyítás:

Legyen 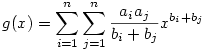$g(x)=\sum_{i=1}^{n}\sum_{j=1}^{n}\frac{a_ia_j}{b_i+b_j} x^{b_i+b_j}$ (x $\geq$ 0). Azt kell bizonyítani, hogy g(1) $\geq$ 0

Nyilván g(0)=0. Továbbá a függvény deriváltjára

g^'(x) 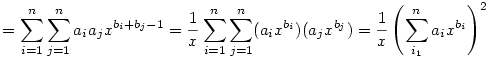$=\sum_{i=1}^{n}\sum_{j=1}^{n}a_ia_jx^{b_i+b_j-1}= \frac1x\sum_{i=1}^{n}\sum_{j=1}^{n}(a_ix^{b_i})(a_jx^{b_j})= \frac1x\left(\sum_{i_1}^{n}a_ix^{b_i}\right)^2$

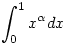Mivel $\alpha$ >-1 esetén $\int_0^1x^\alpha dx$ létezik , ezért b_i+b_j-1>-1 miatt g^' integrálható a [0;1] intervallumon és a fentiek miatt g^'(x) $\geq$ 0. Tehát

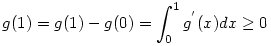$g(1)=g(1)-g(0)=\int_0^1g^{'}(x)dx\geq0$ , hiszen nemnegatív függvény integrálja is nemnegatív.

[375] sakkmath	2008-03-18 17:16:02
A B. 4056. feladat itt olvasható rapid megoldásával kapcsolatban megjegyzem, hogy létezik tisztán elemi geometriai megoldás is, amely - esetleg - érdekesebb fordulatokat ígér...

[374] nadorp

2008-03-16 11:30:21

A.443

Nevezzük a p kerületű hatszöget H-nak, csúcsai legyenek A,B,C,D,E,F és nevezzük az oldalfelező pontok által meghatározott hatszöget H₁-nek az F_i ( i=1...6) csúcsokkal. Húzzuk be az AC,BD,...,FB átlókat. Ezen átlók metszéspontjai H belsejében egy olyan H₂ hatszöget határoznak meg, melynek oldalai nyilván párhuzamosak H₁ egy-egy oldalával ( melyek középvonalak), tehát H₂ szögei szintén 120^o-sak. Ebből következik, hogy az AEC és BDF háromszögek minden szöge 60^o, tehát ezek a háromszögek szabályosak. Mivel H₂ szemközti oldalai nyilván párhuzamosak is, ezért H csúcsait úgy kaphatjuk meg, hogy H₂ oldalaira kifelé egy-egy szabályos háromszöget állítunk. Legyenek H₂ oldalai a₁,...,a₆ hosszúak. Ekkor

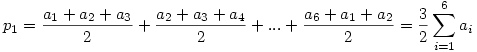$p_1=\frac{a_1+a_2+a_3}2+\frac{a_2+a_3+a_4}2+...+ \frac{a_6+a_1+a_2}2=\frac32\sum_{i=1}^6{a_i}$ .

Másrészt 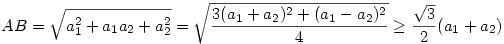$AB=\sqrt{a_1^2+a_1a_2+a_2^2}=\sqrt{\frac{3(a_1+a_2)^2+ (a_1-a_2)^2}4}\geq\frac{\sqrt3}2(a_1+a_2)$

Ha ezt elvégezzük H mindegyik oldalára akkor az kapjuk, hogy

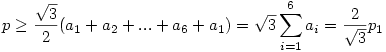
$p\geq\frac{\sqrt3}2(a_1+a_2+...+a_6+a_1)= \sqrt3\sum_{i=1}^6{a_i}=\frac2{\sqrt3}p_1$

[373] S.Ákos	2008-03-15 22:15:42
A B. 4055.-ös feladatnál (Bizonyítsuk be, hogy minden n!-nál nem nagyobb pozitív egész szám felírható az n! legfeljebb n darab különböző osztójának összegeként.) elég könnyen kijön indukcióvan, h n>1 esetén n-1 db tag is elég. Az lenne a kérdésem, hogy ez mindig szükséges-e, vagy lehet tovább csökkenteni?

[372] Káli gúla

2008-03-12 09:18:12

A kiemelt képletben a szorzat indexelése is 0-tól kezdődik, tehát a Lucas tétel helyesen:

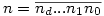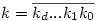Legyen n és k felírása p alapú számrendszerben (esetleg vezető nullákkal) $n=\overline{n_d...n_{1}n_0}$ és $k=\overline{k_d...k_{1}k_0}$ . Ekkor

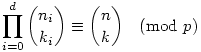
$\prod_{i=0}^{d} \binom{n_i}{k_i} \equiv \binom{n}{k} ~~~({\rm mod~} p)$

[371] Káli gúla

2008-03-12 00:20:19

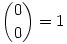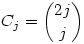Az A.445. feladat megoldása. Feltehető, hogy p páratlan, mert $\binom00=1$ miatt p=2-re az állítás triviális. Két észrevételre lesz szükség: (1) Minden mod p maradékosztály előállítható alkalmasan választott $C_j=\binom{2j}{j}$ számok szorzataként; (2) A C_j számok zártak a szorzásra, azaz ilyenek szorzata is ilyen alakú, mod p.

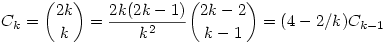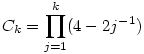(1) Mivel $C_k = \binom{2k}{k}=\frac{2k(2k-1)}{k^2}\binom{2k-2}{k-1}=(4-2/k)C_{k-1}$ , így indukcióval azt kapjuk, hogy $C_k=\prod_{j=1}^k (4-2j^{-1})$ . Belátjuk, hogy az a_j=4-2j^-1 számok közül már az első s=(p-1)/2 darab generálja az összes nem-nulla maradékosztályt. Az a_j-k nyilván j=1,...,p-1 esetén mind különbözők, és a_j=0 éppen a j=1/2=s+1-hez tartozik, ezért az a₁,a₂,...,a_s számok egymástól és 0-tól is különbözők. Legyen g primitív gyök mod p (g hatványai minden --azaz (p-1) darab-- nem-nulla maradékosztályt előállítanak). Ekkor az a₁,a₂,...,a_s elemekhez tartozó pontosan feleannyi darab kitevőre logikailag három eset lehet: 1) mind páros; 2) mind páratlan; 3) van közöttük két szomszédos. Az első eset nem fordulhat elő, mert akkor az a_j-k éppen az összes mod p négyzetszámok lennének, ami nem lehet, hiszen a 4 olyan négyzetszám, amely egyáltalán nem szerepel az a_j-k között. 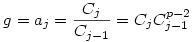A második esetben az 1 kitevőhöz tartozó j-re $g=a_j=\frac{C_j}{C_{j-1}}=C_j C_{j-1}^{p-2}$ . 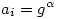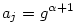A harmadik esetben van olyan i,j, hogy $a_i=g^\alpha$ és $a_j=g^{\alpha+1}$ , tehát $g=\frac{a_j}{a_i}=\frac{C_j}{C_{j-1}}\frac{C_{i-1}}{C_i}= C_j C_{j-1}^{p-2} C_{i-1} C_{i}^{p-2}$ . Így g-t, és annak hatványaival az összes nem-nulla maradékot megkaphatjuk a C_j-k hatványainak szorzataként. Hozzávéve még, hogy C_s+1=0, (1)-et teljesen igazoltuk.

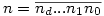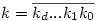(2) A bizonyításnak ez a része tulajdonképpen a binomiális együtthatókról szóló Lucas-tétel, ami a következőt mondja ki: Legyen n és k felírása p alapú számrendszerben (esetleg vezető nullákkal) $n=\overline{n_d...n_{1}n_0}$ és $k=\overline{k_d...k_{1}k_0}$ . Ekkor

$\prod_{i=1}^{d} \binom{n_i}{k_i} \equiv \binom{n}{k} ~~~({\rm mod~} p)$

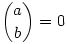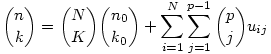(A szokásos feltevéssel $\binom{a}{b}=0$ , ha b>a.) Bizonyítás. Legyen n=Np+n₀ és k=Kp+k₀, n₀,k₀<p. Ekkor $\binom{n}{k}= \binom{N}{K} \binom{n_0}{k_0} + \sum_{i=1}^{N} \sum_{j=1}^{p-1}\binom{p}{j} u_{ij}$ , ahol u_ij egészek. Ezt úgy láthatjuk be, hogy veszünk egy N sorból és p oszlopból álló táblát, kiegészítjük egy (N+1)-edik sorral, amiben csak n₀<p mező van, és osztályozzuk ennek az n mezőnek a k elemű részhalmazait aszerint, hogy csak teljes, vagy töredék sorokat is tartalmaznak az N×p-s téglalapban. A jobb oldalon az első tag azon k elemű részhalmazok számát adja, amelyek csak teljes sorokat tartalmaznak a téglalap alakú részből (N teljes sorból kell K sort, az utolsó n₀ mezőből k₀-t venni), a kettős szumma tagjai pedig azokét, amelyekben az első töredékes sor az i-edik, és az i-edik sorral vett metszet j elemű (1 $\le$ j $\le$ p-1). 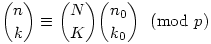Ezekben a tagokban a binomiális együttható osztható p-vel, ezért mod p a teljes szumma elhagyható: $\binom{n}{k}\equiv \binom{N}{K} \binom{n_0}{k_0} ~~({\rm mod~} p)$ . Ebből a Lucas-tétel már egyszerűen következik teljes indukcióval.

Összerakva a két segédtételt: egy r $\neq$ 0 maradékosztályt az első alapján felírhatunk $r\equiv \prod_{j=1}^{(p-1)/2} \binom{2j}{j}^{\alpha_j} ~~({\rm mod~}p)$ alakban ( $\alpha$ _j $\ge$ 0, j=1,..,(p-1)/2), majd kereshetünk egy olyan n egész számot, amelynek p-adikus felírásában a j számjegy $\alpha$ _j-szer szerepel (j=1,..,(p-1)/2). Mivel 2n felírásában az n számjegyei kétszereződnek (2j<p miatt nincs átvitel), így a (2) rész szerint

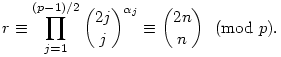
$r \equiv \prod_{j=1}^{(p-1)/2} \binom{2j}{j}^{\alpha_j}\equiv \binom{2n}{n} ~~({\rm mod~}p).$

Már regisztráltál?
Új vendég vagy?