| [398] Káli gúla | 2008-06-12 20:25:55 |
 A. 454. Létezik-e olyan konstanstól különböző valós együtthatós p polinom, amelyre minden x valós szám esetén p2(x)-1=p(x2+1) teljesül?
Nem létezik. (1) Először lássuk be, hogy minden n>0 esetén pontosan egy n-edfokú p(x) polinom létezik, amelyre 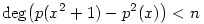 . Bizonyítás. Ilyen p polinom csak a főtaggal azonos paritású x hatványokat tartalmazhat, egyébként p2(x)-ben n-nél nem kisebb páratlan kitevős tag is adódna, ami . Bizonyítás. Ilyen p polinom csak a főtaggal azonos paritású x hatványokat tartalmazhat, egyébként p2(x)-ben n-nél nem kisebb páratlan kitevős tag is adódna, ami 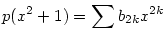 miatt lehetetlen. Legyen miatt lehetetlen. Legyen 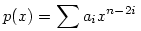 , ekkor a követelmény szerint: , ekkor a követelmény szerint:
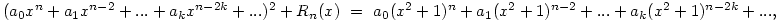
ahol Rn(x) foka kisebb, mint n. Innen az a0, a1, . . . értékeket egymás után megkaphatjuk, ha az x2n, x2n-2 . . . együtthatóit a két oldalon összehasonlítjuk. Így a0=1, 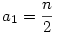 , , 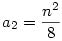 , , 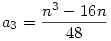 . . . Általában, ha i<k indexekre már ismerjük az ai értékeket, akkor az x2n-2k együtthatója a bal oldalon 2ak+ . . . Általában, ha i<k indexekre már ismerjük az ai értékeket, akkor az x2n-2k együtthatója a bal oldalon 2ak+ (a1,...ak-1), a jobb oldalon pedig (a1,...ak-1), a jobb oldalon pedig  (a1,...ak-1) lesz, ahonnan ak egyértelműen kiszámolható. (a1,...ak-1) lesz, ahonnan ak egyértelműen kiszámolható.
(2) Jelöljük a fentiek miatt egyértelműen meghatározott n-edfokú polinomot Hn-nel, a maradékát Rn-nel, azaz legyen 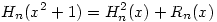 , ahol deg Rn<n. Ekkor , ahol deg Rn<n. Ekkor 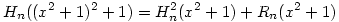 is teljesül, azaz H2n, R2n egyértelműsége és is teljesül, azaz H2n, R2n egyértelműsége és 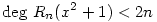 miatt azt kapjuk, hogy miatt azt kapjuk, hogy 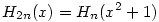 és és 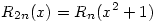 . Tehát a kiinduló állítást elég páratlan fokú p polinomokra igazolni, hiszen . Tehát a kiinduló állítást elég páratlan fokú p polinomokra igazolni, hiszen 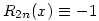 -ből -ből 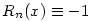 is következne. is következne.
(3) Indirekt tegyük fel, hogy p(x) páratlan fokú és teljesül rá a 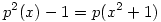 azonosság. Írjuk át ezt a azonosság. Írjuk át ezt a 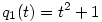 és és 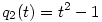 jelölésekkel jelölésekkel 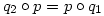 alakba. Teljes indukcióval (a q-kat egymás után "áthúzva" p-n) azonnal adódik, hogy alakba. Teljes indukcióval (a q-kat egymás után "áthúzva" p-n) azonnal adódik, hogy
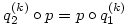
Vizsgáljuk a két oldalt az x=0 helyen k  esetén! A jobb oldalon q1(k)(0) esetén! A jobb oldalon q1(k)(0) k, hiszen indukcióval k, hiszen indukcióval ![\matrix{}q_1^{(k+1)}(0)=\big[q_1^{(k)}(0)\big]^2+1 \ge k+1](keplet.cgi?k=A8861E60FE13FFE2) , ezért , ezért 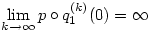 . A bizonyítás elején tett megjegyzés szerint p(0)=0, mert p minden tagja páratlan fokú, ezért a bal oldal x=0-ban egy kettő hosszúságú ciklusba van zárva, vagy 0, vagy -1, mert . A bizonyítás elején tett megjegyzés szerint p(0)=0, mert p minden tagja páratlan fokú, ezért a bal oldal x=0-ban egy kettő hosszúságú ciklusba van zárva, vagy 0, vagy -1, mert 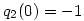 és és 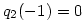 . Ez az ellentmondás igazolja az állítást. . Ez az ellentmondás igazolja az állítást.
Megjegyzés. Ugyanígy látható be, hogy a 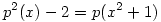 azonosság sem teljesülhet semmilyen p polinomra, csak ekkor az utolsó képlet bal oldalán a q2(t)=t2-2 polinom iteráltjai nem oszcillálnak, hanem azonosan 2 értékűek a 0 helyen, de ez is lehetetlen végtelenbe tartó jobb oldal mellett. azonosság sem teljesülhet semmilyen p polinomra, csak ekkor az utolsó képlet bal oldalán a q2(t)=t2-2 polinom iteráltjai nem oszcillálnak, hanem azonosan 2 értékűek a 0 helyen, de ez is lehetetlen végtelenbe tartó jobb oldal mellett.
|
|
| [397] jenei.attila | 2008-06-12 10:29:26 |
 Az előzőhöz javítás: "Figyelembe véve, hogy tn=0, azaz un=8" helyesen: Figyelembe véve, hogy t3=0, azaz u3=8.
A 2.a.) ponthoz kiegészítés: itt azt állítom, hogy a PP' átmérő pontosan akkor döfi át a maradék n pont által meghatározott konvex burkot, ha az n pont husszúsági koordinátáiból az egyenlítő mentén képződő n oldalú sokszög tartalmazza a gömb középpontját. Elég ezt belátni n=3 esetén, ugyanis ha PP' átdöfi a burkot, akkor az n pontból kiválasztható 3, amelyek által alkotott háromszöglemezt szintén átdöf. Fordítva, ha ilyen háromszöhlemezt átdöf, akkor a burkot is. Mindez a konvex burok tulajdonsága miatt van így. Ha pedig egy háromszög lemezt átdöf az átmérő, akkor nyilván a három pont hosszúsági koordinátáiból az egyenlítő mentén képződő háromszög tartalmazza a gömb középpontját. Ez esetben maga az egyenlítő mentén keletkező n szög is tartalmazza a gömb középpontját. Továbbá az is világos, hogy a szóbanforgó 3 ponthoz hozzávéve vagy a P, vagy a P' pontot, a keletkező tetraéderek pontosan egyike fogja tartalmazni a gömb középpontját, hiszen a három pontból, és a P és P'-ből álló 5 pontú konvex burok teljes egészében tartalmazza a PP' átmérőt (és ezzel együtt a gömb kp.-ját is).
|
|
| [396] jenei.attila | 2008-06-11 22:32:35 |
 Az A.453 feladatra írok egy megoldást. A gömbfelületen egymástól függetlenül véletlenszerűen kiválasztunk n pontot. Mi a val.-ge, hogy a kiválasztott pontok konvex burka tartalmazza a gömb középpontját?
Megoldás: Válasszuk ki a pontokat a következőképpen. Először adjunk meg n véletlenszerűen választott átmérőt. Egy átmérő a gömbfelületet két pontban döfi, amelyek egyikét választjuk pontként. Így az átmérők kijelölése után 2n lehetőség van a pontok kiválasztására. Össze fogjuk számolni, hogy a 2n lehetőségből hány olyan van, amikor a kiválasztott pontok konvex burka tartalmazza a gömb középpontját (mint látni fogjuk, ez független az átmérők helyzetétől). Jelöljük ezt tn-nel, ekkor a keresett val.-ég 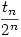 . tn+1-re egy rekurzív összefüggést adunk meg. Jelöljük ki az egyik átmérőt (PP'), és vizsgáljuk ennek, valamint a maradék n pont által meghatározott konvex buroknak a helyzetét. Három esetet különböztetünk meg: . tn+1-re egy rekurzív összefüggést adunk meg. Jelöljük ki az egyik átmérőt (PP'), és vizsgáljuk ennek, valamint a maradék n pont által meghatározott konvex buroknak a helyzetét. Három esetet különböztetünk meg:
1.) A maradék n pont konvex burka tartalmazza a gömb középpontját.
2.a.) A maradék n pont konvex burka nem tartalmazza a gömb középpontját, és nincs közös pontja a PP' átmérővel.
2.b.) A maradék n pont konvex burka nem tartalmazza a gömb középpontját, de a PP' átmérő döfi a burkot.
Az 1.) esetben akár a P, akár a P' potot választjuk a már kiválasztott n pont mellé, az új konvex burok szintén tartalmazni fogja a gömb kp.-ját. Tehát az ebből adódó kedvező esetek száma 2tn.
A 2.a.) eset akkor állhat fenn, ha a maradék n pont "hosszúsági koordinátáiból" az egyenlítő mentén keletkező n oldalú sokszög nem tartalmazza a gömb kp.-ját (PP'-őt tekintjük forgástengelynek, az erre merőleges főkör az egyenlítő). Tehát meg kell oldani az analóg síkbeli feladatot: a körben véletlenszerűen kiválasztva n átmérőt, majd az egyes átmérők egyik végpontját kijelölve, hány esetben nem fogja tartalmazni a kör kp.-ját a kijelölt pontokból álló n oldalú sokszög (vagyis mikor esnek egy félkörre)? Erre a válasz 2n, ami könnyen belátható. Tehát a 2.a.) pontnak megfelelő esetek száma 2n. Ezen esetekben a P vagy P' hozzávételekor keletkező konvex burok sem tatalmazza a gömb kp.-ját.
A 2.b.) esetek száma nyilván az összes esetek száma - 1.)esetek száma - 2.a.) esetek száma, vagyis 2n-tn-2n. A 2.b.) esetben, azonban a P vagy P' (kizáró vagy) hozzávételével a keletkező konvex burok tartalmazni fogja a gömb kp.-ját, hiszen PP' átdöfi a maradék konvex burkot. Tehát az összes kedvező esetek száma:
tn+1=2tn+2n-tn-2n=2n+tn-2n
. Ezzel a feladat tulajdonképpen meg van oldva, már csak a tn-re adunk egy zárt képletet. Legyen un:=2n-tn, vagyis azon esetek száma, amikor a konvex burok nem tartalmazza a gömb kp.-ját. Tehát
un+1=2n+1-tn+1=2n-tn+2n=un+2n
Figyelembe véve, hogy tn=0, azaz un=8, kapjuk, hogy
un=n2-n+2
. Vagyis a feladatra a válasz:
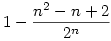
annak a valószínűsége, hogy a gömb kp-ja benne lesz a véletlenszerűen választott n pont által meghatározott konvex burokban.
|
|
|
| [394] Sirpi | 2008-05-26 08:35:33 |
 Ha gondolkodtál volna kicsit, mielőtt megint fröcsögsz, akkor rájöttél volna, hogy a feladat nincs elszúrva. Senki nem mondta, hogy minden N-re kell lennie ilyen színezésnek. Ha nincs, akkor arra az N-re az állítás üres. A stílusod viszont nem nagyon fejlődik...
|
| Előzmény: [393] Róbert Gida, 2008-05-26 00:58:52 |
|
| [393] Róbert Gida | 2008-05-26 00:58:52 |
 "A.448. helyett új példát tűztek ki."
No igen. De ezt is sikerült elszúrniuk: "A. 448. Az 1,2,...,N számokat kiszíneztük 3 színnel úgy, hogy mindegyik szín legfeljebb 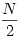 -ször szerepel." -ször szerepel."
N=1-re egy lehetséges színezést azért megnéznék...
|
| Előzmény: [389] Róbert Gida, 2008-05-08 16:58:43 |
|
| [392] Python | 2008-05-18 17:56:28 |
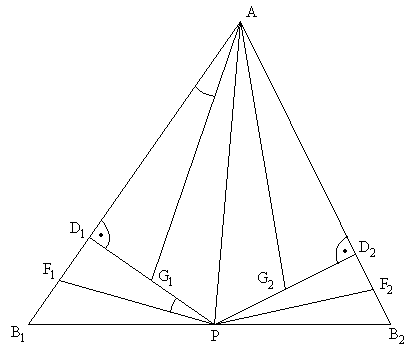
 Legyen PD1 felezőpontja G1, PD2 felezőpontja G2! Mivel A felezi PQ-t, AG1 középvonal PQD1 hároszögben, így AG1 párhuzamos QD1-el. Hasonlóan AG2 párhuzamos QD2-vel.
Tegyük fel, hogy QD1-merőleges PF1-re! Ekkor AG1 is merőleges PF1-re. Mivel PD1 merőleges AD1-re, így F1PD1 és G1AD1 és G1AD1 szögek megegyeznek (merőleges szárú szögek). Így F1PD1 és G1AD1 háromszögek hasonlóak, mivel a szögeik megegyeznek. Így szögek megegyeznek (merőleges szárú szögek). Így F1PD1 és G1AD1 háromszögek hasonlóak, mivel a szögeik megegyeznek. Így 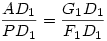 , de így, mivel PD1=2G1D1 és D1B1=2F1D1, , de így, mivel PD1=2G1D1 és D1B1=2F1D1, 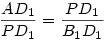 , ami azt jelenti, hogy AD1P és PD1B1 derékszögű háromszögek is hasonlóak. Így pl. D1PB1 , ami azt jelenti, hogy AD1P és PD1B1 derékszögű háromszögek is hasonlóak. Így pl. D1PB1 =D1AP =D1AP =90o-D1PA =90o-D1PA , és emiatt B1PA , és emiatt B1PA =90o, ami azt jelenti, hogy AP a háromszög A-ból induló magassága, P a magasságtalppont B1B2-n (mivel a háromszög hegyesszögű, ez B1B2 szakaszon van). =90o, ami azt jelenti, hogy AP a háromszög A-ból induló magassága, P a magasságtalppont B1B2-n (mivel a háromszög hegyesszögű, ez B1B2 szakaszon van).
Innen visszfelé ugyanez elmondható a másik oldalon, ami miatt teljesül a feladat állítása. (APB2 =90o, így AD2P és PD2B2 hasonló, mivel PAD2 =90o, így AD2P és PD2B2 hasonló, mivel PAD2 =90o-APD2 =90o-APD2 =D2PB2 =D2PB2 , így AD2G2 és PD2F2 is hasonló ( , így AD2G2 és PD2F2 is hasonló (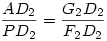 miatt), de ekkor G2AD2 miatt), de ekkor G2AD2 =F2PD2 =F2PD2 , és ebből, valamint PD2 és AD2 merőlegességéből következik, hogy AG2 merőleges PF2-re, így QD2 merőleges PF2-re, és ezt kellett igazolni.) , és ebből, valamint PD2 és AD2 merőlegességéből következik, hogy AG2 merőleges PF2-re, így QD2 merőleges PF2-re, és ezt kellett igazolni.)
A lényeg az, hogy ha van két hasonló háromszögünk, és mindkettőt "félbevágjuk" egymásnak megfelelő csúcsaikból induló súlyvonalakkal, akkor a megfelelő részháromszögek is hasonlóak lesznek. Ezt itt csak derékszögű háromszögekre igazoltam és használtam fel.
|
 |
| Előzmény: [390] S.Ákos, 2008-05-17 09:21:05 |
|
|
| [390] S.Ákos | 2008-05-17 09:21:05 |
 Valaki tudna mutatni egy elemi geometriai megoldást a B.4088-as feladatra?
|
|
|
| [388] rizsesz | 2008-04-16 14:22:44 |
 Nagyon szép megoldás, kedves Ákos (bár eléggé adta magát a kis Fermat-tétel :)).
Néhány gondolat amúgy eszembe jutott a kitűzött K problémákkal kapcsolatban.
A K. 167. ugyanabba a hibába esik, mint a K. 90.
Azt kérte ott ugyanis a feladat, hogy adjunk meg minél több megoldást, míg maximális pont arra járt, ha igazoltad, hogy két megoldás van és nincsen több. Érdemes lenne ezt a javítóknak most is figyelembe venni, és ilyen hibába nem beleesni újra.
A másik a K. 168. Ennek második része pedig már korábban tárgyalt B feladat (azt hiszem 2002 - 2003 májusi). Ez persze nem először fordul elő, de úgy gondolom, hogy ilyenekre érdemes lenne ügyelni.
Üdv, rizs
|
|
|
|
|
|
|
| [382] Róbert Gida | 2008-03-27 01:02:18 |
 Javítás: rossz volt az ellenpélda:
n=1-re: S=A, teljesíti a feltételeket, de |S|=1<3*1, ellentmondás. Megjegyzem, hogy n=1 esetén S más nem is lehet, hogy teljesítse a feltételeket, az |S|=3 álom.
n=2-re: a legkisebb S ellenpélda: S=AA,AB,BA, erre |S|=3<2*3, ellentmondás.
n=3-ra egy ellenpélda (lehet, hogy nem a legkisebb): S=AAA,AAB,ABA,ABB,BAA,BAB,BBA (látszik a minta?), itt |S|=7<3*3, ellentmondás.
Sokat nem foglalkozott a példával a kitűző, vagy csak sajtóhiba. Ezt gondolom a Fazekasban egyből kiszúrták.
|
| Előzmény: [381] Róbert Gida, 2008-03-27 00:39:19 |
|
| [381] Róbert Gida | 2008-03-27 00:39:19 |
 A.448
AHA, igazad van. Ilyen rossz feladatot régen olvastam. n=1-re biztosan nem igaz: Legyen S="B","C" ez teljesíti a feltételeket, de |S|=2<3, ellentmondás.
Egyébként amit én kb. 5 perc alatt találtam: n>12-re az állítás biztosan igaz! Sőt az alsó korlát ultragyenge. Ok: 1 darab n hosszú S-beli szó 3n darab szót tilt le W-ből, hiszen 1 pozicióra 3 lehetőség van és n pozició van, Így legfeljebb |S|*3n darab szót tudunk letiltani, aminek nagyobb vagy egyenlőnek kell lennie, mint -1+4n, hiszen ennyien vannak az n hosszú szavak, a csupa "A" nélkül. Azaz |S|*3n -1+4n, tehát -1+4n, tehát 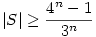 . Ez pedig n>12-re indukcióval belátható, hogy legalább 3*n, ami kellettt, sőt a becslés szerint S-nek exponenciálisan sok eleme van, így a feladat lineáris becslése nudli. . Ez pedig n>12-re indukcióval belátható, hogy legalább 3*n, ami kellettt, sőt a becslés szerint S-nek exponenciálisan sok eleme van, így a feladat lineáris becslése nudli.
|
| Előzmény: [380] kdano, 2008-03-26 21:21:43 |
|
|
| [379] ik68 | 2008-03-26 13:50:06 |
 Ha lenne valakinek egy megoldasa az A.448.-as feladatra, örömmel venném. Köszönöm!
|
|
|
|
| [376] nadorp | 2008-03-21 10:20:26 |
 A.447
A feladat következő általánosítását bizonyítjuk be:
Legyenek a1,...,an tetszőleges valós számok és b1,...,bn tetszőleges pozitív valós számok. Ekkor 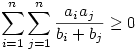 Bizonyítás: Bizonyítás:
Legyen 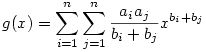 (x (x 0). Azt kell bizonyítani, hogy g(1) 0). Azt kell bizonyítani, hogy g(1) 0 0
Nyilván g(0)=0. Továbbá a függvény deriváltjára
g'(x) 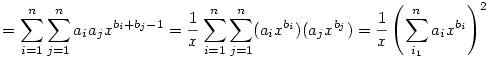
Mivel  >-1 esetén >-1 esetén 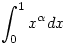 létezik , ezért bi+bj-1>-1 miatt g' integrálható a [0;1] intervallumon és a fentiek miatt g'(x) létezik , ezért bi+bj-1>-1 miatt g' integrálható a [0;1] intervallumon és a fentiek miatt g'(x) 0. Tehát 0. Tehát
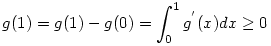 , hiszen nemnegatív függvény integrálja is nemnegatív. , hiszen nemnegatív függvény integrálja is nemnegatív.
|
|
| [375] sakkmath | 2008-03-18 17:16:02 |
 A B. 4056. feladat itt olvasható rapid megoldásával kapcsolatban megjegyzem, hogy létezik tisztán elemi geometriai megoldás is, amely - esetleg - érdekesebb fordulatokat ígér...
|
|
| [374] nadorp | 2008-03-16 11:30:21 |
 A.443
Nevezzük a p kerületű hatszöget H-nak, csúcsai legyenek A,B,C,D,E,F és nevezzük az oldalfelező pontok által meghatározott hatszöget H1-nek az Fi ( i=1...6) csúcsokkal. Húzzuk be az AC,BD,...,FB átlókat. Ezen átlók metszéspontjai H belsejében egy olyan H2 hatszöget határoznak meg, melynek oldalai nyilván párhuzamosak H1 egy-egy oldalával ( melyek középvonalak), tehát H2 szögei szintén 120o-sak. Ebből következik, hogy az AEC és BDF háromszögek minden szöge 60o, tehát ezek a háromszögek szabályosak. Mivel H2 szemközti oldalai nyilván párhuzamosak is, ezért H csúcsait úgy kaphatjuk meg, hogy H2 oldalaira kifelé egy-egy szabályos háromszöget állítunk. Legyenek H2 oldalai a1,...,a6 hosszúak. Ekkor
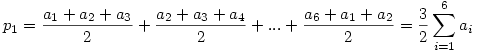 . .
Másrészt 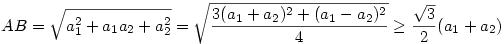
Ha ezt elvégezzük H mindegyik oldalára akkor az kapjuk, hogy
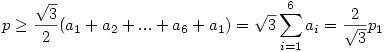
|
 |
|



 (a1,...ak-1), a jobb oldalon pedig
(a1,...ak-1), a jobb oldalon pedig 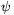 (a1,...ak-1) lesz, ahonnan ak egyértelműen kiszámolható.
(a1,...ak-1) lesz, ahonnan ak egyértelműen kiszámolható. 
 esetén! A jobb oldalon q1(k)(0)
esetén! A jobb oldalon q1(k)(0) k, hiszen indukcióval
k, hiszen indukcióval 



 és G1AD1
és G1AD1



 k=1, így p|a-1
k=1, így p|a-1 
 >-1 esetén
>-1 esetén 
