| [410] rizsesz | 2008-06-17 16:14:37 |
 Az hogy akkor egy feladatra nem érkezett megoldás, az nem tudom, hogy miért nem jelentheti azt, hogy akkoriban a megoldók birtokában nem volt olyan tudásanyag, mint a mai versenyzőkében (és hogy miért kell egyből a lapot bántani megint - ráadásul elképzelésem sincsen, hogy a mai fejeddel, mert ha jól gondolom időközben elvégeztél valamilyen jópofa matek ttk szakot (az a sejtésem, hogy eltét) hogyan tudod megítélni, hogy a mai feladatok könnyebbek. Én egy középszerű dupla B díjazott vagyok, bár, főleg 12.-ben inkább a nehezebb példák mozgattak meg. Egyetem alatt már az A-k is sokkal barátságosabbak lettek.
|
| Előzmény: [408] Róbert Gida, 2008-06-17 00:09:49 |
|
|
| [408] Róbert Gida | 2008-06-17 00:09:49 |
 Valóban szép eredmény tőle. Valószínűleg nyolcadikban egyáltalán nem csináltam Kömalt, már nem emlékszem. De a következő négy évben igen, az N-t pedig 10-ediktől.
Amúgy érdekes is lett volna, ha nyolcadikban 2. lettem volna az N-ban (mostani A-ban) az akkori idősebb szupergeneráció között a Kömalban, csak néhány név, ha mond neked valamit: Pap Gyula, Braun Gábor, Kun Gábor, Gyarmati Katalin, Frenkel Péter, Burcsi Péter, ilyen mezőnyben az első tízbe is lehetetlenség lett volna bekerülni nyolcadikosként, vagy akár kilencedikesként.
Akkori N jelű feladatok pedig lényegesen nehezebbek voltak, mint a mai A jelűek, amellett, hogy akkoriban 4 feladat volt havonként, nem 3. Volt olyan feladat, amire megoldás sem érkezett.
|
| Előzmény: [407] rizsesz, 2008-06-16 22:44:17 |
|
| [407] rizsesz | 2008-06-16 22:44:17 |
 Ja, csak ne felejtsük el a 3. helyezettet, aki most még csak 9. osztályos, fél feladatnyi pontra van lemaradva Lovásztól, és tavaly 8. osztályos korában 2. lett az A-ban. Te is csináltad már 8.-ban az A-t úgy, hogy 2. lettél?
|
| Előzmény: [403] Róbert Gida, 2008-06-14 16:32:33 |
|
|
|
|
| [403] Róbert Gida | 2008-06-14 16:32:33 |
 Kömal A-ban most elég nagy a verseny. Lovász László fia vezet maximális pontszámmal..., csak az A-t csinálja, Kömalban már én is csak ezt csináltam 3.-ban a második félévtől, valahogy untam az F-eket.
|
|
| [402] Káli gúla | 2008-06-13 16:12:29 |
 Egy másik összeszámolási lehetőség a következő: Ha n általános helyzetű átmérőhöz (pólupárhoz) tartozó egyenlítői főkörök a gömb felszínét vn részre osztják, akkor vn+1=vn+2n. Biz.: Válasszuk az n+1-edik főkört (Egyenlítőt), azt a többi n főkör mindegyike egy-egy átellenes pontpárban metszi, ezek nyilván 2n részre osztják az Egyenlítőt. A 2n ív megfelel egy-egy, az Egyenlítő által kettévágott tartománynak, és ez éppen az állított rekurzió. (Tulajdonképpen a fenti indukciós gondolatmenet azt is mutatja, hogy vn nem függ a félkörök helyzetétől.) Az n=1 esetén vn=2, tehát teljes indukcióval vn=n2-n+2.
Tekintsük a pólusokhoz tartozó félgömbök közül azt, amelyik az illető pólust tartalmazza. Ekkor a feldarabolt gömbfelszín egy-egy tartománya pontosan olyan "félgömbrendszer"-hez tartozik, amelyeknek a metszete nem üres. (A metszetnek bármely x pontja a félgömbrendszer pólusaival hegyesszöget zár be, azaz a pólusok egy félgömbön vannak, és fordítva is, ha a pólusok egy x-szel meghatározott félgömbön vannak, akkor a pólusok félgömbjei is mind tartalmazzák x-et.) Azt kaptuk tehát, hogy a gömbi tartományok éppen azokkal a pólusválasztásokkal azonosíthatók, amikor a pólusok egy félgömbön vannak. Különböző "pólusrendszerek" különböző tartományokat állítanak elő, mert legalább egy helyen komplementer félgömbök szerepelnek. Tehát annak a valószínűsége, hogy n pólus ugyanarra a félgömbre esik, 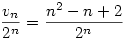 . .
d>2 esetén szó szerint ugyanígy igazolható, hogy az d-dimenziós Sd Rd+1 gömbfelszínen keletkező tartományok vd(n) számára vd(n+1)=vd(n)+vd-1(n) teljesül. Innen a következő általános képletet kaphatjuk: Rd+1 gömbfelszínen keletkező tartományok vd(n) számára vd(n+1)=vd(n)+vd-1(n) teljesül. Innen a következő általános képletet kaphatjuk:
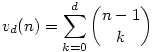
|
| Előzmény: [401] jenei.attila, 2008-06-13 14:02:58 |
|
| [401] jenei.attila | 2008-06-13 14:02:58 |
 Még mindig az A.453-asról néhány gondolat. A feladat tulajdonképpen azt kérdezi, mi a val.-ge annak, hogy a gömbfelületen felvett n db. pont egy félgömbre esik. Az előző hozzászólásomban un jelentette azt, hogy a véletlenszerűen kijelölt n db. minden egyes átmérő valamelyik (de csak egyik) végpontját kiválasztva, hány esetben esnek a pontok egy félgömbre. Erre az
un+1=un+2n
rekurzió adódott, ahol u3=8. Ezt megkaphatjuk egyszerűbben is. Ha n+1 pont egy félgömbre esik, akkor nyilván ezek közül n pont is ugyanarra a félgömbre esik. Ezért un+1-et a következőképpen számoljuk: Ha az egy félgömbre eső n ponthoz hozzávesszük vagy a P, vagy a P' n+1-edik pontot (két egymással átellenes pólus P és P'), akkor biztos, hogy legalább az egyik esetben szintén egy félgömbre esnek a pontok, hiszen a P vagy P' közül legalább az egyik az előző n pont által elfoglalt félgömbre esik. Tehát az ebből adódó kedvező esetek száma un. De előfordulhat, hogy mindkét esetben (akár a P, akár a P' hozzávételével) egy félgömbre esik az n+1 pont (amiből egyet már az előzőekben figyelembe vettünk). Kérdés, hány ilyen eset van. Ez pedig éppen az előző hozzászólásban tárgyalt 2.a) eset, amikoris a maradék n pont egy PP'-őt tartalmazó hosszúsági főkör által határolt egyik félgömbre esik (ez nyilvánvalónak látszik, bár pontosan nem tudom, hogy kéne bizonyítani). Mint láttuk, ez 2n eset (a hosszúsági koordináták egy félkörre esnek). Tehát
un+1=un+2n
Ez alapján a feladat esetleg általánosítható d dimenziós gömbfelületre. Akkor hasonló megfontolásokból
un+1(d)=un(d)+un(d-1)
jönne ki (un(d) jelöli un-et d dimenzióban). 1 dimenzióban (szakasz két végpontja) un(1)=2, hiszen két eset van, amikor vagy az egyik, vagy a másik végpontba kerül az összes pont. 2 dimenzióban (kör kerület) un(2)=2n, mint a 2.a.) pontban láttuk, és a rekurzió is ezt adja... Nyilvánvaló, hogy az általános rekurzió un(d)-re egy d-1 -ed fokú polinomot eredményez, amelynek az értéke n=1 -re 2, n=2 -re 4,...,n=d -re 2d, megfelelően annak, hogy n=1,2,...,d pont, mindig a d dimenziós gömbfelület egyik felére esik. Ezek a kezdőértékek azonban egyértelműen meghatározzák a d-1 -ed fokú polinomot, tehát egyszerű interpolációval könnyen kiszámíthatók. Összefoglalva:

annak a val.-ge, hogy a d dimenziós gömbfelületen véletlenszerűen felvett n pont egy félgömbre esik.
Ezt a hozzászólást vitaindításnak szántam, mert a 2.a.) pontra vonatkozó érvelés számomra sem elég pontos, és a magasabb dimenzióra vonatkozó általánosítást sem látom elég világosan. Minden hozzászólást örömmel veszek.
|
|
| [400] nadorp | 2008-06-13 10:06:14 |
 A.450. Az f:R R függvény kielégíti az R függvény kielégíti az
f(x+f(y))+f(f(x)+y)=2x+2y
függvényegyenletet. Bizonyítsuk be, hogy minden x valós számra f(2x)=2f(x).
Bizonyítás: A függvényegyenletbe behelyettesítve az y=0 illetve x=y értékeket, kapjuk
Bebizonyítjuk, hogy f(0)=0. Ebből már következik a feladat állítása, mert ekkor (1)-ből
f(f(x)+f(f(x)))=f(2x), másrészt (2)-ben elvégezve az x=f(x) helyettesítést
f(f(x)+f(f(x)))=2f(x), azaz
f(2x)=2f(x)
Legyen most már f(0)=b. Ekkor (2)-t véve az x=0 helyen: f(b)=0
(2)-t véve az x=b helyen
f(b+f(b))=2b
f(b)=2b, azaz
2b=0
|
|
| [399] Káli gúla | 2008-06-12 20:27:43 |
 A. 452. Egy 2n csúcsú egyszerű gráfnak n2+1 éle van. Igazoljuk, hogy az élek legalább n háromszöget határoznak meg.
Bizonyítás. Ha n=2, akkor az állítás igaz. Tegyük fel, hogy igaz n-re, és legyen G=(V,E) egy 2n+2 csúcsú gráf n2+2n+2 éllel. Jelöljük  (u)-val az u csúcs fokát és t(G)-vel a G-beli háromszögek számát. Legyen e=(u,v) egy olyan él, amelyre (u)-val az u csúcs fokát és t(G)-vel a G-beli háromszögek számát. Legyen e=(u,v) egy olyan él, amelyre  (u)+ (u)+ (v)-1 minimális, és legyen a minimum értéke m. (v)-1 minimális, és legyen a minimum értéke m.
(1) Ha m>2n+1, akkor u-nak és v-nek van közös szomszédja, vagyis e egy háromszögben van, és ugyanez igaz az összes többi élre is, hisz azok végpontjaiból is együtt legalább m él indul. Tehát G minden éle benne van egy háromszögben, ezért 3t(G) n2+2n+2>3(n+1). n2+2n+2>3(n+1).
(2) Ha m=2n+1, akkor az u, v csúcsokat és a belőlük induló 2n+1 élt elhagyva egy 2n csúcsú G1 gráfot kapunk, amelyben n2+1 él marad, így az indukciós feltevés szerint t(G1) n. Még egy háromszöget tudunk G-ben találni, vagy úgy, ha (I) akár az u, akár a v szomszédai között megy él (így u ill. v csúcsú háromszöget kapunk), vagy úgy, ha (II) u-nak és v-nek van közös szomszédja (így u, v és a közös szomszéd alkot háromszöget). E két lehetőség egyikének be kell következni, különben az u és a v csúcs szomszédai a G1 gráf csúcsainak két színnel színezését adnák, vagyis G1 páros gráf volna, ellentétben azzal, hogy t(G1) n. Még egy háromszöget tudunk G-ben találni, vagy úgy, ha (I) akár az u, akár a v szomszédai között megy él (így u ill. v csúcsú háromszöget kapunk), vagy úgy, ha (II) u-nak és v-nek van közös szomszédja (így u, v és a közös szomszéd alkot háromszöget). E két lehetőség egyikének be kell következni, különben az u és a v csúcs szomszédai a G1 gráf csúcsainak két színnel színezését adnák, vagyis G1 páros gráf volna, ellentétben azzal, hogy t(G1) n. n.
(3) Ha m<2n+1, akkor az u, v csúcsokat és a belőlük induló m élt elhagyva a kapott G1 gráfban most legalább n2+2 él marad. Vegyünk G1-ben az indukciós feltevés szerint létező háromszöget, és töröljük az egyik élét. Tudjuk, hogy a megmaradt n2+1 él is legalább n háromszöget határoz meg. Visszahúzva a törölt élt, megkapjuk az n+1-edik háromszöget.
|
|
| [398] Káli gúla | 2008-06-12 20:25:55 |
 A. 454. Létezik-e olyan konstanstól különböző valós együtthatós p polinom, amelyre minden x valós szám esetén p2(x)-1=p(x2+1) teljesül?
Nem létezik. (1) Először lássuk be, hogy minden n>0 esetén pontosan egy n-edfokú p(x) polinom létezik, amelyre 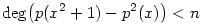 . Bizonyítás. Ilyen p polinom csak a főtaggal azonos paritású x hatványokat tartalmazhat, egyébként p2(x)-ben n-nél nem kisebb páratlan kitevős tag is adódna, ami . Bizonyítás. Ilyen p polinom csak a főtaggal azonos paritású x hatványokat tartalmazhat, egyébként p2(x)-ben n-nél nem kisebb páratlan kitevős tag is adódna, ami 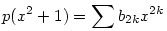 miatt lehetetlen. Legyen miatt lehetetlen. Legyen 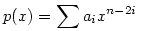 , ekkor a követelmény szerint: , ekkor a követelmény szerint:
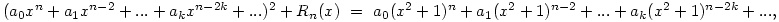
ahol Rn(x) foka kisebb, mint n. Innen az a0, a1, . . . értékeket egymás után megkaphatjuk, ha az x2n, x2n-2 . . . együtthatóit a két oldalon összehasonlítjuk. Így a0=1, 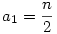 , , 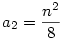 , , 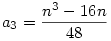 . . . Általában, ha i<k indexekre már ismerjük az ai értékeket, akkor az x2n-2k együtthatója a bal oldalon 2ak+ . . . Általában, ha i<k indexekre már ismerjük az ai értékeket, akkor az x2n-2k együtthatója a bal oldalon 2ak+ (a1,...ak-1), a jobb oldalon pedig (a1,...ak-1), a jobb oldalon pedig  (a1,...ak-1) lesz, ahonnan ak egyértelműen kiszámolható. (a1,...ak-1) lesz, ahonnan ak egyértelműen kiszámolható.
(2) Jelöljük a fentiek miatt egyértelműen meghatározott n-edfokú polinomot Hn-nel, a maradékát Rn-nel, azaz legyen 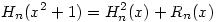 , ahol deg Rn<n. Ekkor , ahol deg Rn<n. Ekkor 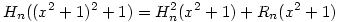 is teljesül, azaz H2n, R2n egyértelműsége és is teljesül, azaz H2n, R2n egyértelműsége és 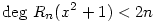 miatt azt kapjuk, hogy miatt azt kapjuk, hogy 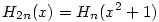 és és 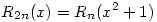 . Tehát a kiinduló állítást elég páratlan fokú p polinomokra igazolni, hiszen . Tehát a kiinduló állítást elég páratlan fokú p polinomokra igazolni, hiszen 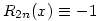 -ből -ből 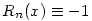 is következne. is következne.
(3) Indirekt tegyük fel, hogy p(x) páratlan fokú és teljesül rá a 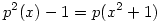 azonosság. Írjuk át ezt a azonosság. Írjuk át ezt a 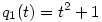 és és 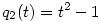 jelölésekkel jelölésekkel 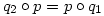 alakba. Teljes indukcióval (a q-kat egymás után "áthúzva" p-n) azonnal adódik, hogy alakba. Teljes indukcióval (a q-kat egymás után "áthúzva" p-n) azonnal adódik, hogy
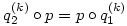
Vizsgáljuk a két oldalt az x=0 helyen k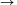 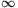 esetén! A jobb oldalon q1(k)(0) esetén! A jobb oldalon q1(k)(0) k, hiszen indukcióval k, hiszen indukcióval ![\matrix{}q_1^{(k+1)}(0)=\big[q_1^{(k)}(0)\big]^2+1 \ge k+1](keplet.cgi?k=A8861E60FE13FFE2) , ezért , ezért 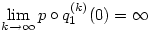 . A bizonyítás elején tett megjegyzés szerint p(0)=0, mert p minden tagja páratlan fokú, ezért a bal oldal x=0-ban egy kettő hosszúságú ciklusba van zárva, vagy 0, vagy -1, mert . A bizonyítás elején tett megjegyzés szerint p(0)=0, mert p minden tagja páratlan fokú, ezért a bal oldal x=0-ban egy kettő hosszúságú ciklusba van zárva, vagy 0, vagy -1, mert 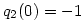 és és 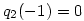 . Ez az ellentmondás igazolja az állítást. . Ez az ellentmondás igazolja az állítást.
Megjegyzés. Ugyanígy látható be, hogy a 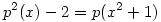 azonosság sem teljesülhet semmilyen p polinomra, csak ekkor az utolsó képlet bal oldalán a q2(t)=t2-2 polinom iteráltjai nem oszcillálnak, hanem azonosan 2 értékűek a 0 helyen, de ez is lehetetlen végtelenbe tartó jobb oldal mellett. azonosság sem teljesülhet semmilyen p polinomra, csak ekkor az utolsó képlet bal oldalán a q2(t)=t2-2 polinom iteráltjai nem oszcillálnak, hanem azonosan 2 értékűek a 0 helyen, de ez is lehetetlen végtelenbe tartó jobb oldal mellett.
|
|
| [397] jenei.attila | 2008-06-12 10:29:26 |
 Az előzőhöz javítás: "Figyelembe véve, hogy tn=0, azaz un=8" helyesen: Figyelembe véve, hogy t3=0, azaz u3=8.
A 2.a.) ponthoz kiegészítés: itt azt állítom, hogy a PP' átmérő pontosan akkor döfi át a maradék n pont által meghatározott konvex burkot, ha az n pont husszúsági koordinátáiból az egyenlítő mentén képződő n oldalú sokszög tartalmazza a gömb középpontját. Elég ezt belátni n=3 esetén, ugyanis ha PP' átdöfi a burkot, akkor az n pontból kiválasztható 3, amelyek által alkotott háromszöglemezt szintén átdöf. Fordítva, ha ilyen háromszöhlemezt átdöf, akkor a burkot is. Mindez a konvex burok tulajdonsága miatt van így. Ha pedig egy háromszög lemezt átdöf az átmérő, akkor nyilván a három pont hosszúsági koordinátáiból az egyenlítő mentén képződő háromszög tartalmazza a gömb középpontját. Ez esetben maga az egyenlítő mentén keletkező n szög is tartalmazza a gömb középpontját. Továbbá az is világos, hogy a szóbanforgó 3 ponthoz hozzávéve vagy a P, vagy a P' pontot, a keletkező tetraéderek pontosan egyike fogja tartalmazni a gömb középpontját, hiszen a három pontból, és a P és P'-ből álló 5 pontú konvex burok teljes egészében tartalmazza a PP' átmérőt (és ezzel együtt a gömb kp.-ját is).
|
|
| [396] jenei.attila | 2008-06-11 22:32:35 |
 Az A.453 feladatra írok egy megoldást. A gömbfelületen egymástól függetlenül véletlenszerűen kiválasztunk n pontot. Mi a val.-ge, hogy a kiválasztott pontok konvex burka tartalmazza a gömb középpontját?
Megoldás: Válasszuk ki a pontokat a következőképpen. Először adjunk meg n véletlenszerűen választott átmérőt. Egy átmérő a gömbfelületet két pontban döfi, amelyek egyikét választjuk pontként. Így az átmérők kijelölése után 2n lehetőség van a pontok kiválasztására. Össze fogjuk számolni, hogy a 2n lehetőségből hány olyan van, amikor a kiválasztott pontok konvex burka tartalmazza a gömb középpontját (mint látni fogjuk, ez független az átmérők helyzetétől). Jelöljük ezt tn-nel, ekkor a keresett val.-ég 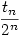 . tn+1-re egy rekurzív összefüggést adunk meg. Jelöljük ki az egyik átmérőt (PP'), és vizsgáljuk ennek, valamint a maradék n pont által meghatározott konvex buroknak a helyzetét. Három esetet különböztetünk meg: . tn+1-re egy rekurzív összefüggést adunk meg. Jelöljük ki az egyik átmérőt (PP'), és vizsgáljuk ennek, valamint a maradék n pont által meghatározott konvex buroknak a helyzetét. Három esetet különböztetünk meg:
1.) A maradék n pont konvex burka tartalmazza a gömb középpontját.
2.a.) A maradék n pont konvex burka nem tartalmazza a gömb középpontját, és nincs közös pontja a PP' átmérővel.
2.b.) A maradék n pont konvex burka nem tartalmazza a gömb középpontját, de a PP' átmérő döfi a burkot.
Az 1.) esetben akár a P, akár a P' potot választjuk a már kiválasztott n pont mellé, az új konvex burok szintén tartalmazni fogja a gömb kp.-ját. Tehát az ebből adódó kedvező esetek száma 2tn.
A 2.a.) eset akkor állhat fenn, ha a maradék n pont "hosszúsági koordinátáiból" az egyenlítő mentén keletkező n oldalú sokszög nem tartalmazza a gömb kp.-ját (PP'-őt tekintjük forgástengelynek, az erre merőleges főkör az egyenlítő). Tehát meg kell oldani az analóg síkbeli feladatot: a körben véletlenszerűen kiválasztva n átmérőt, majd az egyes átmérők egyik végpontját kijelölve, hány esetben nem fogja tartalmazni a kör kp.-ját a kijelölt pontokból álló n oldalú sokszög (vagyis mikor esnek egy félkörre)? Erre a válasz 2n, ami könnyen belátható. Tehát a 2.a.) pontnak megfelelő esetek száma 2n. Ezen esetekben a P vagy P' hozzávételekor keletkező konvex burok sem tatalmazza a gömb kp.-ját.
A 2.b.) esetek száma nyilván az összes esetek száma - 1.)esetek száma - 2.a.) esetek száma, vagyis 2n-tn-2n. A 2.b.) esetben, azonban a P vagy P' (kizáró vagy) hozzávételével a keletkező konvex burok tartalmazni fogja a gömb kp.-ját, hiszen PP' átdöfi a maradék konvex burkot. Tehát az összes kedvező esetek száma:
tn+1=2tn+2n-tn-2n=2n+tn-2n
. Ezzel a feladat tulajdonképpen meg van oldva, már csak a tn-re adunk egy zárt képletet. Legyen un:=2n-tn, vagyis azon esetek száma, amikor a konvex burok nem tartalmazza a gömb kp.-ját. Tehát
un+1=2n+1-tn+1=2n-tn+2n=un+2n
Figyelembe véve, hogy tn=0, azaz un=8, kapjuk, hogy
un=n2-n+2
. Vagyis a feladatra a válasz:
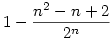
annak a valószínűsége, hogy a gömb kp-ja benne lesz a véletlenszerűen választott n pont által meghatározott konvex burokban.
|
|
|
| [394] Sirpi | 2008-05-26 08:35:33 |
 Ha gondolkodtál volna kicsit, mielőtt megint fröcsögsz, akkor rájöttél volna, hogy a feladat nincs elszúrva. Senki nem mondta, hogy minden N-re kell lennie ilyen színezésnek. Ha nincs, akkor arra az N-re az állítás üres. A stílusod viszont nem nagyon fejlődik...
|
| Előzmény: [393] Róbert Gida, 2008-05-26 00:58:52 |
|
| [393] Róbert Gida | 2008-05-26 00:58:52 |
 "A.448. helyett új példát tűztek ki."
No igen. De ezt is sikerült elszúrniuk: "A. 448. Az 1,2,...,N számokat kiszíneztük 3 színnel úgy, hogy mindegyik szín legfeljebb 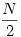 -ször szerepel." -ször szerepel."
N=1-re egy lehetséges színezést azért megnéznék...
|
| Előzmény: [389] Róbert Gida, 2008-05-08 16:58:43 |
|
| [392] Python | 2008-05-18 17:56:28 |
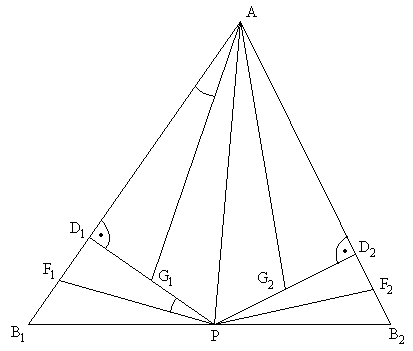
 Legyen PD1 felezőpontja G1, PD2 felezőpontja G2! Mivel A felezi PQ-t, AG1 középvonal PQD1 hároszögben, így AG1 párhuzamos QD1-el. Hasonlóan AG2 párhuzamos QD2-vel.
Tegyük fel, hogy QD1-merőleges PF1-re! Ekkor AG1 is merőleges PF1-re. Mivel PD1 merőleges AD1-re, így F1PD1 és G1AD1 és G1AD1 szögek megegyeznek (merőleges szárú szögek). Így F1PD1 és G1AD1 háromszögek hasonlóak, mivel a szögeik megegyeznek. Így szögek megegyeznek (merőleges szárú szögek). Így F1PD1 és G1AD1 háromszögek hasonlóak, mivel a szögeik megegyeznek. Így 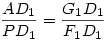 , de így, mivel PD1=2G1D1 és D1B1=2F1D1, , de így, mivel PD1=2G1D1 és D1B1=2F1D1, 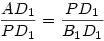 , ami azt jelenti, hogy AD1P és PD1B1 derékszögű háromszögek is hasonlóak. Így pl. D1PB1 , ami azt jelenti, hogy AD1P és PD1B1 derékszögű háromszögek is hasonlóak. Így pl. D1PB1 =D1AP =D1AP =90o-D1PA =90o-D1PA , és emiatt B1PA , és emiatt B1PA =90o, ami azt jelenti, hogy AP a háromszög A-ból induló magassága, P a magasságtalppont B1B2-n (mivel a háromszög hegyesszögű, ez B1B2 szakaszon van). =90o, ami azt jelenti, hogy AP a háromszög A-ból induló magassága, P a magasságtalppont B1B2-n (mivel a háromszög hegyesszögű, ez B1B2 szakaszon van).
Innen visszfelé ugyanez elmondható a másik oldalon, ami miatt teljesül a feladat állítása. (APB2 =90o, így AD2P és PD2B2 hasonló, mivel PAD2 =90o, így AD2P és PD2B2 hasonló, mivel PAD2 =90o-APD2 =90o-APD2 =D2PB2 =D2PB2 , így AD2G2 és PD2F2 is hasonló ( , így AD2G2 és PD2F2 is hasonló (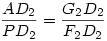 miatt), de ekkor G2AD2 miatt), de ekkor G2AD2 =F2PD2 =F2PD2 , és ebből, valamint PD2 és AD2 merőlegességéből következik, hogy AG2 merőleges PF2-re, így QD2 merőleges PF2-re, és ezt kellett igazolni.) , és ebből, valamint PD2 és AD2 merőlegességéből következik, hogy AG2 merőleges PF2-re, így QD2 merőleges PF2-re, és ezt kellett igazolni.)
A lényeg az, hogy ha van két hasonló háromszögünk, és mindkettőt "félbevágjuk" egymásnak megfelelő csúcsaikból induló súlyvonalakkal, akkor a megfelelő részháromszögek is hasonlóak lesznek. Ezt itt csak derékszögű háromszögekre igazoltam és használtam fel.
|
 |
| Előzmény: [390] S.Ákos, 2008-05-17 09:21:05 |
|
|
| [390] S.Ákos | 2008-05-17 09:21:05 |
 Valaki tudna mutatni egy elemi geometriai megoldást a B.4088-as feladatra?
|
|
|
| [388] rizsesz | 2008-04-16 14:22:44 |
 Nagyon szép megoldás, kedves Ákos (bár eléggé adta magát a kis Fermat-tétel :)).
Néhány gondolat amúgy eszembe jutott a kitűzött K problémákkal kapcsolatban.
A K. 167. ugyanabba a hibába esik, mint a K. 90.
Azt kérte ott ugyanis a feladat, hogy adjunk meg minél több megoldást, míg maximális pont arra járt, ha igazoltad, hogy két megoldás van és nincsen több. Érdemes lenne ezt a javítóknak most is figyelembe venni, és ilyen hibába nem beleesni újra.
A másik a K. 168. Ennek második része pedig már korábban tárgyalt B feladat (azt hiszem 2002 - 2003 májusi). Ez persze nem először fordul elő, de úgy gondolom, hogy ilyenekre érdemes lenne ügyelni.
Üdv, rizs
|
|
|
|





 és
és  szöge, amelyekre 2
szöge, amelyekre 2

 Rd+1 gömbfelszínen keletkező tartományok vd(n) számára vd(n+1)=vd(n)+vd-1(n) teljesül. Innen a következő általános képletet kaphatjuk:
Rd+1 gömbfelszínen keletkező tartományok vd(n) számára vd(n+1)=vd(n)+vd-1(n) teljesül. Innen a következő általános képletet kaphatjuk:  R függvény kielégíti az
R függvény kielégíti az  (u)-val az u csúcs fokát és t(G)-vel a G-beli háromszögek számát. Legyen e=(u,v) egy olyan él, amelyre
(u)-val az u csúcs fokát és t(G)-vel a G-beli háromszögek számát. Legyen e=(u,v) egy olyan él, amelyre  n2+2n+2>3(n+1).
n2+2n+2>3(n+1).  (a1,...ak-1), a jobb oldalon pedig
(a1,...ak-1), a jobb oldalon pedig 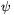 (a1,...ak-1) lesz, ahonnan ak egyértelműen kiszámolható.
(a1,...ak-1) lesz, ahonnan ak egyértelműen kiszámolható. 
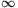 esetén! A jobb oldalon q1(k)(0)
esetén! A jobb oldalon q1(k)(0)

 és G1AD1
és G1AD1



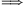 k=1, így p|a-1
k=1, így p|a-1