|
|
| [493] Csimby | 2009-11-26 15:09:51 |
 Ellenpélda: legyen b=6 és p=7.
b2 1 (mod p) nagyon-nagyon-nagyon nem csak p=3 esetén teljesül. 1 (mod p) nagyon-nagyon-nagyon nem csak p=3 esetén teljesül.
A modulo p maradékosztályok a 0-t kivéve a szorzásra nézve p-1 rendű csoportot alkotnak. És csak annyit állíthatunk, hogy minden elem rendje osztja a csoport rendjét. Tehát b2 1(mod p)-ből csak az következik, hogy p páratlan. 1(mod p)-ből csak az következik, hogy p páratlan.
|
| Előzmény: [492] bily71, 2009-11-26 09:57:26 |
|
|
| [491] bily71 | 2009-11-26 09:46:20 |
 És most jöjjön egy másik lehetséges megoldás a B.4026. feladatra:
Minden p>3 prim felírható p=6k 1alakban. 1alakban.
A binomiális tétel értelmében
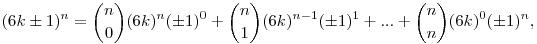
ahol a jobb oldali összeg utolsó tagja
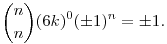
Mivel az összeg minden tagja az utolsó kivételével osztható 6-tal, ezért
(6k )n )n  1(mod 6). 1(mod 6).
Tételezzük fel indirekt módón, hogy a
pk+pm=a2
egyenlőség teljesül, ahol a pozitív egész, mivel négyzetszámon egy egész szám második hatványát értjük.
1. eset: 0<k m, és k és m paritása megegyezik. Ebben az esetben m, és k és m paritása megegyezik. Ebben az esetben
a2  2(mod 6), 2(mod 6),
de ez csak úgy lehetséges, ha az
a2  2(mod 3) 2(mod 3)
kongruencia is teljesül. Ez pedig nem teljesülhet, mert az Euler-Fermat-tétel miatt
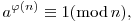
ha a és n relatív prímek, és mivel  (3)=2, ezért, ha 3 (3)=2, ezért, ha 3|a, akkor a2 1(mod 3), ha pedig 3|a, akkor a2 1(mod 3), ha pedig 3|a, akkor a2 0(mod 3), így az a2 0(mod 3), így az a2  2(mod 3) kongruencia nem teljesülhet. 2(mod 3) kongruencia nem teljesülhet.
2. eset: 0<k<m, és k és m paritása ellentétes. Ekkor
pk+pm=pm(pk-m+1)
pm(pk-m+1)=a2,
ez csak úgy lehetséges, ha 2|m. Osszunk le pm-mel, legyen 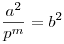 , és k-m=x, ekkor , és k-m=x, ekkor
px+1=b2.
Mivel px  1(mod 3), ezért vagy a b2 1(mod 3), ezért vagy a b2 2(mod 3), vagy a b2 2(mod 3), vagy a b2 0(mod 3) kongruencia teljesül. Az előbbi nem teljesülhet az 1.-ben tárgyaltak miatt. Nézzük az utóbbit: 0(mod 3) kongruencia teljesül. Az előbbi nem teljesülhet az 1.-ben tárgyaltak miatt. Nézzük az utóbbit:
px+1 1(mod p), 1(mod p),
ebből következik, hogy
b2 1(mod p). 1(mod p).
Ez viszont azt jelentené, mivel az Euler-Ferma-tétel megfordítása is igaz, hogy p=3, vagy 3|p, de egyik sem lehetséges, mert a feladat szerint p>3 és p P, azaz prím. P, azaz prím.
3. eset: k=m=0, ekkor a2 2(mod 3), mivel pk=pm=1, de ez a kongruencia nem teljesülhet az 1.-ben részletezett okok miatt. Több lehetőség nincs. 2(mod 3), mivel pk=pm=1, de ez a kongruencia nem teljesülhet az 1.-ben részletezett okok miatt. Több lehetőség nincs.
|
|
| [490] R.R King | 2009-11-24 18:42:27 |
 Szerintem nem kell aggódnod, mert már most többet tudsz, mint a felvételizők többsége:) Hidd el sokat változott a színvonal 20 év alatt. A másik topicban tett hibás gondolatmeneteidről meg annyit, hogy ki tudja, talán egyszer valaki hasonló nyomon indulva bizonyít be valamit a láncszemeket megfelelően helyretéve.. Vajon hány tétel született úgy, hogy előtte 100 rossz utat végigjárt a megoldó??? A legtöbben pedig, akik bírálnak 2-3 matektanártól tanulták amit tudnak, önállóan még nem sokat tettek le az asztalra..Akinek nem inge, ne vegye magára.
|
| Előzmény: [489] bily71, 2009-11-24 17:52:53 |
|
| [489] bily71 | 2009-11-24 17:52:53 |
 Nemcsak szerencsésebb, hanem helyesebb is. Amit én írtam, csak k=2 esetén lehet igaz. Hirtelen nem is jutott eszembe, hogy k bármilyen egész lehet, annyira a négyzetszámokra koncentráltam. Azt hiszem, nem lesz egyszerű visszaülni 20 év után az iskolapadba, egy kicsit össze kell szednem magam, hogy sikerüljön a felvételi:)
|
| Előzmény: [488] R.R King, 2009-11-24 16:46:04 |
|
| [488] R.R King | 2009-11-24 16:46:04 |
 A 3. rész végén talán szerencsésebb azt mondani, egy prímhatvány csak úgy bontható egészek szorzatára, ha a tényezők maguk is ugyanannak a prímnek a hatványai. Jelen esetben a a+1 és a-1 különbsége 2, így ezek nem lehetnek, mert p>3, még az sem lehet hogy az egyik tényező 1 a másik pedig maga p a k-on(leellenőrizhető!)
|
| Előzmény: [487] bily71, 2009-11-24 16:00:25 |
|
| [487] bily71 | 2009-11-24 16:00:25 |
 Sokan bírálták (jogosan) eddigi működésemet, ezért jöjjön egy lehetséges megoldás egy, a tudásszintemhez méretezett feladatra:
B.4026. Legyen p>3 prímszám, k és m pedig nemnegatív egész számok. Igazoljuk, hogy pk+pm nem lehet négyzetszám.
Megoldás:
pk+pm=a2, ahol a nemnegatív egész, ugyanis négyzetszám definició szerint csak egy egész szám második hatványa lehet. Négy eset lehetséges:
1. k=m=0, ekkor
pk=pm=1
pk+pm=2
2=a2
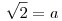 , ,
ami nem lehet, mert a a feladat szerint egész.
2. k=m>0, ekkor
pk=pm
pk+pm=2pm
2pm=a2,
ami nem lehet, mert egy négyzetszám prímtényezős felbontásában minden hatványkitevő páros, a baloldali 2-es kitevője pedig páratlan.
3. k>m=0, ekkor
pm=1
pk+pm=pk+1
pk+1=a2
pk=a2-1
pk=(a+1)(a-1),
ami nem lehet, mert (a+1) (a-1), és egy prímhatvány szorzótényezős felbontásában nem szerepelhet két különböző szám. (a-1), és egy prímhatvány szorzótényezős felbontásában nem szerepelhet két különböző szám.
4. k>m>0, ekkor
pk+pm=pm(pk-m+1)
pm(pk-m+1)=a2,
ami csak úgy lehetséges, ha 2|m, osszuk le az egyenletet pm-el. Legyen 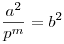 , és k-m=x, b és x nemnegatív egészek, ekkor , és k-m=x, b és x nemnegatív egészek, ekkor
px+1=b2
px=b2-1
px=(b+1)(b-1),
ez pedig nem lehet a 3. esetnél részletezett okok miatt. Több lehetőség nincs.
|
|
|
|
|
| [483] m2mm | 2009-11-11 14:24:35 |
 B. 4211. Mutassuk meg, hogy nincs olyan racionális együtthatós polinom, amely pontosan egy egész helyen vesz fel nem egész értéket. Létezik-e ilyen tulajdonságú valós együtthatós polinom?
Megoldás: Mint ismert, ha egy p(x) valós együtthatós polinom k-adfokú, akkor tetszőleges valós a-ra 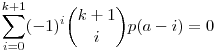 . .
Ha véges sok a-ra lesz p(a) nem egész(p foka k), akkor vegyük a legkisebbet, mondjuk b-t. Ekkor 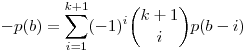 . A bal oldal nem egész, a jobb viszont igen:ellentmondás, nem létezik ilyen val. együtthatós polinom. . A bal oldal nem egész, a jobb viszont igen:ellentmondás, nem létezik ilyen val. együtthatós polinom.
|
|
| [482] nadorp | 2009-10-20 16:18:08 |
 Az biztos, hogy az állítás n=2 esetén nem mindig igaz. Pontosabban:
1.)  esetén a maximum valóban esetén a maximum valóban 
2.minden más k-ra a maximum 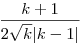
Szerint n>2 esetén is valami hasonló lesz a helyzet. Nem számoltam még végig, de szerintem az ai-k legfeljebb 2-féle értéket vehetnek fel maximum esetén, pontosabban bizonyos k esetén az összes egyenlő, a másik esetben pedig két különböző érték
|
| Előzmény: [481] m2mm, 2009-10-19 21:01:55 |
|
| [481] m2mm | 2009-10-19 21:01:55 |
 Üdv! Talált valaki a B. 4201.-re olyan megoldást, ami alkalmazható ai>0, i=1,2,...n (an+1=a1)és adott k>0 esetén
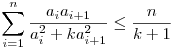 bizonyítására(ha ez igaz)? bizonyítására(ha ez igaz)?
|
|
| [480] Tibixe | 2009-10-13 21:39:44 |
 Lényegesen egyszerűbb nem hiszem hogy lenne.
A te 2. lemmádból szerintem elég sokféleképpen be lehet fejezni, de hallottam azt elkerülő megoldásról is.
A. 487. meglett neked?
|
| Előzmény: [479] S.Ákos, 2009-10-13 19:45:59 |
|
| [479] S.Ákos | 2009-10-13 19:45:59 |
 A. 486. Eléggé vázlatosan:
Lemma1: 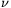 (2n)- (2n)-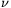 (n)=n. Egyszerű teljes indukció n-re (n)=n. Egyszerű teljes indukció n-re
Lemma2.: 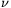 (n)+ (n)+ (n)=n, ahol (n)=n, ahol  (n) az 1-esek száma n 2-es számrendszerbeli alakjában. Itt felhasználjuk az első segédtételt, és azt, hogy (n) az 1-esek száma n 2-es számrendszerbeli alakjában. Itt felhasználjuk az első segédtételt, és azt, hogy  (2n+1)= (2n+1)= (n)+1; (n)+1;  (2n)= (2n)= (n), teljes indukcióval. (n), teljes indukcióval.
Lemma3.: Minden n-re van végtelen sok olyan a1<a2<a3<... egész szám, hogy (2ai-1,n)=1, és 2a1-1 2a2-1 2a2-1 ...(modn). ...(modn).  , k páratlan. Legyen q olyan prím, amire q>Max(opi(2),s). Ezzel a választással pi|2q-1 nem állhat a rend tulajdonságai miatt, 2-vel nem osztható. Másrészt , k páratlan. Legyen q olyan prím, amire q>Max(opi(2),s). Ezzel a választással pi|2q-1 nem állhat a rend tulajdonságai miatt, 2-vel nem osztható. Másrészt 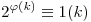 , így q+l , így q+l (k) alakú számok megfelelnek, ai:=q+i (k) alakú számok megfelelnek, ai:=q+i (k) (k)
Megmutatjuk, hogy a következő számok: A1=2a1,A2=2a1+2a2,...,Am=2a1+2a2+...+2am teljes maradékrendszer mod m. Az Ai szám 2-es számrendszerbeli felírásában i darab 1-es van, így a 2-ik lemma alapján:  m). De (2a1-1,m)=1, így ez az m szám teljes maradékrendszert alkot mod m m). De (2a1-1,m)=1, így ez az m szám teljes maradékrendszert alkot mod m
Valaki tud mutatni egyszerűbbet?
|
|
| [478] rizsesz | 2009-05-21 14:49:20 |
 Annak idején amúgy lényegesen több jó megoldás volt :) Nem mellesleg az ottani megoldás tartalmazza a diszkussziót: http://www.komal.hu/verseny/2002-01/B.h.shtml (a legutolsó mondat, persze azt ki kell fejteni).
|
| Előzmény: [477] m2mm, 2009-05-21 14:44:22 |
|
| [477] m2mm | 2009-05-21 14:44:22 |
 Hát igen. A 3 pontosok többsége, de nem mindenki megtalálta, ezt kaptam:
Javító (az összes versenyzőnek), 2009/05/09 19:36
Kedves Versenyzők!
A feladat lényegében egyezik a B.3521. korábbi feladattal, de ott sajnálatos módon rossz megoldás szerepel, mely csupán 3 pontot ér. Ha észrevettétek, hogy 1 vagy 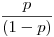 a jó valószínűség, az még bizonyításra szorul, hogy a jó valószínűség, az még bizonyításra szorul, hogy  esetén esetén 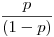 lesz a jó megoldás, ez folytonossággal, határértékszámítással vagy teljes indukcióval könnyen igazolható. lesz a jó megoldás, ez folytonossággal, határértékszámítással vagy teljes indukcióval könnyen igazolható.
Egy további probléma: aki ezt a levelet megkapta, az feltehetően megnézte, márcsak kíváncsiságból is azt a B.3521.-es feladatot.
A fölötte levő B. 3515. feladat:
Bizonyítsuk be, hogy a ![\big[\sqrt2\cdot n\big]](keplet.cgi?k=E20B2A2575100ADE) alakú számok között végtelen sok 2-hatvány van. (4 pont) alakú számok között végtelen sok 2-hatvány van. (4 pont)
Magyarán az 5 pontos áprilisi feladatra lesz pár másolt megoldás, mivel ehhez hasonlóan meg lehet oldani (lehet hogy kicsit nehezebb a mostani, de a módszer ugyanaz). Úgy gondolom, a javítóknak erre vigyázni kéne.
|
| Előzmény: [476] rizsesz, 2009-05-21 11:22:34 |
|
| [476] rizsesz | 2009-05-21 11:22:34 |
 A baktériumos b-t meg már kitűzték annak idején a B-ben (2002 januárjában :))
|
|
| [475] rizsesz | 2009-05-21 11:22:06 |
 C. 976. Adjuk meg azt a legszűkebb intervallumot, ahová három pozitív szám összegének és a reciprokaik összegének szorzata eshet.
Itt amúgy nem szükséges annak bizonyítása, hogy bármilyen értékhez van megfelelő a, b, c hármas?
|
|
| [474] Blinki Bill | 2009-05-19 20:54:27 |
 Az A.479. megoldásában nem úgy van helyesen, hogy "...és (3) csak d>6 esetén teljesülhet..."?
|
|
| [473] Tibixe | 2009-05-18 19:02:23 |
 A480-at hogy kellett volna megoldani? Kinek sikerült?
|
|
|
|




 1 (mod p) nagyon-nagyon-nagyon nem csak p=3 esetén teljesül.
1 (mod p) nagyon-nagyon-nagyon nem csak p=3 esetén teljesül.  1alakban.
1alakban.  m, és k és m paritása megegyezik. Ebben az esetben
m, és k és m paritása megegyezik. Ebben az esetben  (3)=2, ezért, ha 3
(3)=2, ezért, ha 3 P, azaz prím.
P, azaz prím. 
 (a-1), és egy prímhatvány szorzótényezős felbontásában nem szerepelhet két különböző szám.
(a-1), és egy prímhatvány szorzótényezős felbontásában nem szerepelhet két különböző szám. 

 (2n)-
(2n)- (n)=n, ahol
(n)=n, ahol 