| [552] HoA | 2010-05-13 16:27:19 |
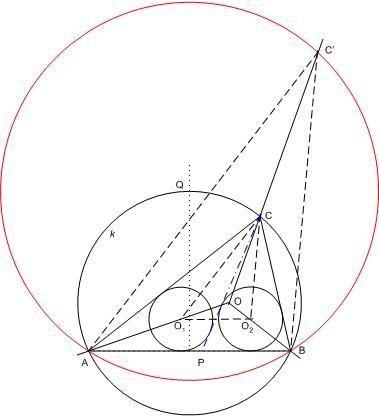
 B.4269 megoldása „A KöMaL pontverseny” témában leírtak kapcsán. Tekinsük a feladatot megoldottnak. Legyen ABC körülírt köre k, beírt körének középpontja O . Az APC és BCP háromszögek beírt k1 , k2 köreinek középpontja O1 ill. O2 . Mivel ezek a körök ABC körülírt köre k, beírt körének középpontja O . Az APC és BCP háromszögek beírt k1 , k2 köreinek középpontja O1 ill. O2 . Mivel ezek a körök ABC 2-2 oldalát érintik, O1 ill. O2 rajta vannak az AO ill. BO szögfelezőkön. A körsugarak egyenlősége miatt O1O2 párhuzamos AB -vel. Ugyancsak az érintés miatt O1C felezi az ACP , O2C a BCP szöget. O1O2C 2-2 oldalát érintik, O1 ill. O2 rajta vannak az AO ill. BO szögfelezőkön. A körsugarak egyenlősége miatt O1O2 párhuzamos AB -vel. Ugyancsak az érintés miatt O1C felezi az ACP , O2C a BCP szöget. O1O2C C-nél levő szöge ezért C-nél levő szöge ezért  /2 . Nagyítsuk az O középpontból az O1O2C /2 . Nagyítsuk az O középpontból az O1O2C -et úgy, hogy O1 képe A legyen. Ekkor a párhuzamosság miatt O2 képe B lesz. A C pont C’ képe egyrészt rajta van az OC egyenesen, másrészt az AB szakasz -et úgy, hogy O1 képe A legyen. Ekkor a párhuzamosság miatt O2 képe B lesz. A C pont C’ képe egyrészt rajta van az OC egyenesen, másrészt az AB szakasz  /2 látőszögű, C oldali körívén. /2 látőszögű, C oldali körívén.
A szerkesztés menete: Rajzoljuk meg az AB szakasz  /2 látószögű körívét a C -t tartalmazó oldalon. Ennek a CO egyenessel alkotott metszéspontja C’ .Húzzunk párhuzamost C-n keresztül AC’ -vel, metszéspontja AO -val legyen O1, valamint C-n keresztül BC’ -vel, metszéspontja BO -val legyen O2. Az O1 középpontú, AB -t érintő kör C -ből húzott, AC -től kölönböző érintője metszi ki AB -ből P-t. /2 látószögű körívét a C -t tartalmazó oldalon. Ennek a CO egyenessel alkotott metszéspontja C’ .Húzzunk párhuzamost C-n keresztül AC’ -vel, metszéspontja AO -val legyen O1, valamint C-n keresztül BC’ -vel, metszéspontja BO -val legyen O2. Az O1 középpontú, AB -t érintő kör C -ből húzott, AC -től kölönböző érintője metszi ki AB -ből P-t.
Igazolás: ABC’ és O1O2C és O1O2C hasonlósága miatt O1O2 párhuzamos AB -vel, e középpontok körüli AB-t érintő körök sugara egyenlő. O1 és O2 rajta vannak az AO ill. BO szögfelezőkön, ezért e körök az AC ill. BC oldalakat is érintik. Legyen ACO1 hasonlósága miatt O1O2 párhuzamos AB -vel, e középpontok körüli AB-t érintő körök sugara egyenlő. O1 és O2 rajta vannak az AO ill. BO szögfelezőkön, ezért e körök az AC ill. BC oldalakat is érintik. Legyen ACO1 = = 1 , BCO2 1 , BCO2 = = 2 . 2 .  1+ 1+ 2= 2= - - /2= /2= /2 Az érintés miatt PCO1 /2 Az érintés miatt PCO1 =ACO1 =ACO1 = = 1 , így PCO2 1 , így PCO2 = = –2. –2. 1- 1- 2= 2= – – /2- /2- 1= 1= /2- /2- 1= 1= 2 , tehát CP az O2 körüli BC -t érintő kört is érinti. 2 , tehát CP az O2 körüli BC -t érintő kört is érinti.
|
 |
|
|
|
| [549] Tibixe | 2010-05-12 22:14:12 |
 Egy pillanatig nem vontam kétségbe a képességeidet.
Arról beszéltem, hogy nem találom fairnek, hogy azzal, hogy az esetlegesen kitűzött könnyű problémák kapcsán leírod, hogy mennyire könnyű, triviális és potya ( tényleg az ), de a nehéz feladatokról nem jegyzed meg, hogy mennyire érdekes/szép/dolgozni kell érte. Majd ebből a nem reprezentatív mintából implicit levonod azt a következtetést, hogy most könnyebb versenyezni az A pontversenyben, bezzeg a hőskor.
Nyilván azért van ez, mert nincs időd végignézegetni, hogy a nem-ötpercesek közül melyik feladat jön ki egy nap, melyik egy hét, és melyik három hét gondolkodás után. Viszont akkor ne vonj le következtetéseket.
Én is elkezdhetném mondani, hogy az N.145. mennyire könnyű volt ( hiszen a területnégyzet az oldalnégyzetekben kvadratikus a Hérón-képlet kifejtett alakja szerint, és éppen akkor pozitív, amikor létezik a háromszög ), de nem teszem, mert fogalmam sincs, hogy a vele együtt kitűzöttek mennyire voltak nehezek vagy könnyűek.
|
| Előzmény: [544] Róbert Gida, 2010-05-12 20:46:06 |
|
| [548] m2mm | 2010-05-12 22:08:40 |
 Ha a 3 közé engem beleszámítasz, én nem akartalak megtámadni, Blanka pedig csak jelezte, hogy már írtad korábbi feladatra is, hogy ilyen potyát még nem láttál A-nak. Tibi pedig szeretne látni tőled egy nehezebb A feladat megoldását.
|
| Előzmény: [544] Róbert Gida, 2010-05-12 20:46:06 |
|
|
|
|
| [544] Róbert Gida | 2010-05-12 20:46:06 |
 Nem tartom fairnek, hogy 3-an jöttök megtámadni egyszerre. Nem tudom, hogy tisztában vagy vele, de már egy ideje leérettségiztem, így nem vagyok aktív Kömal megoldó. De az akkori N jelűek között többször voltam díjazott, régebben ráadásul 4 N feladat volt, nem 3. A múlt havi többi "A" jelűekhez valószínűleg több idő kell, mint 5 perc, amennyi időm volt.
|
| Előzmény: [542] Tibixe, 2010-05-12 18:46:02 |
|
|
| [542] Tibixe | 2010-05-12 18:46:02 |
 Az tény, hogy nekem és szerintem még sokan másoknak nem kellett hozzá 5 perc se, de nem teljesen fair, hogy csak a könnyű feladatokról írsz. Kíváncsi lennék mi a véleményed a rákövetkező feladatról.
( Amire egyébként szívesen látnék megoldást, mert olyan versenyzővel még nem találkoztam akinek sikerült volna. )
|
| Előzmény: [540] Róbert Gida, 2010-05-12 18:14:10 |
|
|
| [540] Róbert Gida | 2010-05-12 18:14:10 |
 (lejárt) A506-os megoldása: legyen az a pontos p hatványosztója pk, ekkor a=m*pk, és a színe legyen m mod p (ez 1,2,...,p-1 lehet, mert m nem osztható p-vel), az a felírása egyértelmű, így a színezés is. Továbbá i*a színe i*a=(i*m)*pk miatt (i*m) mod p, hiszen a pontos osztó pk, ha 0<i<p, de i*m redukált maradékrendszert alkot mod p, ha i befutja az 1,2,...,p-1 számokat, így a színek páronként különbözőek, ami kellett.
Ilyen könnyű A jelűt még nem láttam. 5 perc alatt megoldottam.
|
|
|
|
| [537] R.R King | 2010-04-19 20:01:18 |
 Pontosan erre gondoltam az előző hozzászólásban csak nem volt konkrét ellenpéldám
|
|
|
| [535] R.R King | 2010-04-19 19:58:44 |
 Üdv. Az oszthatóságok rendben vannak, szerintem ott a hiba amikor n-et kifejezed c,d-vel, mert ott már nem mindegy, hogy a +- közül melyik valósul meg ténylegesen.
|
| Előzmény: [534] bily71, 2010-04-19 19:39:38 |
|
|
|
|
|
| [530] D. Tamás | 2010-04-19 16:36:25 |
 A megoldásomban leírtam, hogy legyen (1) 2n+1="anégyzet" és (2) 3n+1="bnégyzet" ahol a és b pozitív egész számok. Namost mi az "anégyzet"+"bnégyzet"+1 értékét akarjuk meghatározni. Ha az (1) egyenlet háromszorosából kivonjuk a (2) egyenlet 2szeresét, akkor az pont előnyünkre válik, hiszen n mint változó kiesik. Innen pedig már szerintem könnyű a feladat, ezt a kis trükköt kellett volna észrevenni, hiszen ekkor 5n+3 felbomlik 2 egész szám szorzatára. (Bár nem írom már le ide, de még azt az esetet kellett vizsgálni, hogy mi van abban az esetben, ha az egyik tényező 1. Ekkor ugye lehet 5n+3 prím is, de itt is ellentmondásra jutunk, tehát nincsen ilyen lehetőség. Bár még nem javították ki a feladatot, de remélem nem hibáztam el semmit sem.
|
|
| [529] rizsesz | 2010-04-19 16:12:16 |
 Mivel osztható egyébként 5n+3, vagy hogy jön ki az, hogy összetett szám? :) Nekem mindenféle drámai fordulat kijött n-re (a 40-gyel oszthatóság biztosan, de mintha fokozódott volna a hangulat...)
|
| Előzmény: [528] D. Tamás, 2010-04-19 15:34:38 |
|
| [528] D. Tamás | 2010-04-19 15:34:38 |
 Nem olvastam végig, de az (iii)-től kezdve lesz a gondolatmenetben a hiba. Talán túlságosan is "túlbonyolítod" ezt a feladatot (Persze ez csak az én véleményem), létezik ennél sokkal egyszerűbb megoldása is, csak egy kicsit trükközni kell.
|
|



 körülírt köre k, beírt körének középpontja O . Az APC és BCP háromszögek beírt k1 , k2 köreinek középpontja O1 ill. O2 . Mivel ezek a körök ABC
körülírt köre k, beírt körének középpontja O . Az APC és BCP háromszögek beírt k1 , k2 köreinek középpontja O1 ill. O2 . Mivel ezek a körök ABC /2 . Nagyítsuk az O középpontból az O1O2C
/2 . Nagyítsuk az O középpontból az O1O2C =
=




 a
a