Fórum: Lejárt határidejű KÖMAL feladatokról

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49]

Szeretnél hozzászólni? Jelentkezz be.

[621] Erben Péter

2010-12-18 10:06:17

Nem maradt ki valami A_n+1 definíciójából?

$A_{n+1} = A_n \prod_{i}^{1\dots f(n)} +1$

a) $A_{n+1} = A_n \prod_{i}^{1\dots f(n)}A_i +1$ ?

b) $A_{n+1} = A_n \prod_{i}^{1\dots f(n)}p_i +1$ ?

c) $A_{n+1} = \prod_{i}^{1\dots f(n)}A_i +1$ ?

Előzmény: [619] Tibixe, 2010-12-17 22:17:28

[620] Erben Péter	2010-12-18 06:55:56
Köszönöm a megoldást és a TeX-elést!
Előzmény: [619] Tibixe, 2010-12-17 22:17:28

[619] Tibixe

2010-12-17 22:17:28

Bemásolom amit kaptam, csak a képleteket írom át texbe. ( az esztétikát úgy általában kispóroltam belőle )

---

A mi sorozatunk azt is tudni fogja, hogy

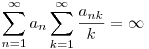
$\sum_{n=1}^{\infty} a_n \sum_{k=1}^{\infty} \frac{a_{nk}}{k}=\infty$

Mivel 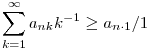$\sum_{k=1}^\infty a_{nk} k^{-1} \ge a_{n \cdot 1}/1$ , ezért ez valóban erősebb, tehát elég ha ilyen sorozatot találunk.

Jelölje először is az i-edik prímet p_i.

Most szükségünk lesz majd egy dologra, méghozzá, hogy a prímek reciprokösszege divergens, ezt nem kell külön igazolnunk, akármelyik számelméletkönyvben megtalálható bizonyítással együtt, mondjuk a Szalay Mihály számelmélet c. könyvben.

Eszerint definiáljuk p_f(n)-t úgy, hogy ez a legkisebb indexű prím, amire 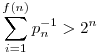$\sum_{i=1}^{f(n)} p_n^{-1} > 2^n$ , ilyen tehát mindenképpen létezik.

Definiáljuk még az A_i sorozatot a következőképpen rekurzíven, legyen A₁=1 és

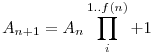
$A_{n+1}=A_n \prod_{i}^{1..f(n)}+1$

Most eljött az ideje, hogy definiáljuk az a_u sorozatunkat:

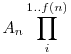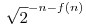Ha A_n $\le$ u<A_n+1, akkor a_u=0, ha u nem többszöröse A_n-nek, vagy u nem osztója $A_n \prod_{i}^{1..f(n)}$ -nek, egyébként pedig $\sqrt{2}^{-n-f(n)}$ .

Bebizonyítom, hogy ez a sorozat jó lesz nekünk, ehhez két dolgot kell látni.

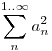$\sum_n^{1..\infty} a_n^2$ véges:

Olyan u egész szám, amire A_n $\le$ u<A_n+1 és u többszöröse A_n-nek és osztója -nek nyilván 2^f(n) db van, hiszen A_n-en kívül még minden prímtényezőt vagy beválasztunk a számba vagy nem, így tehát $\sum_i^{A_n..A_{n+1}-1} a_n^2=2^{f(n)} (\sqrt{2}^{-n-f(n)})^2=2^{-n}$ , amiből:

$\sum_n^{1..\infty} a_n^2=\sum_k^{1..\infty} 2^{-k}=1$

, ami valóban véges.

$\sum_{k=1}^\infty a_{nk} k^{-1}=\infty$ bizonyítása:

Még vezessünk be egy jelölést kényelmi okokból, k $\Delta$ j [sajnos nincs nabla -- tibixe] jelentse azt, hogy létezik olyan n, amelyre A_n $\le$ k,j<A_n+1.

Amit mi igazolunk az, hogy

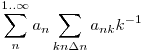
$\sum_n^{1..\infty} a_n \sum_{kn \Delta n} a_{nk} k^{-1}$

, ez nyilván még erősebb, mint amit akartunk.

Felírhatjuk, hogy

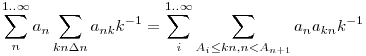
$\sum_n^{1..\infty} a_n \sum_{kn \Delta n} a_{nk} k^{-1}=\sum_i^{1..\infty} \sum_{A_i \le kn, n < A_{n+1}} a_n a_{kn} k^{-1}$

Amit alulról szeretnénk becsülni az 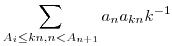$\sum_{A_i \le kn, n < A_{n+1}} a_n a_{kn} k^{-1}$ .

Legyen S_b azoknak az A_i-nál nem kisebb és A_i+1-nél kisebb pozitív egészek halmaza, amelyek többszörösei A_i-nek és osztója 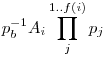$p_b^{-1} A_i \prod_j^{1..f(i)}p_j$ -nek, ahol 1 $\le$ b $\le$ f(i), ezeknek a halmazoknak az elemszáma nyilván 2^f(n)-1.

Ezt a jelölést használva:

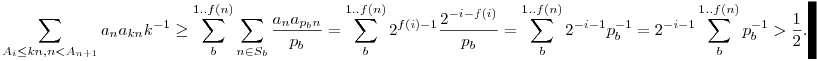
$\sum_{A_i \le kn, n < A_{n+1}} a_n a_{kn} k^{-1} \ge \sum_b^{1..f(n)} \sum_{n \in S_b} \frac{a_n a_{p_b n}}{p_b}=\sum_b^{1..f(n)} 2^{f(i)-1} \frac{2^{-i-f(i)}}{p_b}= \sum_b^{1..f(n)} 2^{-i-1} p_b^{-1}= 2^{-i-1} \sum_b^{1..f(n)} p_b^{-1} > \frac{1}{2}.$

Előzmény: [615] janomo, 2010-12-17 19:51:07

[618] janomo	2010-12-17 20:04:20
na már el is küldtem

[617] Tibixe	2010-12-17 20:01:59
Tényleg? Mert én nem láttam meg rá a triviális bizonyítást, kérlek írd le ide.
Előzmény: [616] Róbert Gida, 2010-12-17 19:53:02

[616] Róbert Gida	2010-12-17 19:53:02
Monotonokra triviális a feladat.
Előzmény: [614] Tibixe, 2010-12-17 17:05:32

[615] janomo

2010-12-17 19:51:07

Hello!

Na az a lényeg hogy van ilyen sorozat, nem tudom föltenni forumra a megoldást, de elküldöm tibinek (tibixe), ő majd felteszi.

Nagy János

Előzmény: [613] Erben Péter, 2010-12-17 13:36:04

[614] Tibixe

2010-12-17 17:05:32

Nemtriviális eredményként nekem annyi jött ki, hogy monoton sorozatokra a kérdéses összeg véges.

Az meg egyszerűen belátható, hogy akkor is véges, ha az a sorozat teljesen multiplikatív.

Előzmény: [613] Erben Péter, 2010-12-17 13:36:04

[613] Erben Péter

2010-12-17 13:36:04

Most, hogy a matematikatanítás helyzetéről szóló eszmecsere külön témába került, szeretnék visszatérni a feladathoz, ami feltüzelte a fórum-társakat.

Bármilyen ötlet és részeredmény is érdekelne az A.520. kapcsán.

Előzmény: [611] m2mm, 2010-12-13 17:10:40

[612] Moderátor	2010-12-15 21:00:44
A matematika oktatás helyzetéről elkezdődött vitát új témába helyeztem át.

[611] m2mm	2010-12-13 17:10:40
Valaki feltenné A. 520. feladat megoldását?

[610] rizsesz	2010-11-25 12:43:11
A K.259 az a két téglalap különbsége, nem, tehát 100, nem?

[609] vogel	2010-11-18 16:08:33
Ilyesmire gondoltam, koszonom Neked.
Előzmény: [607] Lóczi Lajos, 2010-11-18 12:48:23

[608] Róbert Gida	2010-11-18 15:50:53
Ezt én is próbáltam, de Mathematica 5.1 még nem találja meg a megoldást.
Előzmény: [607] Lóczi Lajos, 2010-11-18 12:48:23

[607] Lóczi Lajos

2010-11-18 12:48:23

Ezzel 1 sorban kijön a megoldás (a=90,b=180,c=1740):

Reduce[{a+b+c==2010, 1/a+1/b+1/c==1/58, 0<a<=b<=c},{a,b,c}, Integers]

Előzmény: [598] vogel, 2010-11-14 09:45:06

[606] jonas	2010-11-17 14:51:00
Vigyázz, ha ilyeneket mondassz, hogy „az én időmben”, mindenki bácsizni fog, és szerintem az nem kellemes.
Előzmény: [604] Maga Péter, 2010-11-17 10:02:38

[605] Lóczi Lajos	2010-11-17 12:32:36
Meg tudod írni, hogy pontosan melyik egyenletről és milyen feltételek esetén van szó?
Előzmény: [601] vogel, 2010-11-16 15:00:32

[604] Maga Péter

2010-11-17 10:02:38

,,De a diákok manapság csak a paint-tel festegetnek, meg a word-el vacakolnak.''

Ez már az én időmben is így volt. Alsó tagozaton és gimnáziumban nem tanultam egy betű informatikát sem (nem is volt ilyen órám). Felső tagozaton (akkor jól felszereltnek számító gépterme volt az iskolának) négy év alatt annyit sikerült összehozni, hogy megtanultunk 6-8 DOS-parancsot, meg ezeket Norton Commanderben (sok ész kellett hozzá...). Emellett rengeteget kellett wordben írni. A tanáromnak valamiért az volt az elképzelése, hogy ha a biológia, földrajz stb. könyvek egyes fejezeteit begépelteti velünk, akkor azzal a megfelelő természettudományok mellett az informatikát is elsajátítjuk. Persze mindkét részben tévedett. Programozásról szó sem esett. Nem tudom, a tanárom mennyire tudott programozni. Azt gyanítom, kb. semennyire, de lehet, hogy ez csak az én rosszindulatom; mindazonáltal más iskolákból is hallottam hasonló eseteket.

Valószínűleg a friss tudomány esetében arról van szó, hogy a (főleg általános iskolai, de gyakran még a középiskolai) tanárok felkészültsége is nagyon-nagyon finoman szólva hagy némi kívánnivalót maga után. És egyszerűen azért word meg paint megy az órákon, mert a tanár tudása eddig terjed.

Előzmény: [602] Róbert Gida, 2010-11-16 22:08:46

[603] vogel	2010-11-17 01:41:26
Öhm, csak solve-ra és hasonlókra gondoltam. Én attól is elvárnám a megoldást. Amúgy van, amit az iskolában kevésbé tudnak megtanítani...
Előzmény: [602] Róbert Gida, 2010-11-16 22:08:46

[602] Róbert Gida

2010-11-16 22:08:46

Semmit sem használva, 2 darab for ciklussal még a Mathematica is a gépemen 14 másodperc alatt megtalálja az egyetlen megoldást.

Ennyi programozási alapismeret szerintem elvárható lenne egy mai iskolástól, akárhol tanul. De a diákok manapság csak a paint-tel festegetnek, meg a word-el vacakolnak.

Előzmény: [601] vogel, 2010-11-16 15:00:32

[601] vogel	2010-11-16 15:00:32
Csak hozzászoktam, hogy mindent megold, ezért nagyon meglepett. De ha valaki tudna olyan parancsot, amire kidobja a megoldást, az jó lenne.
Előzmény: [600] Róbert Gida, 2010-11-14 16:28:59

[600] Róbert Gida	2010-11-14 16:28:59
Vacak mathematica, írjál Stephen Wolframnak!
Előzmény: [598] vogel, 2010-11-14 09:45:06

[599] vogel	2010-11-14 10:37:57
Viszont ugyanazokkal a gondolatokkal befejezhető, csak a végén a másodfokú egyenletet meg kell oldani.
Előzmény: [597] Radián, 2010-11-14 08:45:29

[598] vogel	2010-11-14 09:45:06
Egy zárójel felbontást elrontottam, de nekem a Mathematica nem adta ki a megoldást, csak komplexben, egészre pedig üres halmazt. Na mindegy.
Előzmény: [597] Radián, 2010-11-14 08:45:29

[597] Radián

2010-11-14 08:45:29

Tehát ha jól értelmezem, szerinted nincs megfelelő a,b,c szám melyekre mindkét egyenlőség fennállna. Amúgy létezik egyetlen ilyen számhármas a 90,180,1740 . Értem a gondolatmenetedet, de szerintem k=29p+2 alakú , hisz behelyettesítés után (legalábbis én) az alábbi egyenlőséget kaptam:

(29kbc)/58 = 29kb+29kc+bc

0=58k(b+c)+bc(2-k)

Nyilván bc(2-k) osztható 29-cel akkor ha b v c osztható 29-cel nem jön ki ellenkező esetben k=29p+2 alakú.

Előzmény: [596] vogel, 2010-11-13 20:25:50

Már regisztráltál?
Új vendég vagy?