| [636] Róbert Gida | 2011-04-23 21:58:42 |
 Így már érthető. Ha már észrevettem a hipergráfos átfogalmazást, gondoltam megnézem Lovász Kombinatorikai problémák és feladatok c. könyvében, hogy megtalálom-e. 13. fejezet 27. példája pontosan ez, kínairól matematika nyelvére lefordítva (13. fejezet a hipergráfos.) És csak fél métert kellett nyúlnom érte az asztalomon.
janomo, ezt is veheted egy általam elmondott nehéz feladatnak.
|
| Előzmény: [635] Kemény Legény, 2011-04-23 19:10:47 |
|
| [635] Kemény Legény | 2011-04-23 19:10:47 |
 Szerintem félreolvashattál valamit, talán azt, hogy "...amelyre C bármely két elemének és A-nak van közös eleme". Amit te feltételezel, az az, hogy C bármely három elemének kell legyen közös eleme, amit semmi sem garantál.
|
| Előzmény: [634] Róbert Gida, 2011-04-23 18:01:45 |
|
| [634] Róbert Gida | 2011-04-23 18:01:45 |
 Igazad van, a megoldás is fent van már.
Amit nem értek most az a (lejárt) A531, az megoldás, hogy C egy halmazát választom ki A-nak, és akkor persze Nk=k jó lesz, de ez túl könnyű lenne A-nak nem?
Csak a feladatkitűzéshez: ezt miért nem lehetett volna hipergráffal, hiperélekkel megfogalmazni? Kicsit érthetőbb lett volna.
|
| Előzmény: [633] Maga Péter, 2011-04-19 13:31:03 |
|
| [633] Maga Péter | 2011-04-19 13:31:03 |
 Az A.527-528-nál akár még igazad is lehet, bár nem látom be, hogy egy nehéz pontversenyben miért ne lehetnének olykor könnyebb feladatok.
De ugye az A.532-nél nem gondolod komolyan, hogy le*megoldás*ozod másnak a munkáját csupán azért, mert tudsz belőle viccet csinálni? Arról nem is beszélve, hogy n=0 esetén nem lenne a1, viszont a feladat szövegében konkrétan meg van nevezve a1. Ennyit a szellemes *ellenpéldádról*.
|
| Előzmény: [624] Róbert Gida, 2011-04-18 02:07:42 |
|
|
| [631] Róbert Gida | 2011-04-19 00:00:25 |
 Teljesen jó amit a Mathematica ír, ha x-et beírod a két lehetőség közül, akkor az megadja a p értékeket (ez az eredeti 3-adfokú egyenletből is látszik). Mindkét esetben p=1-et kapsz, az eredeti polinom pedig (x+1)(x+2)(x+3).
|
| Előzmény: [630] jonas, 2011-04-18 23:54:11 |
|
|
|
| [628] Róbert Gida | 2011-04-18 23:19:46 |
 Utóbbi 4 hónapban nem tettél fel egy megoldást sem, de mondok jobbat, senki sem, se könnyűt, se nehezet.
A496-ról beszélünk(?), az mikor volt már, annyit nem lapozok vissza.
"Szóval gyere ki egyszer egy nehéz feladat megoldásával" Azzal jöttem, ki. Régen tudod, hogy nevezték az "A" jelű pontversenyt? N-nel, mint "Nehezebb matematika feladatok versenye".
|
| Előzmény: [625] janomo, 2011-04-18 21:02:49 |
|
| [627] Kós Géza | 2011-04-18 23:09:03 |
 Az A.527-et én rontottam el. Olyan változatot akartam, ami ugyan p-ben negyedfokú egyenletre vezet, de ennek van két szép gyöke. Sajnos x=-1 mindig gyök lett... (Mondjuk a feladatnak azt a tulajdonságát nem sikerült elrontani, hogy ezt szántam a februári ,,könnyű'' A-nak. ;-) ) Most már így marad.
Aki szeret számolni, megpróbálkozhat a következő változattal:
A.527.' Határozzuk meg azokat a p valós számokat, amelyekre az x3+p(6x2+11x+6)=0 egyenletnek van két olyan valós gyöke, amelyek különbsége 1.
|
| Előzmény: [625] janomo, 2011-04-18 21:02:49 |
|
|
| [625] janomo | 2011-04-18 21:02:49 |
 Elég érdekes vagy, mért ragadod ki mindig azokat a példákat amik azért vannak betéve hogy legyen valami ziccer, jó nem mondom nem volt idevaló ez a A 527, sőt szerintem is erős tulzás volt, de akkor is szerintem a komalA nagyon is szinvonalas jo verseny és semmit nem veszít a szinvonalából évről évre.
Ami meg A532-t illeti ahelyett hogy fennakadnál trivialitásakon megprobálhatnád a feladat lényegét nézni és belátni a lényegi állatást, persze mivel azt nem tudnád igy ez nyilván jobb taktika, de az hogy az igazi megoldók megoldásait iyen félszarkasztikusan (szarkazmusnak én csak erősebb megmozdulásokat nevezek) le "megoldás"-ozd, hát az egész egyszerüen szánalmas.
Szóval gyere ki egyszer egy nehéz feladat megoldásával, mondjuk A523 A532, A496 satöbbi és akkor kezdheted (mondjuk akkor nem lennél szánalmas, csak önelégült) oltogatni a komalt, addig meg vegyél vissza az arcodból.
Összefoglalva nem igazán komállak most :)
|
| Előzmény: [624] Róbert Gida, 2011-04-18 02:07:42 |
|
| [624] Róbert Gida | 2011-04-18 02:07:42 |
 Márciusi A 532.: n=k=0;a0= 1 ellenpélda, nincs ilyen c. [[A beküldött *megoldásokra* azért kíváncsi lennék.]] 1 ellenpélda, nincs ilyen c. [[A beküldött *megoldásokra* azért kíváncsi lennék.]]
Februári A 527. egy jó 4 évtizede pedig egy sima felvételi feladat is lehetett volna.
Februári A 528. elemien megoldható azért Dirichlet kell hozzá, n=1 triviális megoldás, n>2 nem lehet, mert H-ig (ha H>c, minden c C-re), akkor maximum C-re), akkor maximum 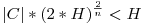 egész áll elő, ha H nagy, ellentmondás. Marad az n=2 eset, ez sem lesz megoldás, elég megmutatni, hogy minden a,b-re tetszőlegesen hosszú intervallumot kihagy az ax2+by2 sorozat. Megmutatom, hogy végtelen sok p prímre, ha ax2+by2 osztható p-vel, akkor osztható p2-tel is. Biz.: tfel osztható p-vel (és legyen p az nem osztója ab-nek), ekkor ax2+by2 egész áll elő, ha H nagy, ellentmondás. Marad az n=2 eset, ez sem lesz megoldás, elég megmutatni, hogy minden a,b-re tetszőlegesen hosszú intervallumot kihagy az ax2+by2 sorozat. Megmutatom, hogy végtelen sok p prímre, ha ax2+by2 osztható p-vel, akkor osztható p2-tel is. Biz.: tfel osztható p-vel (és legyen p az nem osztója ab-nek), ekkor ax2+by2 0mod p, ha y osztható p-vel, akkor x is, de akkor ax2+by2 osztható p2-tel. Ellenkező esetben rendezés után: 0mod p, ha y osztható p-vel, akkor x is, de akkor ax2+by2 osztható p2-tel. Ellenkező esetben rendezés után: 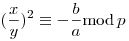 , azaz , azaz 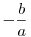 négyzetelem, de akkor (-ab) is, így, ha (-ab) kvadratikus nemmaradék, akkor nem megoldható a kongruencia. Ilyenből pedig végtelen sok van, jobb híján kvadratikus reciprocitási tétellel+Dirichlet-vel kijön. És már itt jönnek a kínaik is: z négyzetelem, de akkor (-ab) is, így, ha (-ab) kvadratikus nemmaradék, akkor nem megoldható a kongruencia. Ilyenből pedig végtelen sok van, jobb híján kvadratikus reciprocitási tétellel+Dirichlet-vel kijön. És már itt jönnek a kínaik is: z p1mod (p1)2;z+1 p1mod (p1)2;z+1 p2mod (p2)2;...;z+u-1 p2mod (p2)2;...;z+u-1 pumod pu2 rendszer megoldható, és éppen ezt szerettük volna, mert akkor egy ilyen z értékre z osztható egy ilyen p-vel, de p2-tel nem, azaz nem áll elő ax2+by2 alakban, és így tovább, z+u-1 sem, azaz u egymásutáni érték. pumod pu2 rendszer megoldható, és éppen ezt szerettük volna, mert akkor egy ilyen z értékre z osztható egy ilyen p-vel, de p2-tel nem, azaz nem áll elő ax2+by2 alakban, és így tovább, z+u-1 sem, azaz u egymásutáni érték.
|
|
|
|
|
|
| [619] Tibixe | 2010-12-17 22:17:28 |
 Bemásolom amit kaptam, csak a képleteket írom át texbe. ( az esztétikát úgy általában kispóroltam belőle )
---
A mi sorozatunk azt is tudni fogja, hogy
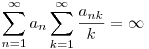
Mivel 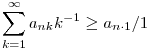 , ezért ez valóban erősebb, tehát elég ha ilyen sorozatot találunk. , ezért ez valóban erősebb, tehát elég ha ilyen sorozatot találunk.
Jelölje először is az i-edik prímet pi.
Most szükségünk lesz majd egy dologra, méghozzá, hogy a prímek reciprokösszege divergens, ezt nem kell külön igazolnunk, akármelyik számelméletkönyvben megtalálható bizonyítással együtt, mondjuk a Szalay Mihály számelmélet c. könyvben.
Eszerint definiáljuk pf(n)-t úgy, hogy ez a legkisebb indexű prím, amire 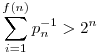 , ilyen tehát mindenképpen létezik. , ilyen tehát mindenképpen létezik.
Definiáljuk még az Ai sorozatot a következőképpen rekurzíven, legyen A1=1 és
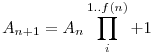
Most eljött az ideje, hogy definiáljuk az au sorozatunkat:
Ha An u<An+1, akkor au=0, ha u nem többszöröse An-nek, vagy u nem osztója u<An+1, akkor au=0, ha u nem többszöröse An-nek, vagy u nem osztója 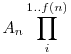 -nek, egyébként pedig -nek, egyébként pedig 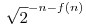 . .
Bebizonyítom, hogy ez a sorozat jó lesz nekünk, ehhez két dolgot kell látni.
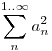 véges: véges:
Olyan u egész szám, amire An u<An+1 és u többszöröse An-nek és osztója -nek nyilván 2f(n) db van, hiszen An-en kívül még minden prímtényezőt vagy beválasztunk a számba vagy nem, így tehát u<An+1 és u többszöröse An-nek és osztója -nek nyilván 2f(n) db van, hiszen An-en kívül még minden prímtényezőt vagy beválasztunk a számba vagy nem, így tehát  , amiből: , amiből:

, ami valóban véges.
 bizonyítása: bizonyítása:
Még vezessünk be egy jelölést kényelmi okokból, k j [sajnos nincs nabla -- tibixe] jelentse azt, hogy létezik olyan n, amelyre An j [sajnos nincs nabla -- tibixe] jelentse azt, hogy létezik olyan n, amelyre An k,j<An+1. k,j<An+1.
Amit mi igazolunk az, hogy
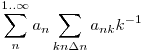
, ez nyilván még erősebb, mint amit akartunk.
Felírhatjuk, hogy
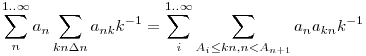
.
Amit alulról szeretnénk becsülni az 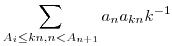 . .
Legyen Sb azoknak az Ai-nál nem kisebb és Ai+1-nél kisebb pozitív egészek halmaza, amelyek többszörösei Ai-nek és osztója 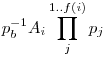 -nek, ahol 1 -nek, ahol 1 b b f(i), ezeknek a halmazoknak az elemszáma nyilván 2f(n)-1. f(i), ezeknek a halmazoknak az elemszáma nyilván 2f(n)-1.
Ezt a jelölést használva:
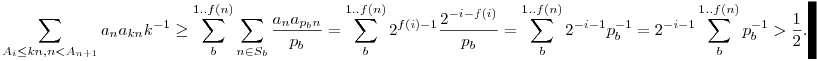
|
| Előzmény: [615] janomo, 2010-12-17 19:51:07 |
|
|
|
|
|
| [614] Tibixe | 2010-12-17 17:05:32 |
 Nemtriviális eredményként nekem annyi jött ki, hogy monoton sorozatokra a kérdéses összeg véges.
Az meg egyszerűen belátható, hogy akkor is véges, ha az a sorozat teljesen multiplikatív.
|
| Előzmény: [613] Erben Péter, 2010-12-17 13:36:04 |
|
| [613] Erben Péter | 2010-12-17 13:36:04 |
 Most, hogy a matematikatanítás helyzetéről szóló eszmecsere külön témába került, szeretnék visszatérni a feladathoz, ami feltüzelte a fórum-társakat.
Bármilyen ötlet és részeredmény is érdekelne az A.520. kapcsán.
|
| Előzmény: [611] m2mm, 2010-12-13 17:10:40 |
|
|








 1 ellenpélda, nincs ilyen c. [[A beküldött *megoldásokra* azért kíváncsi lennék.]]
1 ellenpélda, nincs ilyen c. [[A beküldött *megoldásokra* azért kíváncsi lennék.]]  C-re), akkor maximum
C-re), akkor maximum  0mod p, ha y osztható p-vel, akkor x is, de akkor ax2+by2 osztható p2-tel. Ellenkező esetben rendezés után:
0mod p, ha y osztható p-vel, akkor x is, de akkor ax2+by2 osztható p2-tel. Ellenkező esetben rendezés után: 

 u<An+1, akkor au=0, ha u nem többszöröse An-nek, vagy u nem osztója
u<An+1, akkor au=0, ha u nem többszöröse An-nek, vagy u nem osztója  j [sajnos nincs nabla -- tibixe] jelentse azt, hogy létezik olyan n, amelyre An
j [sajnos nincs nabla -- tibixe] jelentse azt, hogy létezik olyan n, amelyre An