|
| [645] bily71 | 2011-04-29 13:17:39 |
 A feladat szerint az Ai pontok egy kör kerületén helyezkednek el, hát legyen ez a kör az egységsugarú, origó középpontú kör.
A feladat szerint az A1A3 szakasz az A2 pontból  /2n szögben látszik, vagyis az A1,A3 pontok által határolt körív kerületi szöge /2n szögben látszik, vagyis az A1,A3 pontok által határolt körív kerületi szöge  /2n (a pontok egy kör kerületén vannak!), vagyis a körív középponti szöge /2n (a pontok egy kör kerületén vannak!), vagyis a körív középponti szöge  /n. /n.
Az A3A5 szakasz az A4 pontból ugyancsak  /2n szögben látszik, vagyis a szakasz az origóból ugyancsak /2n szögben látszik, vagyis a szakasz az origóból ugyancsak  /n szögben látszik, ez csak úgy lehetséges, ha az A1,A3,A5 pontok egy a körbeírt szabályos 2n-szög csúcsai. Ugyanezt eljátszva az öszes Ai ponttal, ahol i páratlan, kapjuk, hogy az Ai pontok egy szabályos 2n-szög csúcsai. (Persze, az Ai pontok halmaza csak részhalmaza a 2n-szög csúcsai halmazának.) /n szögben látszik, ez csak úgy lehetséges, ha az A1,A3,A5 pontok egy a körbeírt szabályos 2n-szög csúcsai. Ugyanezt eljátszva az öszes Ai ponttal, ahol i páratlan, kapjuk, hogy az Ai pontok egy szabályos 2n-szög csúcsai. (Persze, az Ai pontok halmaza csak részhalmaza a 2n-szög csúcsai halmazának.)
Az is nyílvánvaló, hogy az A1A2n+1 szakasz átmegy az origón. Forgassuk az A1 pontot a (0,1), az A2n+1-et a (0,-1) pontba.
Ugyanígy az Aj pontok is, ahol j páros, egy szabályos 2n szög csúcsai. Az A1A2 szakasz az origóból a feladat szerint tetszőleges  szögben látszik, ahol a feltételek miatt 0 szögben látszik, ahol a feltételek miatt 0    /n, vagyis ezt a 2n-szöget origókörüli, /n, vagyis ezt a 2n-szöget origókörüli,  -szögű forgatással kapjuk az előzőből. -szögű forgatással kapjuk az előzőből.
A feladat szerint az l1 szakasz egyik végpontja az A1 pont (én most azonosítottam a szakasz hosszát magával a szakasszal, ha nem baj), a másikat jelöljük M1-gyel, amely pont egyben az l2 szakasz egyik végpontja, a másikat jelöljük M2-vel, ezt folytatva kapjuk az M1,M2,...,M2n-2 pontokat.
Az A1A2M1, A2M1M2, A3M2M3,...,A2nM2n-2A2n+1 háromszögek hasonlók, hiszen a feladat szerint az A2,A3,...,A2n-1,A2n csúcsokban elhelyezkedő szögek mindegyike  /2n. Ezek egyben váltószögek, hiszen a megfelelő száraik közösek, továbbá az összes háromszög egyik oldala egy egyenesre, az y tengelyre illeszkedik, a így a háromszögek oldalai páronkét párhuzamosak, vagyis hasonlóak. /2n. Ezek egyben váltószögek, hiszen a megfelelő száraik közösek, továbbá az összes háromszög egyik oldala egy egyenesre, az y tengelyre illeszkedik, a így a háromszögek oldalai páronkét párhuzamosak, vagyis hasonlóak.
Mivel a háromszögek hasonlóak, bennük a megfelelő oldalak és a hozzájuk tartozó magasságok aránya állandó, jelöljük ezt c-vel, c 0. 0.
A feladat szerint l12-l22+l32-l42+...-l2n-22+l2n-12=0, vagyis 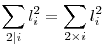 , ahol 1 , ahol 1 i i 2n-1 és ×: "nem osztója". 2n-1 és ×: "nem osztója".
Ha az előző teljesül az li szakaszokra, akkor teljesül a rájuk emelt magasságra is, azaz  (minden li szakasz az előbb részletezett háromszögek közül az egyik alapja), ugyanis mi=lic-t behelyettesítve (minden li szakasz az előbb részletezett háromszögek közül az egyik alapja), ugyanis mi=lic-t behelyettesítve 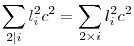 , ebből , ebből 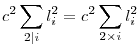 . Mivel c . Mivel c 0, ezért leoszthatunk c2-tel, így visszakapjuk az eredeti állítást, tehát elég az mi-kre belátni. 0, ezért leoszthatunk c2-tel, így visszakapjuk az eredeti állítást, tehát elég az mi-kre belátni.
Vegyük észre, hogy az mi szakasz hossza megegyezik az Ai+1 pontba (ami az mi-hez tartozó háromszög csúcsa) mutató helyvektor x koordinátájának "hosszával", ugyanis az mi-k, mivel magasságok, merőlegesek az alapokra, melyek az y tengelyere illeszkednek, így merőlegesek az y tengelyre, így a vetületük hossza egyenlő az Ai+1 pont vetülete és az origó közti távolsággal, ami definíció szerint épp a pont x koordinátájnak abszolút értéke.
Szerintem még mindig pontatlan, de ha visszamegyünk az axiómákig, akkor sosem érünk a végére.
Folyt. köv.
|
| Előzmény: [641] Maga Péter, 2011-04-29 10:09:22 |
|
|
|
| [642] bily71 | 2011-04-29 10:52:31 |
 "...ez a megoldás hibás, legalábbis erősen hiányos."
Nem hibás, de valóban erősen hiányos, legalábbis az, amit leírtam. Készíts ábrát és azonnal megérted a gondolatmenetem. Ha mégsem, leírom precízebben.
|
| Előzmény: [641] Maga Péter, 2011-04-29 10:09:22 |
|
| [641] Maga Péter | 2011-04-29 10:09:22 |
 Nem oldottam meg a feladatot, nem is nagyon gondolkodtam rajta, úgyhogy a partvonalon túlról szólok (és könnyen lehet, hogy tévedek): ez a megoldás hibás, legalábbis erősen hiányos. Az első két bekezdés már első ránézésre is elképesztő pontatlanságokat tartalmaz. De utána is 'valami bűzlik Dániában', ahogy mondani szokás.
|
| Előzmény: [640] bily71, 2011-04-28 19:15:23 |
|
| [640] bily71 | 2011-04-28 19:15:23 |
 A.530.
Legyen a kör az origó középpontú egységkör, továbbá legyen A1(0,1) és A2n+1(0,-1)!
A kerületi és középponti szögek tételéből következik, hogy az A1, A3,...,A2n+1 pontok egy szabályos 2n-szög csúcsai. Az A2, A4,...,A2n pontok ugyancsak egy szabályos 2n-szög csúcsai, melyet az előbbi 2n-szögből origó körüli  szögű forgatással kapunk (0 szögű forgatással kapunk (0    /n). /n).
Jelöljük az A1A2n+1 és az A2A3, A3A4,...,A2nA2n+1 szakaszok metszéspontjait M1, M2,...,M2n-nel! Ekkor az A1A2M1, A3M1M2,...,A2nM2n-2A2n+1 háromszögek hasonlóak, ugyanis az A1A2M1 , M1A3M2 , M1A3M2 ,...,M2n-2,A2nA2n+1 ,...,M2n-2,A2nA2n+1 szögek váltószögek és a háromszögek alapjai egy egynesre (az y tengelyre) esnek, így az oldalaik páronként párhuzamosak. szögek váltószögek és a háromszögek alapjai egy egynesre (az y tengelyre) esnek, így az oldalaik páronként párhuzamosak.
Mivel a hárömszögek hasonlóak, az alap és a ráemelt magasság aránya mindegyikben megegyezik, vagyis mi/ i=c i=c  mi= mi= ic ic  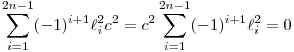 , c , c 0 0   . Tehát elég azt megmutatni, hogy . Tehát elég azt megmutatni, hogy 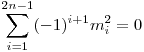 teljesül. teljesül.
Vegyük észre, hogy a magasság hossza a háromszög alapjával szemközti csúcsába mutató helyvektor x koordinátájának abszolút értékével egyezik meg.
Legyenek egy szabályos n-szög csúcsainak koordinátái x1,y1, x2,y2, ...,xn,yn, ekkor 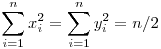 . (A bizonyítást, ha szükséges, leírom.) . (A bizonyítást, ha szükséges, leírom.)
Ha az A3, A5,...,A2n+1 pontokat tükrözzük az origóra, akkor egy szabályos 2n-szöget kapunk. Mivel az Ai és az Ai' pontok x koordinátáinak abszolút értéke megyegyezik, ezért  . Ugyanígy eljárva az A2, A4,...,A2n pontokkal kapjuk, hogy . Ugyanígy eljárva az A2, A4,...,A2n pontokkal kapjuk, hogy 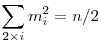 , (×: nem osztható) ebből , (×: nem osztható) ebből   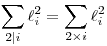   , vagyis az állítás igaz. , vagyis az állítás igaz.
|
|
|
| [638] jonas | 2011-04-24 13:18:05 |
 Ez gyors volt. Nekem majdnem egy évbe telt, amíg megtaláltam a Lovászban, pedig hamarabb kellett volna. Most már egyébként három lényegesen különböző megoldást is tudok a feladatra. Ha gondolod, szorgalmi feladatként találd meg mind a hármat.
Azzal vitatkoznék, hogy hipergráfokkal egyszerűbb a megfogalmazás. Szerintem nem, de más is mondta már, hogy igen.
|
| Előzmény: [636] Róbert Gida, 2011-04-23 21:58:42 |
|
|
| [636] Róbert Gida | 2011-04-23 21:58:42 |
 Így már érthető. Ha már észrevettem a hipergráfos átfogalmazást, gondoltam megnézem Lovász Kombinatorikai problémák és feladatok c. könyvében, hogy megtalálom-e. 13. fejezet 27. példája pontosan ez, kínairól matematika nyelvére lefordítva (13. fejezet a hipergráfos.) És csak fél métert kellett nyúlnom érte az asztalomon.
janomo, ezt is veheted egy általam elmondott nehéz feladatnak.
|
| Előzmény: [635] Kemény Legény, 2011-04-23 19:10:47 |
|
| [635] Kemény Legény | 2011-04-23 19:10:47 |
 Szerintem félreolvashattál valamit, talán azt, hogy "...amelyre C bármely két elemének és A-nak van közös eleme". Amit te feltételezel, az az, hogy C bármely három elemének kell legyen közös eleme, amit semmi sem garantál.
|
| Előzmény: [634] Róbert Gida, 2011-04-23 18:01:45 |
|
| [634] Róbert Gida | 2011-04-23 18:01:45 |
 Igazad van, a megoldás is fent van már.
Amit nem értek most az a (lejárt) A531, az megoldás, hogy C egy halmazát választom ki A-nak, és akkor persze Nk=k jó lesz, de ez túl könnyű lenne A-nak nem?
Csak a feladatkitűzéshez: ezt miért nem lehetett volna hipergráffal, hiperélekkel megfogalmazni? Kicsit érthetőbb lett volna.
|
| Előzmény: [633] Maga Péter, 2011-04-19 13:31:03 |
|
| [633] Maga Péter | 2011-04-19 13:31:03 |
 Az A.527-528-nál akár még igazad is lehet, bár nem látom be, hogy egy nehéz pontversenyben miért ne lehetnének olykor könnyebb feladatok.
De ugye az A.532-nél nem gondolod komolyan, hogy le*megoldás*ozod másnak a munkáját csupán azért, mert tudsz belőle viccet csinálni? Arról nem is beszélve, hogy n=0 esetén nem lenne a1, viszont a feladat szövegében konkrétan meg van nevezve a1. Ennyit a szellemes *ellenpéldádról*.
|
| Előzmény: [624] Róbert Gida, 2011-04-18 02:07:42 |
|
|
| [631] Róbert Gida | 2011-04-19 00:00:25 |
 Teljesen jó amit a Mathematica ír, ha x-et beírod a két lehetőség közül, akkor az megadja a p értékeket (ez az eredeti 3-adfokú egyenletből is látszik). Mindkét esetben p=1-et kapsz, az eredeti polinom pedig (x+1)(x+2)(x+3).
|
| Előzmény: [630] jonas, 2011-04-18 23:54:11 |
|
|
|
| [628] Róbert Gida | 2011-04-18 23:19:46 |
 Utóbbi 4 hónapban nem tettél fel egy megoldást sem, de mondok jobbat, senki sem, se könnyűt, se nehezet.
A496-ról beszélünk(?), az mikor volt már, annyit nem lapozok vissza.
"Szóval gyere ki egyszer egy nehéz feladat megoldásával" Azzal jöttem, ki. Régen tudod, hogy nevezték az "A" jelű pontversenyt? N-nel, mint "Nehezebb matematika feladatok versenye".
|
| Előzmény: [625] janomo, 2011-04-18 21:02:49 |
|
| [627] Kós Géza | 2011-04-18 23:09:03 |
 Az A.527-et én rontottam el. Olyan változatot akartam, ami ugyan p-ben negyedfokú egyenletre vezet, de ennek van két szép gyöke. Sajnos x=-1 mindig gyök lett... (Mondjuk a feladatnak azt a tulajdonságát nem sikerült elrontani, hogy ezt szántam a februári ,,könnyű'' A-nak. ;-) ) Most már így marad.
Aki szeret számolni, megpróbálkozhat a következő változattal:
A.527.' Határozzuk meg azokat a p valós számokat, amelyekre az x3+p(6x2+11x+6)=0 egyenletnek van két olyan valós gyöke, amelyek különbsége 1.
|
| Előzmény: [625] janomo, 2011-04-18 21:02:49 |
|
|
| [625] janomo | 2011-04-18 21:02:49 |
 Elég érdekes vagy, mért ragadod ki mindig azokat a példákat amik azért vannak betéve hogy legyen valami ziccer, jó nem mondom nem volt idevaló ez a A 527, sőt szerintem is erős tulzás volt, de akkor is szerintem a komalA nagyon is szinvonalas jo verseny és semmit nem veszít a szinvonalából évről évre.
Ami meg A532-t illeti ahelyett hogy fennakadnál trivialitásakon megprobálhatnád a feladat lényegét nézni és belátni a lényegi állatást, persze mivel azt nem tudnád igy ez nyilván jobb taktika, de az hogy az igazi megoldók megoldásait iyen félszarkasztikusan (szarkazmusnak én csak erősebb megmozdulásokat nevezek) le "megoldás"-ozd, hát az egész egyszerüen szánalmas.
Szóval gyere ki egyszer egy nehéz feladat megoldásával, mondjuk A523 A532, A496 satöbbi és akkor kezdheted (mondjuk akkor nem lennél szánalmas, csak önelégült) oltogatni a komalt, addig meg vegyél vissza az arcodból.
Összefoglalva nem igazán komállak most :)
|
| Előzmény: [624] Róbert Gida, 2011-04-18 02:07:42 |
|
| [624] Róbert Gida | 2011-04-18 02:07:42 |
 Márciusi A 532.: n=k=0;a0= 1 ellenpélda, nincs ilyen c. [[A beküldött *megoldásokra* azért kíváncsi lennék.]] 1 ellenpélda, nincs ilyen c. [[A beküldött *megoldásokra* azért kíváncsi lennék.]]
Februári A 527. egy jó 4 évtizede pedig egy sima felvételi feladat is lehetett volna.
Februári A 528. elemien megoldható azért Dirichlet kell hozzá, n=1 triviális megoldás, n>2 nem lehet, mert H-ig (ha H>c, minden c C-re), akkor maximum C-re), akkor maximum 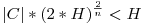 egész áll elő, ha H nagy, ellentmondás. Marad az n=2 eset, ez sem lesz megoldás, elég megmutatni, hogy minden a,b-re tetszőlegesen hosszú intervallumot kihagy az ax2+by2 sorozat. Megmutatom, hogy végtelen sok p prímre, ha ax2+by2 osztható p-vel, akkor osztható p2-tel is. Biz.: tfel osztható p-vel (és legyen p az nem osztója ab-nek), ekkor ax2+by2 egész áll elő, ha H nagy, ellentmondás. Marad az n=2 eset, ez sem lesz megoldás, elég megmutatni, hogy minden a,b-re tetszőlegesen hosszú intervallumot kihagy az ax2+by2 sorozat. Megmutatom, hogy végtelen sok p prímre, ha ax2+by2 osztható p-vel, akkor osztható p2-tel is. Biz.: tfel osztható p-vel (és legyen p az nem osztója ab-nek), ekkor ax2+by2 0mod p, ha y osztható p-vel, akkor x is, de akkor ax2+by2 osztható p2-tel. Ellenkező esetben rendezés után: 0mod p, ha y osztható p-vel, akkor x is, de akkor ax2+by2 osztható p2-tel. Ellenkező esetben rendezés után: 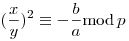 , azaz , azaz 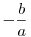 négyzetelem, de akkor (-ab) is, így, ha (-ab) kvadratikus nemmaradék, akkor nem megoldható a kongruencia. Ilyenből pedig végtelen sok van, jobb híján kvadratikus reciprocitási tétellel+Dirichlet-vel kijön. És már itt jönnek a kínaik is: z négyzetelem, de akkor (-ab) is, így, ha (-ab) kvadratikus nemmaradék, akkor nem megoldható a kongruencia. Ilyenből pedig végtelen sok van, jobb híján kvadratikus reciprocitási tétellel+Dirichlet-vel kijön. És már itt jönnek a kínaik is: z p1mod (p1)2;z+1 p1mod (p1)2;z+1 p2mod (p2)2;...;z+u-1 p2mod (p2)2;...;z+u-1 pumod pu2 rendszer megoldható, és éppen ezt szerettük volna, mert akkor egy ilyen z értékre z osztható egy ilyen p-vel, de p2-tel nem, azaz nem áll elő ax2+by2 alakban, és így tovább, z+u-1 sem, azaz u egymásutáni érték. pumod pu2 rendszer megoldható, és éppen ezt szerettük volna, mert akkor egy ilyen z értékre z osztható egy ilyen p-vel, de p2-tel nem, azaz nem áll elő ax2+by2 alakban, és így tovább, z+u-1 sem, azaz u egymásutáni érték.
|
|
|
|



 /2n szögben látszik, vagyis az A1,A3 pontok által határolt körív kerületi szöge
/2n szögben látszik, vagyis az A1,A3 pontok által határolt körív kerületi szöge  szögben látszik, ahol a feltételek miatt 0
szögben látszik, ahol a feltételek miatt 0
 0.
0. 
 , M1A3M2
, M1A3M2 i=c
i=c  mi=
mi=




 1 ellenpélda, nincs ilyen c. [[A beküldött *megoldásokra* azért kíváncsi lennék.]]
1 ellenpélda, nincs ilyen c. [[A beküldött *megoldásokra* azért kíváncsi lennék.]]  C-re), akkor maximum
C-re), akkor maximum  0mod p, ha y osztható p-vel, akkor x is, de akkor ax2+by2 osztható p2-tel. Ellenkező esetben rendezés után:
0mod p, ha y osztható p-vel, akkor x is, de akkor ax2+by2 osztható p2-tel. Ellenkező esetben rendezés után: 