| [671] Szabó Attila | 2011-08-15 22:18:12 |
 Nem tudja valaki, hogy miért nem kapott senki pontot a májusi mérési feladatra és miért nem javították ki a beküldött dolgozatokat?
|
|
|
|
| [668] Róbert Gida | 2011-08-12 18:01:19 |
 Voltak már hasonló példák, leginkább az S(2n) nem korlátos ősrégi N jelű feladatra gondolok.
B4360: Belátom először, hogy k=2 jó. Részben indukcióval csinálom. Állításom: 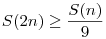 . Ez n<10-re teljesül. Ha n . Ez n<10-re teljesül. Ha n 10 és n-nek van 5-nél kisebb számjegye, akkor ott elvágjuk n-et és indukcióval teljesül az állítás n-re is. Így feltehető, hogy n minden jegye legalább 5, akkor minden helyiértéken van átvitel a szorzásnál, így a következő jegy a szorzatban nem lehet nulla, hiszen (2*d+1)mod 10 a jegy, ami páratlan, így nem nulla. Azaz L jegyű n esetén S(n) 10 és n-nek van 5-nél kisebb számjegye, akkor ott elvágjuk n-et és indukcióval teljesül az állítás n-re is. Így feltehető, hogy n minden jegye legalább 5, akkor minden helyiértéken van átvitel a szorzásnál, így a következő jegy a szorzatban nem lehet nulla, hiszen (2*d+1)mod 10 a jegy, ami páratlan, így nem nulla. Azaz L jegyű n esetén S(n) 9L (ez trivi), míg S(2n) 9L (ez trivi), míg S(2n) L, hiszen a rákövetkező jegy mindig legalább 1. Kettőből: L, hiszen a rákövetkező jegy mindig legalább 1. Kettőből: 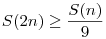 , ami kellett. Teljesen hasonló a biz. k=5-re is. Indukcióval ebből: , ami kellett. Teljesen hasonló a biz. k=5-re is. Indukcióval ebből: 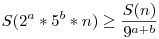 , így, ha k=2a*5b, akkor az megoldás lesz. , így, ha k=2a*5b, akkor az megoldás lesz.
Más megoldás nincs: legyen k az L jegyű, így k<10L. Legyen N L tetszőleges, és w az az egyértelmű k-val osztható egész, amelyre w=10N+r, ahol 0 L tetszőleges, és w az az egyértelmű k-val osztható egész, amelyre w=10N+r, ahol 0 r<k teljesül. Ekkor r=0 nem lehet, különben k|10N, de k akkor 2a*5b alakú szám lenne, ellentmondás. w osztható k-val, így legyen r<k teljesül. Ekkor r=0 nem lehet, különben k|10N, de k akkor 2a*5b alakú szám lenne, ellentmondás. w osztható k-val, így legyen 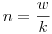 . Indirekt feltevés miatt S(kn) . Indirekt feltevés miatt S(kn) ckS(n), innen: ckS(n), innen: 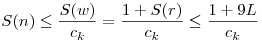 , azaz S(n) korlátos. (L és ck is konstans). És ez nem lehet. , azaz S(n) korlátos. (L és ck is konstans). És ez nem lehet.
Legyen n 10-es számrendszeres ábrázolása:

, ahol di>0 és az a0<a1<...<as-1. Ekkor a0 L, minden i-re, ai-ai-1 L, minden i-re, ai-ai-1 L, as-1 L, as-1 N-L, ezekből már kövekezni fog az ellentmondás, mert ekkor indukcióval: ai N-L, ezekből már kövekezni fog az ellentmondás, mert ekkor indukcióval: ai (i+1)L, de as-1 (i+1)L, de as-1 N-L, így N-L, így 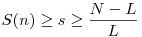 , azaz S(n) nem korlátos, ellentmondás. , azaz S(n) nem korlátos, ellentmondás.
Ha a0>L, akkor n osztható 10L-el, de akkor w=kn is, ellentmondás, mert N L, így w az 10L-el osztva r maradékot ad, de r nem nulla. w>10N és k<10L, így L, így w az 10L-el osztva r maradékot ad, de r nem nulla. w>10N és k<10L, így  , ezért as-1 , ezért as-1 N-L. Végül minden i-re ai N-L. Végül minden i-re ai ai-1+L, indirekte legyen: at>at-1+L esetén tekintsük az ai-1+L, indirekte legyen: at>at-1+L esetén tekintsük az  , tekintsük ezt modulo 10at, ekkor , tekintsük ezt modulo 10at, ekkor 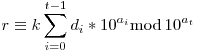 , ez modulo nélkül is teljesül egyenlőséggel, mert k<10L és at-1+L<at. Azaz , ez modulo nélkül is teljesül egyenlőséggel, mert k<10L és at-1+L<at. Azaz 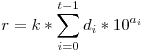 , jobb oldal osztható k-val, de a bal oldal nem, ellentmondás. , jobb oldal osztható k-val, de a bal oldal nem, ellentmondás.
|
| Előzmény: [663] Róbert Gida, 2011-08-12 01:09:50 |
|
|
| [666] Lóczi Lajos | 2011-08-12 14:29:44 |
 Csak óvatosan! A 2.) lépésbeli 2. állításod általában nem igaz! Egy függvény grafikonja és inverze grafikonjának metszéspontja "bárhol" lehet!
Ezzel kapcsolatban lásd a megfelelő KöMaL-cikket, amely pl. elérhető itt:
www.berzsenyi.hu/erben/rlv/2010/abraham_gabor.ppt
|
| Előzmény: [665] sakkmath, 2011-08-12 14:09:05 |
|
| [665] sakkmath | 2011-08-12 14:09:05 |
 Vázlat B.4358.-hoz:
1) Belátjuk, hogy 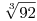 és -11 nem gyökei az egyenletnek, s ezért a gyökökhöz ezt az egyenletet vizsgáljuk: és -11 nem gyökei az egyenletnek, s ezért a gyökökhöz ezt az egyenletet vizsgáljuk:
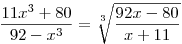
2) Belátjuk, hogy a bal oldalon álló függvény a jobb oldalon álló inverze. A derékszögű koordinátarendszerben e két fv. grafikonja az y=x egyenesen metszi egymást.
3) A jobb (vagy a bal) oldalon álló kifejezést x - szel egyenlővé tesszük és a rendezések után ezt kapjuk:
x4+11x3-92x+80=0
4) Feltesszük, hogy van egész gyök. A szóba jövő egész gyökök a konstans tag osztói, ezért behelyettesítésekkel hamar kijön, hogy a gyökök: -10,-4,1 és 2.
|
| Előzmény: [661] Blinki Bill, 2011-08-11 20:39:23 |
|
|
|
| [662] Róbert Gida | 2011-08-12 00:13:30 |
 B4358 Feladat nem írja (miért is írná), de csak a valós megoldásokat keressük (köbgyökvonás a komplexeknél már nem is egyértelmű). Az egyik tagot átviszem a másik oldalra, köbre emelem, hogy eltűnjön a köbgyök, rendezem, kapok egy 10-edfokú egyenletet:
1423*x10+14561*x9+3648*x7+341520*x6+2547264*x4+291840*x3-71127296*x+67927040=0 (Mathematica szerint) ennek -10,-4,1,2 gyöke, és a feladatnak is (ellenőrzés). A maradó polinom hatodfokú: g(x)=1423*x6-1092*x5+12012*x4+2432*x3+100464*x2+87360*x+849088. Ennek már nincs valós gyöke: |x|<1-re a konstans tag miatt pozitiv g(x), míg |x|>1-re: 1423*x6 1092*x5, 12012*x4 1092*x5, 12012*x4 -2432*x3, 100464*x2 -2432*x3, 100464*x2 -87360*x, egyenlőtlenségeket használva: g(x)>0 itt is. -87360*x, egyenlőtlenségeket használva: g(x)>0 itt is.
|
| Előzmény: [661] Blinki Bill, 2011-08-11 20:39:23 |
|
| [661] Blinki Bill | 2011-08-11 20:39:23 |
 Sziasztok!
Feltenné vki a B.4358. és B.4360. feladatok megoldását?
Köszönöm: Blanka
|
|
| [660] Lóczi Lajos | 2011-08-10 16:28:48 |
 Mathematica 7-ben ha a feladatkitűzésnek megfelelően írjuk be a képleteket, akkor egy bonyolult logikai kombinációt ad ki eredményül, amelyről kideríthetjük, hogy azonosan igaz. Ám ha a konklúzióbeli egyenlőtlenség tagadását írjuk be, indirekt bizonyítás-szerűen, akkor a Reduce pár másodperc alatt kiadja, hogy "azonosan hamis".
|
| Előzmény: [659] Róbert Gida, 2011-08-09 00:27:07 |
|
| [659] Róbert Gida | 2011-08-09 00:27:07 |
 Nézzük meg tudja-e oldani a Mathematica az A jelű feladatot:
a = (b*c*d - b - c - d)/(1 - b*c - b*d - c*d);
Timing[FullSimplify[(a + b)*(c + d) + (a + d)*(b + c) >= 4*Sqrt[(1 + a*c)*(1 + b*d)], a > 0 && b > 0 && c > 0 && d > 0]]
{21.965 Second, True}
Húha, megdolgozott a Mathematica a válaszért. Kicsit segítettem is neki, ha az "a"-t nem fejezem ki, akkor nem bizonyítja be, visszaadja az eredetit. Az persze kérdéses, hogy minden esetben szabályos-e ez, azaz amivel leosztok az nem nulla, esetleg b-vel, c-vel, d-vel eljátszhatom ezt, ha "a"-val nem.
|
| Előzmény: [657] Tibixe, 2011-07-01 14:05:57 |
|
| [658] Janosov Milán | 2011-08-03 00:57:06 |
 Valaki tudja, az utolsó mérési feladat fura statisztikájának mi a magyarázata?
|
|
| [657] Tibixe | 2011-07-01 14:05:57 |
 Elég rögtön használni a számtani-mértani egyenlőtlenséget, homogenizálni és átrendezni.
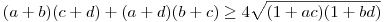
A számtani és mértani közép közti egyenlőtlenség miatt  . Ezért erősebb állítás, hogy . Ezért erősebb állítás, hogy
(a+b)(c+d)+(a+d)(b+c) 4+2ac+2bd 4+2ac+2bd
Kifejtve és kivonva:
ad+bc+ab+cd 4 4
A feltétellel szerint a+b+c+d=abc+abd+acd+bcd és itt mindkét oldal pozitív, tehát utóbbi két oldalával ekvivalens átalakításként szorozhatjuk az állítást:
(a+b+c+d)(ad+bc+ab+cd) 4(abc+abd+acd+bcd) 4(abc+abd+acd+bcd)
A zárójeleket felbontva és nullára rendezve:
a2b+a2d+ab2-2abc-2abd-2acd+ad2+b2c+bc2-2bcd+c2d+cd2 0 0
Ezt átírva:
(a+c)(b-d)2+(b+d)(a-c)2 0 0
Ez nyilván teljesül, mert nemnegatív teljes négyzetek nemnegatív együtthatós polinomja is nemnegatív.
|
| Előzmény: [655] sakkmath, 2011-07-01 08:44:32 |
|
|
| [655] sakkmath | 2011-07-01 08:44:32 |
 A KöMaL 2011/5-ös, májusi
számában megjelent
A.536. feladat egyik megoldása:
|
 |
|
| [654] Ali | 2011-06-03 07:53:07 |
 "Csak az a=b=1 esetet hagyod akkor ki."
Vszínűleg elkerülte a figyelmedet az utolsó mondat:
Ha pedig a=b 1, akkor a2c+1|2a2 -ből triviálisan következik, hogy c=1 és a=1. 1, akkor a2c+1|2a2 -ből triviálisan következik, hogy c=1 és a=1.
|
| Előzmény: [653] Róbert Gida, 2011-06-01 16:58:08 |
|
| [653] Róbert Gida | 2011-06-01 16:58:08 |
 "Legyenek először a és b relatív prímek (a,b)=1 és a>b (a>b feltehető, mivel a feladat a-ban és b-ben szimmetrikus)"
Csak az a=b=1 esetet hagyod akkor ki.
Szép megoldás. Amikor megláttam a feladatot nekem egyből a Válogatott feladatok és tételek az elemi matematika köréből (Aritmetika és algebra) 118. csillagos feladata ugrott be, nem tévedtem, a megoldás (és az egyenlet) hasonló: x2+y2+z2=kxyz. Ennek a feladatnak egy általánosítását már egyszer elsütötték A feladatként. Érdemes megvenni a könyvet.
|
| Előzmény: [652] Ali, 2011-06-01 16:00:37 |
|
| [652] Ali | 2011-06-01 16:00:37 |
 Megoldás A.533. -ra: Határozzuk meg mindazokat a pozitív egészekből álló (a,b,c) számhármasokat, amelyekre a2+b2 osztható (abc+1)-gyel.
Legyenek először a és b relatív prímek (a,b)=1 és a>b (a>b feltehető, mivel a feladat a-ban és b-ben szimmetrikus). Legyen továbbá k 1 olyan egész,melyre 1 olyan egész,melyre
Ha b>1 (b=1 eset később tisztázva bn=1-nél), akkor legyenek a1=b és b1=kbc-a. Ekkor fennál, hogy
Biz.: írjuk vissza a1 és b1 helyébe b-t és kbc-a-t: b2+(kbc-a)2=k(b(kbc-a)c+1). Rendezés után (1)-et kapjuk.
Fennáll továbbá, hogy 0<b1<b.
Biz.: k(a1b1c+1)=a12+b12 1 -ből következik, hogy a1b1c 1 -ből következik, hogy a1b1c 1/k-1>-1. Mivel a1 és c pozítív egészek és b1 egész, azért b1 1/k-1>-1. Mivel a1 és c pozítív egészek és b1 egész, azért b1 0. Felhasználva továbbá azt, hogy (a,b)=1 következik, hogy b1=(kbc-a)>0. Másrészt bb1<ab1=a(kbc-a)=b2-k<b2, tehát b1<b és nyilván b=a1<a. (a,b)=1-ből következik, hogy (b,kbc-a)=1, tehát (a1,b1)=1 is fennáll. 0. Felhasználva továbbá azt, hogy (a,b)=1 következik, hogy b1=(kbc-a)>0. Másrészt bb1<ab1=a(kbc-a)=b2-k<b2, tehát b1<b és nyilván b=a1<a. (a,b)=1-ből következik, hogy (b,kbc-a)=1, tehát (a1,b1)=1 is fennáll.
Azt kaptuk, hogy (a1,b1,c,k) -ra szintén teljesül (1).
Folytassuk a rekurziót egészen addig, míg b értéke 1 lesz. A rekurziós képlet:
| ai=bi-1,bi=kbi-1c-ai-1 | (3) |
A fenti gondolatmenetet megismételve kapjuk, hogy bi<bi-1=ai<ai-1 és (ai,bi)=1.
Legyen tehát an=bn-1,bn=kbn-1c-an-1=1. Ekkor an2+1=k(anc+1) és ezért anc+1|an2+1. Áll.: ez csak akkor lehetséges, ha an=c és k=1.
Biz.:Tegyük fel, hogy létezik c<an és l>1 úgy, hogy l(anc+1)=an2+1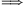 an(an-lc)=l-1>0. Ezért egyrészt an|l-1 és így an<l, másrészt an-lc>0, ebből pegig an>lc an(an-lc)=l-1>0. Ezért egyrészt an|l-1 és így an<l, másrészt an-lc>0, ebből pegig an>lc l l
következik,ami ellentmondás. Tehát an=c és k=1, továbbá an=bn-1>1 miatt c>1.
A (3) lineáris másodrendű rekurziót visszafelé megoldva a bn=1 és az an=c értékekből kiindulva c>2 esetén 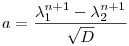 és és  , ahol , ahol 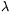 1,2 az x2-cx+1=0 egyenlet gyökei ( 1,2 az x2-cx+1=0 egyenlet gyökei (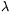 1> 1>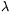 2), D az egyenlet diszkriminánsa és n 2), D az egyenlet diszkriminánsa és n 1. 1.
c=2 esetén a rekurzió az a=n+1 és b=n megoldást adja, ahol szintén n 1. 1.
Ezek pedig mind megoldások is. Ennek bizonyítása egyszerűen visszahelyettesítéssel történhet felhasználva, hogy 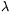 1+ 1+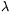 2=c, 2=c, 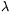 1. 1.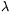 2=1 és D=c2-4, k=1. 2=1 és D=c2-4, k=1.
Nevezzük a továbbiakban az (a,b,c) hármast relatív prím megoldásnak, ha (a,b)=1. Legyen most (a,b,c) egy relatív prím megoldás, ahol c=d2c1, d>1, c1 1. Ilyen megoldás láttuk létezik. Ekkor (ad,bd,c1) egy nem relatív prím megoldás lesz, mivel (ad)(bd)c1+1=ab(d2c1)+1|a2+b2|(da)2+(db)2 1. Ilyen megoldás láttuk létezik. Ekkor (ad,bd,c1) egy nem relatív prím megoldás lesz, mivel (ad)(bd)c1+1=ab(d2c1)+1|a2+b2|(da)2+(db)2
Fordítva legyen (a,b,c) egy nem relatív prím megoldás (előbb láttuk ilyen létezik), melyben (a,b)=d>1, a=a1d, b=b1d, (a1,b1)=1. Ekkor mivel a1b1d2c+1|d2(a12+b12) és (a1b1d2c+1,d)=1, azért a1b1d2c+1|(a12+b12), tehát (a1,b1,d2c) egy relatív prím megoldás. Így minden nem relatív prím megoldás egyértelműen előáll egy relatív prím (a,b,c) megoldásból (ad,bd,c1) formában, ahol c=d2c1, d>1 és c1 1. 1.
Végül marad a c=1 eset. Láttuk, hogy relatív prím megoldás nem létezik c=1 esetén (ahhoz c>1 kellett). A nem relatív prím megoldások pedig azok az (ad,bd,1) alakú megoldások, melyekben (a,b,d2) egy relatív prím megoldás, ahol d>1.
Ha pedig a=b 1, akkor a2c+1|2a2 -ből triviálisan következik, hogy c=1 és a=1. 1, akkor a2c+1|2a2 -ből triviálisan következik, hogy c=1 és a=1.
|
|
| [651] Róbert Gida | 2011-05-13 21:44:51 |
 Lejárt C1076. közölt megoldása érdekes.
Az ember azt hinné, hogy egy C feladatot azért nem lehet elszúrni, de mégis: "A gyökökre vonatkozó feltétel szerint a(a+1)-1=(a+1)2-a2" és itt van a hiba, a feladat a két gyök különbségéről beszélt, és még azt sem mondta, hogy a nagyobbikból a kisebbiket vonjuk ki. De, ha ezt feltesszük akkor is rossz, lásd a=-2, amikor (a+1)2-a2<0 teljesül.
Ki lehet számolni, nem jön be új megoldás, igazából ugyanezeket kapjuk meg még egyszer, de a közölt megoldás elvi hibás marad.
|
|
| [650] Róbert Gida | 2011-05-03 00:25:12 |
 Másik biz.: 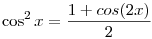 . De . De  , használjuk, hogy a csúcsok n, illetve n/2 csúcsú (minden csúcs 2-szer) szabályos sokszög csúcsaiba mennek át, attól függően, hogy n ptlan vagy ps, továbbá azt, hogy a szab. sokszög súlypontja az origó. Ebből már következik az állítás (n darab 1/2 lesz az összeg). Sinusra hasonló süthető el, vagy használjuk, hogy cos2x+sin2x=1 , használjuk, hogy a csúcsok n, illetve n/2 csúcsú (minden csúcs 2-szer) szabályos sokszög csúcsaiba mennek át, attól függően, hogy n ptlan vagy ps, továbbá azt, hogy a szab. sokszög súlypontja az origó. Ebből már következik az állítás (n darab 1/2 lesz az összeg). Sinusra hasonló süthető el, vagy használjuk, hogy cos2x+sin2x=1
|
| Előzmény: [648] bily71, 2011-05-02 21:43:27 |
|
|
| [648] bily71 | 2011-05-02 21:43:27 |
 Állítás:
Legyenek az origó középpontú, egységsugarú kör kerületére illeszkedő P1(x1,y1),P2(x2,y2),...,Pn(xn,yn) pontok egy szabályos n-szög csúcsai, ekkor 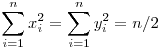 . .
Bizonyítás:
Legyen n=4m, húzzuk be az origón átmenő átlókat, ekkor van m darab egymásra merőleges átlópárunk (n,m N). N).
Tekintsük az AmA3m, A2mA4m átlópárt. Ha az Am pontba mutató vektor az x tengellyel  szöget zár be, akkor a koordináták így alakulnak Pm(cos szöget zár be, akkor a koordináták így alakulnak Pm(cos ,sin ,sin ),P2m(sin ),P2m(sin ,-cos ,-cos ),P3m(-cos ),P3m(-cos ,-sin ,-sin ),P4m(-sin ),P4m(-sin ,cos ,cos ) (0 ) (0    /2m). Ekkor xm2+x2m2+x3m2+x4m2=2(sin2 /2m). Ekkor xm2+x2m2+x3m2+x4m2=2(sin2 +cos2 +cos2 )=ym2+y2m2+y3m2+y4m2=2(sin2 )=ym2+y2m2+y3m2+y4m2=2(sin2 +cos2 +cos2 )=2. Ezt eljátszva a többi átlópárral kapjuk, hogy n=4m esetén )=2. Ezt eljátszva a többi átlópárral kapjuk, hogy n=4m esetén 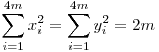 (0 (0    /2m). /2m).
n=2m esetén a problémát visszavezetjük az n=4m esetre: Töröljük a 4m-szög azon Pi csúcsait, ahol 2|i, ekkor kapunk egy szabályos 2m-szöget. Minden átlópár egyik tagja törölve lett a végpontokkal és azok koordinátáival együtt. Mivel xm2+x3m2=ym2+y3m2=x2m2+x4m2=y2m2+y4m2 és ez igaz minden átlópárra, azért 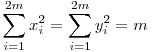 . .
n=m esetén a problémát visszavezetjük az n=2m esetre: Megintcsak töröljük a 2m-szög azon pi csúcsait, ahol 2|i, ekkor egy szabályos m szöget kapunk. Minden átló egyik végpontja törölve lett. Az átlók végpontjai az origóra tükrözve egymásba vihetők, ezért a koordinátáik egymás ellentettjei: Pi(xi,yi)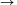 Pi'(-xi,-yi), vagyis xi2=(-xi)2, yi2=(-yi)2. Ebből már következik, hogy Pi'(-xi,-yi), vagyis xi2=(-xi)2, yi2=(-yi)2. Ebből már következik, hogy 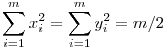 , m tetszőleges, tehát az állítás igaz bármely természetes számra. , m tetszőleges, tehát az állítás igaz bármely természetes számra.
|
| Előzmény: [647] jenei.attila, 2011-05-02 12:53:41 |
|
|





 10 és n-nek van 5-nél kisebb számjegye, akkor ott elvágjuk n-et és indukcióval teljesül az állítás n-re is. Így feltehető, hogy n minden jegye legalább 5, akkor minden helyiértéken van átvitel a szorzásnál, így a következő jegy a szorzatban nem lehet nulla, hiszen (2*d+1)mod 10 a jegy, ami páratlan, így nem nulla. Azaz L jegyű n esetén S(n)
10 és n-nek van 5-nél kisebb számjegye, akkor ott elvágjuk n-et és indukcióval teljesül az állítás n-re is. Így feltehető, hogy n minden jegye legalább 5, akkor minden helyiértéken van átvitel a szorzásnál, így a következő jegy a szorzatban nem lehet nulla, hiszen (2*d+1)mod 10 a jegy, ami páratlan, így nem nulla. Azaz L jegyű n esetén S(n) 9L (ez trivi), míg S(2n)
9L (ez trivi), míg S(2n)




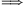 an(an-lc)=l-1>0. Ezért egyrészt an|l-1 és így an<l, másrészt an-lc>0, ebből pegig an>lc
an(an-lc)=l-1>0. Ezért egyrészt an|l-1 és így an<l, másrészt an-lc>0, ebből pegig an>lc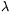 1,2 az x2-cx+1=0 egyenlet gyökei (
1,2 az x2-cx+1=0 egyenlet gyökei (

 /2m kikötés felesleges,
/2m kikötés felesleges,  N).
N).  Pi'(-xi,-yi), vagyis xi2=(-xi)2, yi2=(-yi)2. Ebből már következik, hogy
Pi'(-xi,-yi), vagyis xi2=(-xi)2, yi2=(-yi)2. Ebből már következik, hogy