| [711] m2mm | 2012-10-12 13:39:38 |
 Szándékos is lehetett, letesztelni ki az akit lehet tanítani, nem csak vegetál szakkörökön, illetve ki az aki a nehéznek tűnő feladatokat bemisztifikálja és esélytelen emiatt egy IMO 3 vagy 6-ra...
|
| Előzmény: [710] Róbert Gida, 2012-10-12 00:56:00 |
|
| [710] Róbert Gida | 2012-10-12 00:56:00 |
 Lejárt A567. megoldása.
Ritkán ad a szerkesztő (Kós Géza) segítséget egy akkor még élő feladathoz. Az olimpiai szakkör második feladatának (1988/6) megoldásában ugyanaz a trükk van, mint az egyébként pont a Pelikán által kitűzött A567-ben.
Egyszerre oldom meg az a,b, részét a feladatnak, legyen e=5 vagy 3. A feladat szerint a|b2-e, és b|a2-e és a,b relatív prímek, így ab|a2+b2-e is teljesül, sőt ez megfordítva is igaz (kivéve az, hogy relatív prímek lesznek). Nagyszerű, a két oszthatósági feltételből egyet csináltam.
Ha ab|a2+b2-e, akkor a2+b2-e=kab teljesül valamilyen k egészre (k lehet negatív is). Az a,b szerepe szimmetrikus, így feltehető, hogy a b. Rendezve: b2-kab+a2-e=0, azaz x=b megoldása az x2-kax+a2-e=0 másodfokú egyenletnek. Végtelen leszállás (méthode de descente infinie) következik, majd felszállás. b. Rendezve: b2-kab+a2-e=0, azaz x=b megoldása az x2-kax+a2-e=0 másodfokú egyenletnek. Végtelen leszállás (méthode de descente infinie) következik, majd felszállás.
Tegyük fel, hogy a>2 teljesül. Ha az egyenletnek az egyik megoldása 'b', akkor a másik b2=ka-b (gyökök és együtthatók közti összefüggés) és a,b2-re teljesül, hogy a2+b22-e=kab2, sőt a,b2 relatív prímek, hiszen lnko(a,b2)=lnko(a,ka-b)=lnko(a,b), továbbá b2 egész (trivi), és pozítiv, hiszen  , mert a2-e , mert a2-e 9-5=4>0 és b>0. Már csak az kell, hogy "kisebb" megoldást találtunk, valóban: 9-5=4>0 és b>0. Már csak az kell, hogy "kisebb" megoldást találtunk, valóban: 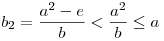 (utóbbi azért, mert a (utóbbi azért, mert a b volt). Azaz a (b2,a) pár megoldás, ahol b2<a, így az (a,b) párnál a rendezésben kisebb megoldást kaptunk. b volt). Azaz a (b2,a) pár megoldás, ahol b2<a, így az (a,b) párnál a rendezésben kisebb megoldást kaptunk.
Leszállás addig működik, amíg az a>2 feltétel teljesül. Mikor akadunk el e=3 esetben: ha a=1, akkor b=1 vagy b=2, míg az a=2 eset nem ad megoldást. Így (még a (2,1) páron kívül) nincs más megoldás, hiszen a felszálláshoz szükséges b>2 feltétel egyikre sem teljesül. Ha e=5, akkor a=1 esetén b=1,2,4 és a=2 nem ad megoldást. Végtelen felszállás működik, de csupán az (1,4) párra, hiszen ott b>2. Figyeljük meg, hogy k értéke egy sorozat mentén konstans, itt k=3. Azaz az összes megoldás (1,1),(1,2) és legyen a0=1;a1=4;an=3an-1-an-2, ekkor (an,an+1) megoldás, illetve ezek felcserélésével kapott párok. És nincs több megoldás. Ehhez még elsüthetjük azt, hogy a fel/leszállás adott megoldásból kiindulva egyértelmű, hiszen a másodfokú egyenletnek két gyöke van.
|
|
| [709] Róbert Gida | 2012-05-10 23:56:19 |
 Tavalyi B. 4364. megoldásához:
Legyen c=z;b=y+z;a=x+y+z ahol x,y,z nemnegatív a feltételek miatt. Behelyettesítve és rendezve az egyenlőtlenséget bal oldalra minden tag együtthatója pozitív lesz. Nagyon olcsó példa.
A Mathematica is bebizonyítja (Simplify elég hozzá).
|
|
| [708] Róbert Gida | 2012-04-11 17:11:59 |
 (lejárt) A557.
Solution. Define a1=3,an+1=(an2+1)/2. Paint the numbers in the interval Ai=[ai,ai+1) in the color i mod 3. The number 1 painted in color 2, number 2 - as you like. Now consider any x,y,z(x<y) such that x+y=z2 and z lies in Ai. Then it is easy to see that y is either Ai+1, or Ai+2, ie, y and z have different colors. Equality 1+3=22 is also not suitable.
A megoldás az internetről jön. Oroszból lefordítva a google translate segítségével (tex-be áttéve és a mat.jeleket újra beírva). 5 perc alatt találtam meg, google és google translate kellett hozzá. Kezdő internetezőnek talán érdekes lehet, hogy nulla orosz tudással egy orosz lapon levő zip-elt file-ban levő orosz nyelvű feladatot és megoldást miért is lehet egyáltalán megtalálni. Kömal kiírásból: "Többször előfordult már, hogy egy-egy feladat szerepelt valamely példatárban, vagy megtalálták az interneten...Célunk továbbra is versenyzőink problémamegoldó képességének feljesztése, nem pedig a keresőprogramok tesztelése", de itt nem pusztán kereső kellett hozzá. És ez nem az első Kolmogorov kupás feladat volt az A jelűek között, talán érdemes lenne kitűzés előtt az interneten rákeresni, hogy a megoldás fent van-e. Megjegyzem nem minden megoldást tettek fel a Kolmogorov kupáról, de például az A545 és az A539 Kolmogorov kupás feladatok megoldásai ugyanitt megtalálhatóak. 15 ingyen pont kicsit sok az A pontversenyben 1 tanév alatt, nem?
|
|
| [707] m2mm | 2012-04-11 13:47:52 |
 A. 558. feladatot valaki megoldotta a fórumosok közül? Érdekelne a megoldása.
|
|
| [706] nadorp | 2012-03-14 00:45:26 |
 2. megoldás az A556 feladatra:
Legyen 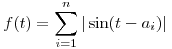 . Ha n=1, akkor t=a1 választással a feladat állítása nyilván teljesül, ezért a továbbiakban feltesszük, hogy n . Ha n=1, akkor t=a1 választással a feladat állítása nyilván teljesül, ezért a továbbiakban feltesszük, hogy n 2. 2.
Mivel az f(t) függvény  -szerint periodikus, ezért az állítást elegendő abban az esetben bizonyítani, amikor -szerint periodikus, ezért az állítást elegendő abban az esetben bizonyítani, amikor
0 t< t< és 0 és 0 ai< ai< ( 1 ( 1 i i n), sőt az általánosság megsértése nélkül az is feltehető, hogy n), sőt az általánosság megsértése nélkül az is feltehető, hogy
. Ekkor
| (2) | 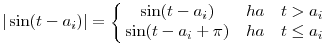 |
Szükségünk lesz még a következő azonosságra
| (3) |  |
Valóban
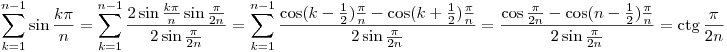
Rátérve a feladat bizonyítására, azt fogjuk belátni, hogy az (1) feltételek mellett 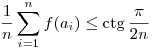 . Ebből már következik a feladat állítása, hiszen ha . Ebből már következik a feladat állítása, hiszen ha 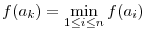 , akkor , akkor 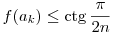 is teljesül. is teljesül.
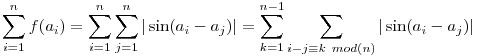
Itt felhasználva (2)-t és hogy a sinus függvény a [0, ] intervallumon konkáv ] intervallumon konkáv

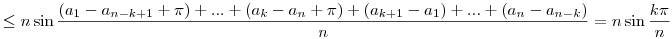
tehát (3) alapján
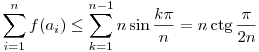
Megjegyzés: Az f(t) függvény minimumára adott felső becslés általában már nem javítható, ugyanis  (1 (1 k k n) esetén n) esetén 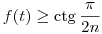 teljesül és egyenlőség t=ak+m teljesül és egyenlőség t=ak+m ( m egész) esetén van ( m egész) esetén van
|
|
| [705] jenei.attila | 2012-03-13 09:14:30 |
 Szép feladat volt ez, és nagyon szép megoldásokat adtatok rá. Különösen az első tetszett, de Fálasz Mihályé is igen elegáns. A harmadik a vektorok használatának erejét mutatja, az is nagyon ügyes. Grat mindkettőtöknek.
|
| Előzmény: [702] HoA, 2012-03-09 10:49:57 |
|
| [704] HoA | 2012-03-09 14:43:39 |
 A szemléletes megoldások után jöjjön egy mechanikus, vektoralgebrai. Jelöljük a 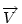 vektor 90 fokos pozitív elforgatottját vektor 90 fokos pozitív elforgatottját 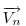 -nel, -nel, 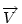 és és 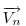 összegét összegét 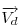 -vel . -vel . 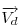 a a 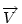 -vel 45 fokos szöget bezáró, -vel 45 fokos szöget bezáró,  hosszúságú vektor. Könnyen belátható, hogy tetszőleges hosszúságú vektor. Könnyen belátható, hogy tetszőleges 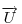 és és 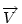 vektorokra vektorokra 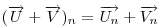
Legyen 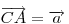 , , 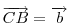 . Ekkor . Ekkor 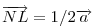 , , 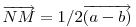 , , 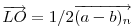 , , 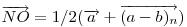 . Hasonlóan . Hasonlóan 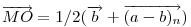
 . Mivel . Mivel 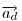 és és 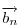 adott hosszúságú vektorok, különbségük abszolút értéke akkor lesz a legnagyobb, ha egy egyenesbe esnek és ellentétes irányúak. adott hosszúságú vektorok, különbségük abszolút értéke akkor lesz a legnagyobb, ha egy egyenesbe esnek és ellentétes irányúak. 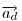 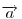 - hoz képest 45 fokra áll, tehát - hoz képest 45 fokra áll, tehát 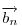 225 fokra és így 225 fokra és így 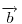 135 fokra. Hasonlóan adódik, hogy 135 fokra. Hasonlóan adódik, hogy 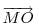 is akkor a leghosszabb, ha is akkor a leghosszabb, ha 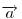 és és 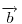 135 fokos szöget zár be. 135 fokos szöget zár be.
|
| Előzmény: [703] Fálesz Mihály, 2012-03-09 13:37:29 |
|
| [703] Fálesz Mihály | 2012-03-09 13:37:29 |
 B. 4408. Az ABC háromszögben AC és BC oldalak hossza rögzített, a C-nél levő szög pedig változik. Az AC oldal felezőpontja M, a BC oldal felezőpontja N, az AB oldalra kifelé állított négyzet középpontja pedig O. Hogyan kell az ACB szöget megválasztani ahhoz, hogy az OM és ON távolságok összege a lehető legnagyobb legyen?
Megoldás. Legyen az AB oldal felezőpontja K, ekkor persze CMKN paralelogramma, és megjelölt szögek egyállású szögek. Az AOK és BOK háromszögek egyenlő szárú derékszögű háromszögek.
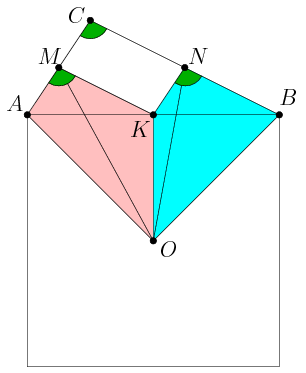
Írjuk fel a Ptolemaiosz-tétel egyenlőtlenség alakját az OAMK négyszögre: OM.AK OA.MK+OK.AM; ebből OA.MK+OK.AM; ebből
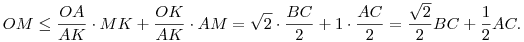 | (1) |
Egyenlőség akkor van, ha OAMK húrnégyszög. Mivel AOK =45o, ez ekvivalens azzal, ha KMA =45o, ez ekvivalens azzal, ha KMA =135o, azaz BCA =135o, azaz BCA =135o. =135o.
Ha a Ptolemaiosz-tételt az OBNK négyszögre írjuk fel, akkor azt kaphatjuk, hogy
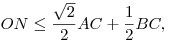 | (2) |
és egyenlőség most is akkor van, ha BCA =135o. =135o.
Az (1) és (2) becslések összeadásával
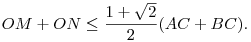
Az OM és ON összege tehát legfeljebb 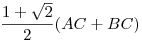 , és ez az érték akkor áll elő, ha BCA , és ez az érték akkor áll elő, ha BCA =135o. =135o.
|
| Előzmény: [702] HoA, 2012-03-09 10:49:57 |
|
| [702] HoA | 2012-03-09 10:49:57 |
 B. 4408. Az ABC háromszögben AC és BC oldalak hossza rögzített, a C-nél levő szög pedig változik. Az AC oldal felezőpontja M, a BC oldal felezőpontja N, az AB oldalra kifelé állított négyzet középpontja pedig O. Hogyan kell az ACB szöget megválasztani ahhoz, hogy az OM és ON távolságok összege a lehető legnagyobb legyen?
Az 1. ábrán MNPQ és ABRS négyzetek, L az AB oldal felezőpontja. 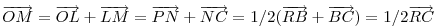 és hasonlóan és hasonlóan 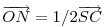 Így feladatunkkal egyenértékú, ha az RC és SC távolságok összegének maximumát keressük, ahol ABRS az AB oldalra kifelé állított négyzet. Így feladatunkkal egyenértékú, ha az RC és SC távolságok összegének maximumát keressük, ahol ABRS az AB oldalra kifelé állított négyzet.
Rögzítsük a háromszög AC oldalát. ( 2. ábra ) Ekkor B a C körüli r1=a sugarú k1köríven mozoghat, 90 fokos C-nél levő szöghöz tartozó helyzete legyen B0 , egy másik helyzete B1 . Legyen ACGH az AC egyenes B0 -t tartalmazó olalán állított négyzet. S-et úgy kapjuk, hogy B-t A körül óramutató járás irányában ( negatív irány ) 90 fokkal elfordítjuk, S rajta van a H középpontú a sugarú k2 körön, B0-nak ill. B1 -nek megfelelő helyzete S0 ill. S1 . R-et B-nek A körüli 45 fokos  nagyítású nyújtva forgatásával kapjuk, R rajta van a G középpontú nagyítású nyújtva forgatásával kapjuk, R rajta van a G középpontú 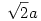 sugarú k3 körön, B0-nak ill. B1 -nek megfelelő helyzete R0 ill. R1 . RC akkor a leghosszabb, ha R k3 és a CG egyenes R* metszéspontjába kerül. Ekkor R0GR* szög 45 fokos, ez B-nek arra a B* helyzetére fordul elő, ha a B0CB* szög 45 fokos, vagyis az ACB szög 135 fokos. Hasonlóan SC akkor a leghosszabb, ha S k2 és a CH egyenes S* metszéspontjába kerül. Ekkor S0HS* szög 45 fokos, tehát SC is akkor a leghosszabb, ha B B* -ban van. Ezért az RC és SC távolságok összegének maximuma az ACB szög 135 fokos értékénél adódik. Ez a maximális távolságösszeg az ábrából leolvashatóan sugarú k3 körön, B0-nak ill. B1 -nek megfelelő helyzete R0 ill. R1 . RC akkor a leghosszabb, ha R k3 és a CG egyenes R* metszéspontjába kerül. Ekkor R0GR* szög 45 fokos, ez B-nek arra a B* helyzetére fordul elő, ha a B0CB* szög 45 fokos, vagyis az ACB szög 135 fokos. Hasonlóan SC akkor a leghosszabb, ha S k2 és a CH egyenes S* metszéspontjába kerül. Ekkor S0HS* szög 45 fokos, tehát SC is akkor a leghosszabb, ha B B* -ban van. Ezért az RC és SC távolságok összegének maximuma az ACB szög 135 fokos értékénél adódik. Ez a maximális távolságösszeg az ábrából leolvashatóan 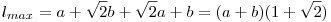 . Eredeti feladatunk maximális távolságösszege ennek a fele. . Eredeti feladatunk maximális távolságösszege ennek a fele.
|
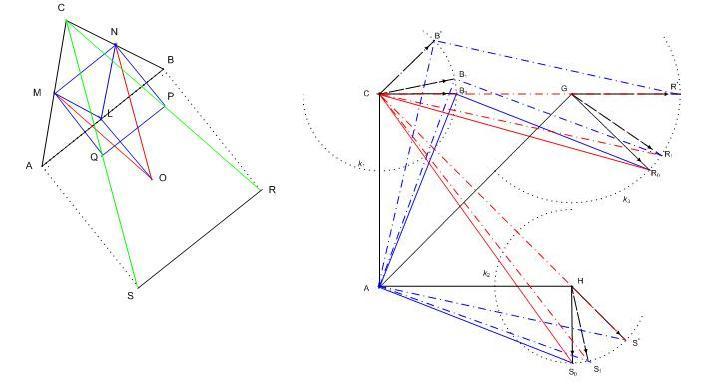 |
| Előzmény: [701] elrond16, 2012-02-27 16:33:37 |
|
| [701] elrond16 | 2012-02-27 16:33:37 |
 Sziasztok!
Engem nagyon erdekelne a B.4408-as feladat megoldasa. Ha esetleg valaki beirna, vagy elkuldene nekem a megoldasat nagyon orulnek! Koszi
|
|
|
| [699] Fálesz Mihály | 2012-02-14 23:31:01 |
 Az A.545. megoldása két becslésből áll:
![\frac{a^2-b^2}2 \le [a+b,a-b] \le b^2-1.](keplet.cgi?k=E4996BEF56045EC1)
Mindkét egyenlőtlenség onnan jött, hogy a kisebbik szám osztója a nagyobbiknak. Ha valamelyik esetben nincs egyenlőség, akkor az arány legalább 2, és az is igaz, hogy a2-b2 b2-1. b2-1.
|
| Előzmény: [697] Róbert Gida, 2012-02-14 17:46:12 |
|
|
| [697] Róbert Gida | 2012-02-14 17:46:12 |
 Hát nem látható. Két feladatot összetéve: 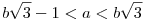 , illetve még azt is bizonyította, hogy a2 , illetve még azt is bizonyította, hogy a2 3b2-2, de még ezekből sem következik, hogy a2=3b2-2 lehet csak. 3b2-2, de még ezekből sem következik, hogy a2=3b2-2 lehet csak.
De valóban kijön egy kis munkával: A545. megoldásából: b2-1 többese [a+b,a-b]-nek, így alkalmas pozitív g egésszel: b2-1=g*[a+b,a-b], továbbá (a+b,a-b)=2 miatt az is igaz, hogy ![[a+b,a-b]=\frac {a^2-b^2}{e}](keplet.cgi?k=C3AABA8414CF0938) . Azaz a kettő egyenletből: . Azaz a kettő egyenletből: 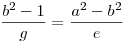 . Itt e=1,2 lehet csupán A545 szerint. . Itt e=1,2 lehet csupán A545 szerint.
e=1 esetén kapjuk: b2-1=g(a2-b2), ebből: 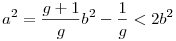 , amiből: , amiből: 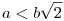 , ami ellentmondás lesz , ami ellentmondás lesz 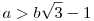 -gyel, ha b>3. -gyel, ha b>3.
e=2-nél hasonlóan, 2(b2-1)=g(a2-b2), amiből: 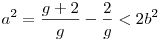 , ha g>1, ami megint ellentmondás. Ha g=1, akkor meg 2(b2-1)=a2-b2, azaz a2-3b2=-2, és pont ezt kellett bizonyítani. (A551 miatt ez mindig megoldás). , ha g>1, ami megint ellentmondás. Ha g=1, akkor meg 2(b2-1)=a2-b2, azaz a2-3b2=-2, és pont ezt kellett bizonyítani. (A551 miatt ez mindig megoldás).
A végtelen leszállást meg úgy értettem, hogy a feladatot végtelen leszállással bizonyítsuk be, hogy még az is kijöjjön, hogy nincs más megoldás.
|
| Előzmény: [696] Fálesz Mihály, 2012-02-14 09:21:43 |
|
|
| [695] Róbert Gida | 2012-02-14 01:48:18 |
 Azt senki nem gondolta végig, hogy a megadottakon kívül miért nincs más megoldás? Egy lehetséges út lenne végtelen leszállást alkalmazni, voltak hasonló olimpiai példák is. Itt nem látom, hogy lehetne ilyet csinálni, ráadásul itt két oszthatósági feltétel is van.
|
| Előzmény: [694] Róbert Gida, 2012-02-11 12:48:17 |
|
| [694] Róbert Gida | 2012-02-11 12:48:17 |
 Lejárt A551. megoldása:
Az ezer alatti megoldások géppel könnyen megkaphatóak, ezek: (5,3),(19,11),(71,41),(265,153),(989,571). Tehát az "a", illetve "b" sorozat: 5,19,71,265,989 és 3,11,41,153,571 Ezek a sorozatok Neil Sloane adatbázisában benne vannak (előkelő helyen): A001834 és A001835. Én legalábbis nem lepődök meg, hogy a Pell egyenletekhez van közük a sorozatoknak, de az ismert tételeket a Pellből nem fogom használni.
(a*b+1)/(a+b) és (a*b-1)/(a-b) (egész elemű) sorozatra is érdemes rákeresni, ez valójában egy sorozat: A001075. Az explicit képleteket is megadja Neil, ezeket használom:
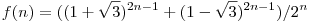
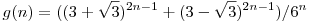
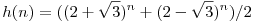
Pell helyett: megfelelő lineáris rekurziót teljesítik a sorozatok (kezdőtagok is jók), így a sorozat tagjai egész számok (ez karakterisztikus polinomokkal is kijön). Legyen a=f(n) és b=g(n). Ekkor bizonyítható a képlettel, hogy a2-3*b2=-2, ebből pedig 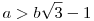 . .
a*b+1=(a+b)*h(n-1)
a*b-1=(a-b)*h(n)
is teljesül, ezeket is az explicit képlettel láthatjuk be, ehhez célszerű minden tagot s*tn alakban felírni. Ami kellett (az (f(n),g(n)) számpárok különbözőek, így ez végtelen sok megoldást ad).
|
|
| [693] m2mm | 2012-01-18 22:18:11 |
 A.549. (Többször elég vázlatos lesz)
Lemma: UVW háromszög VW oldal belső P pontjára tekintsük UVP és UPW háromszögek O1, O2 középpontú beírt köreit, e két kör közös belső érintője nyilván UP. Ekkor a másik közös belső érintő VW oldalt a beírt kör E érintési pontjában metszi(ha a két kör érinti egymást, akkor a két belső érintő egybeesik, ezesetben ez megy át a kérdéses ponton).
Ez könnyen bizonyítható csupán az érintőszakaszok felírásával, ezt most nem részletezem.
Innen az érintő egyenesek miatt adódik egyszerűen, hogy O1PO2 =90°=O1EO2 =90°=O1EO2 , azaz O1O2PE húrnégyszög. , azaz O1O2PE húrnégyszög.
Mivel ABCD érintőnégyszög, ezért ABC és CDA beírt körei AC-t egy pontban érintik (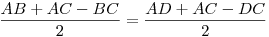 , mivel AB+DC=AD+CB), mondjuk F-ben. , mivel AB+DC=AD+CB), mondjuk F-ben.
Legyen ABE, BCE, CDE, DAE háromszögek beírt köreinek középpontja rendre O1,O2,O3,O4. Előbbiekből jön, hogy O1O2EF és O3O4EF húrnégyszögek.
Van az az eset, amikor E,F egybeesik, de ekkor kisakkozható, hogy ABC és CDA beírt körei érintik egymást, azaz ami a lényeg és megjegyezzük, hogy O1O2E és O3O4E körök hatványvonala AC.
Monge szerint(három hasonlósági pont tétele...) ABD és BCD háromszögek beírt köreinek külső hasonlósági K pontja AC-re illeszkedik, ha a harmadik körnek ABCD beírt körét vesszük.(két külső hasonlósági pont a háromból A és C...) ABD beírt körének középpontja nyilván BO1-en rajta van(belső szögfelezője ABD-nek...) és hasonlóan BDC beírt körének középpontja BO2-n. Mivel a belső hasonlósági pont közös belső érintőn van, továbbá két kör kp-ja és hasonlósági pontjai harmonikus pontnégyes + van egy Papposz-Steinerünk, ezért BO1,BE,BO2 egyeneseket tekintve BE harmonikus társa BK.
De ABE és BEC beírt köreinek középpontja és hasonlósági pontjai is harmonikust hat. meg, így e két kör R külső hasonlósági pontjára BR BE-nek harmonikus társa BO1,BO2,BE tekintetében. Mivel R és K nyilván AC-n van, így ebből az adódik, hogy R=K.
Ezt eljátszva O3,O4-re az adódik, hogy O1O2 és O3O4 R-ben metszik egymást, ergo AC-n. Mivel AC hatványvonala volt két körünknek anno, így innen triviális a húrnégyszögség.
|
|
| [692] Róbert Gida | 2012-01-12 16:33:32 |
 http://www.komal.hu/verseny/feladat.cgi?a=feladat&f=A550&l=hu azt hiszem az én megoldásom az egyszerűbb. A hivatalos megoldást végigszámolva a kínai 5093338546785390*k+1400926917841815 sorozatot nézi, míg én a 38*k+21 számtani sorozatot.
|
| Előzmény: [691] Róbert Gida, 2012-01-11 14:15:23 |
|
| [691] Róbert Gida | 2012-01-11 14:15:23 |
 Lejárt A550. megoldása: Teljesen trivi becsléssel nem jön ki: nézzük meg hány szám áll elő n-ig! n-ig van legfeljebb 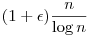 prím és prím és 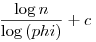 Fibonacci szám, ahol Fibonacci szám, ahol 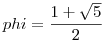 . Így n-ig van kb. . Így n-ig van kb. 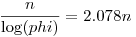 darab nem feltétlenül különböző előállítás (ez azért igaz, mert ugyan a prímek viszonylag sűrűn vannak, de a Fibonacci számok már ritkán.) Itt darab nem feltétlenül különböző előállítás (ez azért igaz, mert ugyan a prímek viszonylag sűrűn vannak, de a Fibonacci számok már ritkán.) Itt 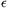 >0 tetszőlegesen kicsinek választható, ha n nagy, illetve c (korlátos) konstans. Ez a becslés viszont már mutatja, hogy az állítás valószínűleg hamis lesz. >0 tetszőlegesen kicsinek választható, ha n nagy, illetve c (korlátos) konstans. Ez a becslés viszont már mutatja, hogy az állítás valószínűleg hamis lesz.
Amiben reménykedhetünk, hogy egy adott maradékosztálynál már kevés előállítás van. Itt a sűrűséget ki tudjuk számolni: Fibonacci számok m-mel vett osztási maradéka periodikus, a prímeké ugyan nem, de ott van a számtani sorozatok prímszámtétele (nagyágyú): ha gcd(r,m)=1, akkor a prímek 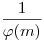 -ed részére p -ed részére p r mod m. Ha r és m nem relatív prím, akkor legfeljebb egy ilyen prím van. r mod m. Ha r és m nem relatív prím, akkor legfeljebb egy ilyen prím van.
Géppel: m=34;r=17 a legkisebb jó választás! Nézzünk egy másikat amit bizonyítok: m=38;r=21, ekkor a Fibonacci számok periodikusak mod 38, és a periódus 18. Tekintsük a fibonacci(i)+p=38k+21 n megoldásszámát, ahol p prím. i mod 18 szerint nézzük az egyenletet. Ekkor az i választható n megoldásszámát, ahol p prím. i mod 18 szerint nézzük az egyenletet. Ekkor az i választható 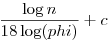 -nek, ha i mod 18 rögzített, akkor p -nek, ha i mod 18 rögzített, akkor p 21-fibonacci(i) mod 38. Számtani sorozatokra vonatkozó prímszámtételből tudjuk, hogy hány ilyen prím van n-ig. 21-fibonacci(i) mod 38. Számtani sorozatokra vonatkozó prímszámtételből tudjuk, hogy hány ilyen prím van n-ig.
Kapjuk a megoldásszámra (felső) becslést: 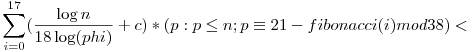 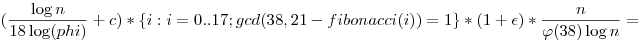 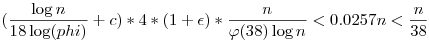 , ami kellett. (Többit az olvasóra bízom. Ezt még ki kéne rendesen epszilonozni , illetve még belevenni azon maradékosztályokat, ahol legfeljebb egy prím van, de ez már nem változtat sokat az előállítások számán.) , ami kellett. (Többit az olvasóra bízom. Ezt még ki kéne rendesen epszilonozni , illetve még belevenni azon maradékosztályokat, ahol legfeljebb egy prím van, de ez már nem változtat sokat az előállítások számán.)
|
|
| [690] m2mm | 2011-12-03 13:41:44 |
 B. 4380. m=0 esetén n függvényében legfeljebb mennyi lehet az egyenlő hosszú szakaszok száma?
|
|
|
|
| [687] Róbert Gida | 2011-11-15 16:49:29 |
 Lejárt októberi A542. hivatalos megoldásához: a hamis érem megnevezésének is determinisztikusnak kell lennie, mert előfordulhat, hogy egyszerre több hamis érmét is találunk. Továbbá a kiegészítések igenekkel elhagyhatóak, elég annyi, hogy a játékfának max. 512 levele lesz a legfeljebb 9 kérdés után.
|
|




 b. Rendezve: b2-kab+a2-e=0, azaz x=b megoldása az x2-kax+a2-e=0 másodfokú egyenletnek. Végtelen leszállás (méthode de descente infinie) következik, majd felszállás.
b. Rendezve: b2-kab+a2-e=0, azaz x=b megoldása az x2-kax+a2-e=0 másodfokú egyenletnek. Végtelen leszállás (méthode de descente infinie) következik, majd felszállás.  9-5=4>0 és b>0. Már csak az kell, hogy "kisebb" megoldást találtunk, valóban:
9-5=4>0 és b>0. Már csak az kell, hogy "kisebb" megoldást találtunk, valóban:  -szerint periodikus, ezért az állítást elegendő abban az esetben bizonyítani, amikor
-szerint periodikus, ezért az állítást elegendő abban az esetben bizonyítani, amikor 


 =45o, ez ekvivalens azzal, ha KMA
=45o, ez ekvivalens azzal, ha KMA
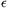 >0 tetszőlegesen kicsinek választható, ha n nagy, illetve c (korlátos) konstans. Ez a becslés viszont már mutatja, hogy az állítás valószínűleg hamis lesz.
>0 tetszőlegesen kicsinek választható, ha n nagy, illetve c (korlátos) konstans. Ez a becslés viszont már mutatja, hogy az állítás valószínűleg hamis lesz.  r mod m. Ha r és m nem relatív prím, akkor legfeljebb egy ilyen prím van.
r mod m. Ha r és m nem relatív prím, akkor legfeljebb egy ilyen prím van.