| [728] w | 2012-11-24 19:47:44 |
 Több pont általánosításokra? Jó lehetett. Persze, annak is van értelme, hogy nincs extra pont, pl. a B-ben könnyebb egy egyszerűbb példát általánosítani, mint egy összetettebb példa megoldásával megszerezni ugyanazt a pontszámot. Én mondjuk ennek ismeretében mégis hozzáírom a megjegyzéseket, mert szerintem érdemes a javítóval tudatni, hogy a példát kissé továbbgondoltam. Kevés időt vesz igénybe, nem sülhet ki rosszul, és hát nem érzem úgy, hogy "hiányos" a dolgozat.
|
| Előzmény: [727] Róbert Gida, 2012-11-24 15:46:52 |
|
| [727] Róbert Gida | 2012-11-24 15:46:52 |
 "Természetesen lehet általánosítani, Megjegyzés rovatba :)"
Igen, de nem kapsz rá plusz pontot. Ami nagyon is jól van, a mi időnkben még volt olyan, hogy valaki az eredetileg 5 pontos feladatra általánosítások miatt 8 pontot kapott.
|
| Előzmény: [726] w, 2012-11-24 12:34:57 |
|
| [726] w | 2012-11-24 12:34:57 |
 Szerintem azért így tűzték ki a feladatot, mert ilyen formában nehezebb rájönni a megoldásra, első nekifogásban valamilyen egyszerű módszerrel (szögszámítás, Thálesz, Pit.) állok hozzá (magam nevében beszélek). Több adattal több felesleges dolog jön ki, amibe belegabalyodhatok. Végül egyszerűen kijött, Apollóniusz-körrel. Természetesen lehet általánosítani, Megjegyzés rovatba :)
|
|
| [725] m2mm | 2012-11-23 16:28:38 |
 Ha A,B,C,D pontok ilyen sorrendben egy egyenesen vannak és harmonikus pontnégyest határoznak meg, akkor tetszőleges I pontra a síkon(leszámítva AB egyenes pontjait), pontosan akkor lesz 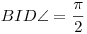 , ha AIB , ha AIB =BIC =BIC . Ez belátható pl. szinusz-tételekkel, ujjgyakorlat. . Ez belátható pl. szinusz-tételekkel, ujjgyakorlat.
Így valójában a feladatban P lehet bármely mást pont AB oldalon és Q az AP.BQ=AQ.BP feltétellel megadott pont(AB egyenesen), akkor is fennáll a szögfelező tulajdonság, magyarán van egy kis fölös információ a feladatban.
|
| Előzmény: [723] Erben Péter, 2012-11-23 10:24:07 |
|
|
| [723] Erben Péter | 2012-11-23 10:24:07 |
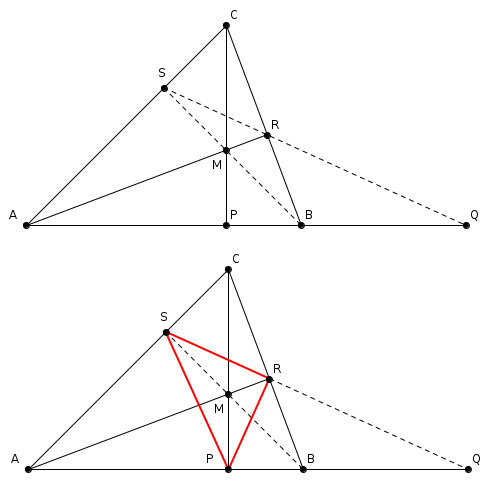
 Egy észrevétel a B.4477. egy lehetséges hátteréről.
A AP.BQ=AQ.BP feltétel így is írható:  . Erről - ha a pontok lehetséges sorrendjét elemezve a szakaszokat előjeles hosszal jellemezzük - a kettősviszony juthat eszünkbe: (ABPQ)=-1. . Erről - ha a pontok lehetséges sorrendjét elemezve a szakaszokat előjeles hosszal jellemezzük - a kettősviszony juthat eszünkbe: (ABPQ)=-1.
Tehát A és B harmonikusan választja el P-t és Q-t, amiből az következik, hogy Q az ábrán látható módon (szaggatott vonalak) szerkeszthető. (Az MRCS négyszög szemközti oldalegyeneseinek metszéspontja A és B, átlói pedig a P és Q pontokban metszik az AB egyenest.)
Végül arra kell csak emlékezni, hogy a PRS talpponti háromszög belső szögfelezői az ABC háromszög magasságvonalai, innen egyszerűen következik az eredeti feladat állítása.
|
 |
|
|
|
|
|
|
|
| [716] m2mm | 2012-11-14 00:43:58 |
 A.570. (vázlatos)
AC1(P)PB1(P) pontosan akkor érintőnégyszög, ha AB-AC=PB-PC(ismert, de érintőszakaszok felírásával triviális). P tehát az a pont, amin áthaladnak azon hiperbolaágak, melyekhez tartozó fókuszpontok ABC háromszög két csúcsa, és áthaladnak a harmadik csúcson. P megvan konstruálva, szerkesztés az már csúnyább, de a hiperbolaágak egyenlete felírható és ezekből a metszéspont is megvan... A kérdés, hogy számolás nélkül valaki megtudja-e szerkeszteni?
|
|
| [715] m2mm | 2012-11-14 00:18:15 |
 Hát na ne már egy egyenlőtlenség-feladat nem attól lesz szép, hogy kipróbálunk egy Cauchy-t és hopp, kijön belőle még egy lépéssel, hanem inkább tudatosan keressünk köztes becslést(mint a hiv. megoldás is) illetve a kifejezés, mint fv. viselkedéséből szűrünk le infót. Persze ez gusztus dolga.
Ja, az első egyenlőtlenségedben a két gyökös kifejezést nem összeadod, hanem összeszorzod, erre figyeljünk, az ember ebben hiába keres Cauchy-t.
|
| Előzmény: [714] valaki akit úgyis ismersz, 2012-11-13 22:07:01 |
|
| [714] valaki akit úgyis ismersz | 2012-11-13 22:07:01 |
 A szépség a feladatban az, hogy egyszerű módon is megoldható, ráadásul durva becslésekkel. Cauchy-egyenlőtlenség szerint 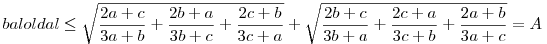 . .
Továbbá pl.
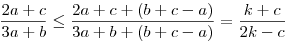
,ahol k=a+b+c (törtek becslésére vonatkozó tétel, 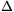 -egyenlőtlenség). Tehát -egyenlőtlenség). Tehát
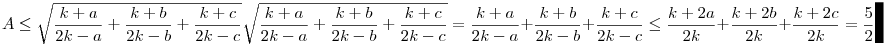 . .
Azaz készen vagyunk. A korlát élességéről némi határértékszámítással győződhetünk meg, ha a=b és c egészen kicsi.
|
|
| [713] nadorp | 2012-11-13 15:54:42 |
 A bizonyítás első része deriválás nélkül is megy:
(2a+c)(2b+c)=c2+2ac+2bc+4ab=(a+b+c)2-(a-b)2
(3a+b)(3b+a)=3a2+10ab+3b2=4(a+b)2-(a-b)2
Tehát, felhasználva, hogy 2(a+b)>a+b+c
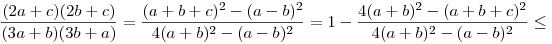
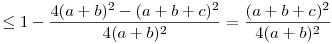
|
| Előzmény: [712] m2mm, 2012-11-13 13:42:08 |
|
| [712] m2mm | 2012-11-13 13:42:08 |
 A.571.
Először 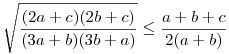 -t látom be. Négyzetre emelve és egy oldalra hozva a c-t tartalmazó tényezőket az ekvivalens -t látom be. Négyzetre emelve és egy oldalra hozva a c-t tartalmazó tényezőket az ekvivalens 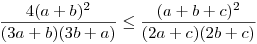 (*) a bizonyítandó. Rögzített 0<a,b-re tekintsük fa,b: R+->R+ (*) a bizonyítandó. Rögzített 0<a,b-re tekintsük fa,b: R+->R+ 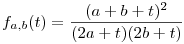 függvényt. függvényt.
 , mivel ez ekvivalens 2(a+b+t)(2a+t)(2b+t)-2(a+b+t)2(a+b+t) , mivel ez ekvivalens 2(a+b+t)(2a+t)(2b+t)-2(a+b+t)2(a+b+t) 0-val, (2a+t)(2b+t) 0-val, (2a+t)(2b+t) (a+b+t)2-tel, 0 (a+b+t)2-tel, 0 (a-b)2-tel. Tehát fa,b monoton csökkenő, továbbá a+b>c, így fa,b(c) (a-b)2-tel. Tehát fa,b monoton csökkenő, továbbá a+b>c, így fa,b(c) fa,b(a+b). Behelyettesítve (*) adódik. Tehát fa,b(a+b). Behelyettesítve (*) adódik. Tehát 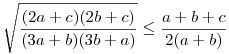 . A másik két tagra is felírva a hasonlóan adódó egyenlőtlenséget . A másik két tagra is felírva a hasonlóan adódó egyenlőtlenséget
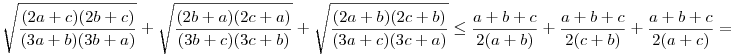
 , mivel , mivel 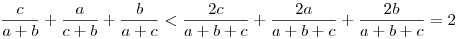 . .
|
|
| [711] m2mm | 2012-10-12 13:39:38 |
 Szándékos is lehetett, letesztelni ki az akit lehet tanítani, nem csak vegetál szakkörökön, illetve ki az aki a nehéznek tűnő feladatokat bemisztifikálja és esélytelen emiatt egy IMO 3 vagy 6-ra...
|
| Előzmény: [710] Róbert Gida, 2012-10-12 00:56:00 |
|
| [710] Róbert Gida | 2012-10-12 00:56:00 |
 Lejárt A567. megoldása.
Ritkán ad a szerkesztő (Kós Géza) segítséget egy akkor még élő feladathoz. Az olimpiai szakkör második feladatának (1988/6) megoldásában ugyanaz a trükk van, mint az egyébként pont a Pelikán által kitűzött A567-ben.
Egyszerre oldom meg az a,b, részét a feladatnak, legyen e=5 vagy 3. A feladat szerint a|b2-e, és b|a2-e és a,b relatív prímek, így ab|a2+b2-e is teljesül, sőt ez megfordítva is igaz (kivéve az, hogy relatív prímek lesznek). Nagyszerű, a két oszthatósági feltételből egyet csináltam.
Ha ab|a2+b2-e, akkor a2+b2-e=kab teljesül valamilyen k egészre (k lehet negatív is). Az a,b szerepe szimmetrikus, így feltehető, hogy a b. Rendezve: b2-kab+a2-e=0, azaz x=b megoldása az x2-kax+a2-e=0 másodfokú egyenletnek. Végtelen leszállás (méthode de descente infinie) következik, majd felszállás. b. Rendezve: b2-kab+a2-e=0, azaz x=b megoldása az x2-kax+a2-e=0 másodfokú egyenletnek. Végtelen leszállás (méthode de descente infinie) következik, majd felszállás.
Tegyük fel, hogy a>2 teljesül. Ha az egyenletnek az egyik megoldása 'b', akkor a másik b2=ka-b (gyökök és együtthatók közti összefüggés) és a,b2-re teljesül, hogy a2+b22-e=kab2, sőt a,b2 relatív prímek, hiszen lnko(a,b2)=lnko(a,ka-b)=lnko(a,b), továbbá b2 egész (trivi), és pozítiv, hiszen  , mert a2-e , mert a2-e 9-5=4>0 és b>0. Már csak az kell, hogy "kisebb" megoldást találtunk, valóban: 9-5=4>0 és b>0. Már csak az kell, hogy "kisebb" megoldást találtunk, valóban: 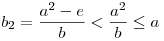 (utóbbi azért, mert a (utóbbi azért, mert a b volt). Azaz a (b2,a) pár megoldás, ahol b2<a, így az (a,b) párnál a rendezésben kisebb megoldást kaptunk. b volt). Azaz a (b2,a) pár megoldás, ahol b2<a, így az (a,b) párnál a rendezésben kisebb megoldást kaptunk.
Leszállás addig működik, amíg az a>2 feltétel teljesül. Mikor akadunk el e=3 esetben: ha a=1, akkor b=1 vagy b=2, míg az a=2 eset nem ad megoldást. Így (még a (2,1) páron kívül) nincs más megoldás, hiszen a felszálláshoz szükséges b>2 feltétel egyikre sem teljesül. Ha e=5, akkor a=1 esetén b=1,2,4 és a=2 nem ad megoldást. Végtelen felszállás működik, de csupán az (1,4) párra, hiszen ott b>2. Figyeljük meg, hogy k értéke egy sorozat mentén konstans, itt k=3. Azaz az összes megoldás (1,1),(1,2) és legyen a0=1;a1=4;an=3an-1-an-2, ekkor (an,an+1) megoldás, illetve ezek felcserélésével kapott párok. És nincs több megoldás. Ehhez még elsüthetjük azt, hogy a fel/leszállás adott megoldásból kiindulva egyértelmű, hiszen a másodfokú egyenletnek két gyöke van.
|
|
| [709] Róbert Gida | 2012-05-10 23:56:19 |
 Tavalyi B. 4364. megoldásához:
Legyen c=z;b=y+z;a=x+y+z ahol x,y,z nemnegatív a feltételek miatt. Behelyettesítve és rendezve az egyenlőtlenséget bal oldalra minden tag együtthatója pozitív lesz. Nagyon olcsó példa.
A Mathematica is bebizonyítja (Simplify elég hozzá).
|
|
| [708] Róbert Gida | 2012-04-11 17:11:59 |
 (lejárt) A557.
Solution. Define a1=3,an+1=(an2+1)/2. Paint the numbers in the interval Ai=[ai,ai+1) in the color i mod 3. The number 1 painted in color 2, number 2 - as you like. Now consider any x,y,z(x<y) such that x+y=z2 and z lies in Ai. Then it is easy to see that y is either Ai+1, or Ai+2, ie, y and z have different colors. Equality 1+3=22 is also not suitable.
A megoldás az internetről jön. Oroszból lefordítva a google translate segítségével (tex-be áttéve és a mat.jeleket újra beírva). 5 perc alatt találtam meg, google és google translate kellett hozzá. Kezdő internetezőnek talán érdekes lehet, hogy nulla orosz tudással egy orosz lapon levő zip-elt file-ban levő orosz nyelvű feladatot és megoldást miért is lehet egyáltalán megtalálni. Kömal kiírásból: "Többször előfordult már, hogy egy-egy feladat szerepelt valamely példatárban, vagy megtalálták az interneten...Célunk továbbra is versenyzőink problémamegoldó képességének feljesztése, nem pedig a keresőprogramok tesztelése", de itt nem pusztán kereső kellett hozzá. És ez nem az első Kolmogorov kupás feladat volt az A jelűek között, talán érdemes lenne kitűzés előtt az interneten rákeresni, hogy a megoldás fent van-e. Megjegyzem nem minden megoldást tettek fel a Kolmogorov kupáról, de például az A545 és az A539 Kolmogorov kupás feladatok megoldásai ugyanitt megtalálhatóak. 15 ingyen pont kicsit sok az A pontversenyben 1 tanév alatt, nem?
|
|
| [707] m2mm | 2012-04-11 13:47:52 |
 A. 558. feladatot valaki megoldotta a fórumosok közül? Érdekelne a megoldása.
|
|
| [706] nadorp | 2012-03-14 00:45:26 |
 2. megoldás az A556 feladatra:
Legyen 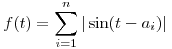 . Ha n=1, akkor t=a1 választással a feladat állítása nyilván teljesül, ezért a továbbiakban feltesszük, hogy n . Ha n=1, akkor t=a1 választással a feladat állítása nyilván teljesül, ezért a továbbiakban feltesszük, hogy n 2. 2.
Mivel az f(t) függvény  -szerint periodikus, ezért az állítást elegendő abban az esetben bizonyítani, amikor -szerint periodikus, ezért az állítást elegendő abban az esetben bizonyítani, amikor
0 t< t< és 0 és 0 ai< ai< ( 1 ( 1 i i n), sőt az általánosság megsértése nélkül az is feltehető, hogy n), sőt az általánosság megsértése nélkül az is feltehető, hogy
. Ekkor
| (2) | 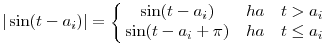 |
Szükségünk lesz még a következő azonosságra
| (3) |  |
Valóban
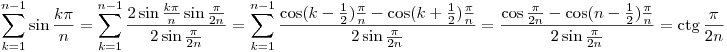
Rátérve a feladat bizonyítására, azt fogjuk belátni, hogy az (1) feltételek mellett 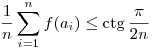 . Ebből már következik a feladat állítása, hiszen ha . Ebből már következik a feladat állítása, hiszen ha 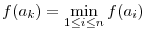 , akkor , akkor 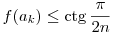 is teljesül. is teljesül.
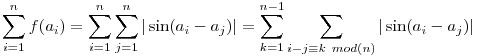
Itt felhasználva (2)-t és hogy a sinus függvény a [0, ] intervallumon konkáv ] intervallumon konkáv

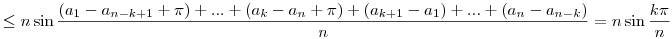
tehát (3) alapján
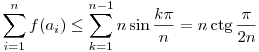
Megjegyzés: Az f(t) függvény minimumára adott felső becslés általában már nem javítható, ugyanis  (1 (1 k k n) esetén n) esetén 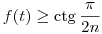 teljesül és egyenlőség t=ak+m teljesül és egyenlőség t=ak+m ( m egész) esetén van ( m egész) esetén van
|
|
| [705] jenei.attila | 2012-03-13 09:14:30 |
 Szép feladat volt ez, és nagyon szép megoldásokat adtatok rá. Különösen az első tetszett, de Fálasz Mihályé is igen elegáns. A harmadik a vektorok használatának erejét mutatja, az is nagyon ügyes. Grat mindkettőtöknek.
|
| Előzmény: [702] HoA, 2012-03-09 10:49:57 |
|
| [704] HoA | 2012-03-09 14:43:39 |
 A szemléletes megoldások után jöjjön egy mechanikus, vektoralgebrai. Jelöljük a 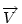 vektor 90 fokos pozitív elforgatottját vektor 90 fokos pozitív elforgatottját 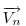 -nel, -nel, 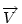 és és 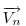 összegét összegét 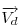 -vel . -vel . 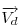 a a 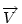 -vel 45 fokos szöget bezáró, -vel 45 fokos szöget bezáró,  hosszúságú vektor. Könnyen belátható, hogy tetszőleges hosszúságú vektor. Könnyen belátható, hogy tetszőleges 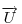 és és 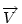 vektorokra vektorokra 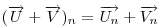
Legyen 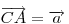 , , 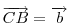 . Ekkor . Ekkor 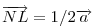 , , 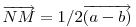 , , 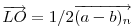 , , 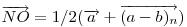 . Hasonlóan . Hasonlóan 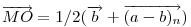
 . Mivel . Mivel  és és  adott hosszúságú vektorok, különbségük abszolút értéke akkor lesz a legnagyobb, ha egy egyenesbe esnek és ellentétes irányúak. adott hosszúságú vektorok, különbségük abszolút értéke akkor lesz a legnagyobb, ha egy egyenesbe esnek és ellentétes irányúak. 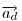 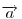 - hoz képest 45 fokra áll, tehát - hoz képest 45 fokra áll, tehát 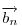 225 fokra és így 225 fokra és így 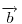 135 fokra. Hasonlóan adódik, hogy 135 fokra. Hasonlóan adódik, hogy 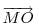 is akkor a leghosszabb, ha is akkor a leghosszabb, ha 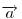 és és 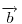 135 fokos szöget zár be. 135 fokos szöget zár be.
|
| Előzmény: [703] Fálesz Mihály, 2012-03-09 13:37:29 |
|





 =BIC
=BIC


 -egyenlőtlenség). Tehát
-egyenlőtlenség). Tehát  0-val, (2a+t)(2b+t)
0-val, (2a+t)(2b+t) fa,b(a+b). Behelyettesítve (*) adódik. Tehát
fa,b(a+b). Behelyettesítve (*) adódik. Tehát  -szerint periodikus, ezért az állítást elegendő abban az esetben bizonyítani, amikor
-szerint periodikus, ezért az állítást elegendő abban az esetben bizonyítani, amikor 