| [787] Róbert Gida | 2013-03-19 21:45:01 |
 "hogy ha g polinom fokszámánál több megoldása van" ez igaz, de itt mennyi is az f-f* fokszáma? Tipikusan legalább p, azaz nem is lehet neked több megoldásod.
|
| Előzmény: [783] w, 2013-03-18 20:37:00 |
|
|
| [785] w | 2013-03-19 15:07:21 |
 Az világos, egy korábbi hozzászólásomra utaltam, ami szerint igazoltam, hogy g fokszáma nem lehet p-nél kisebb. Nos, átgondoltam, és találtam benne elvi hibát. Azonban még áll az az ellentmondás, hogy g tetszőleges 0 konstans tagú lehet-e vagy g minden együtthatója p-vel osztható-e.
|
| Előzmény: [784] Fálesz Mihály, 2013-03-19 06:11:25 |
|
| [784] Fálesz Mihály | 2013-03-19 06:11:25 |
 A "megoldásokon" nem egész számokat, hanem mod p maradékosztályokat kell érteni.
Az f*(x)-f(x) 0 (mod p) kongruenciának csak p különböző mod p maradékosztály megoldása. 0 (mod p) kongruenciának csak p különböző mod p maradékosztály megoldása.
|
| Előzmény: [783] w, 2013-03-18 20:37:00 |
|
| [783] w | 2013-03-18 20:37:00 |
 Még mindig vannak az A582-vel kételyeim. Most szakirodalmat is találtam, ami azt állítja, hogy ha g polinom fokszámánál több megoldása van a g(x) 0 (mod p) kongruenciának, akkor annak minden együtthatója p-vel osztható. Ugyebár Kis-Fermat szerint p|f*-f. 0 (mod p) kongruenciának, akkor annak minden együtthatója p-vel osztható. Ugyebár Kis-Fermat szerint p|f*-f.
Ha találtok hibát, szóljatok.
|
|
| [782] w | 2013-03-15 21:55:06 |
 A. 582. Legyen p rögzített pozitív prímszám. Tetszőleges f(x) egész együtthatós polinomra legyen
f*(x)=f((1+x)p-1).
Határozzuk meg mindazokat a g egész együtthatós polinomokat, amelyekre teljesül a következő: minden pozitív egész n-hez van olyan f egész együtthatós polinom, amelyre a g-(f-f*) polinom n-nél kisebb fokú együtthatói mind oszthatók pn-nel.
Javasolta: Maga Péter (Budapest)
Megoldás. Először is látszik, hogy g-(f-f*) konstans tagja g konstans tagjával egyezik meg. Az egyetlen olyan egész szám, amely tetszőlegesen nagy számmal osztható, a nulla. Tehát g konstans tagja zérus.
Konstruálni fogunk minden ilyen polinomhoz egy-egy megfelelő f polinomot.
Vezessük be a cj(h) jelölést: ez a h polinom j fokú együtthatója lesz. A h-->h* képzés v-szer egymás utáni elvégeztekor kapott polinom legyen h(v) (v>0 egész).
Lemma. Legyen h egész együtthatós polinom úgy, hogy pm|cj(h), ha j=0,1,...,k-1, illetve pm-1|ck(h), de pm³ck(h) (m>0 egész). Ekkor pm|ci(h*) (i=0,1,2,...,k).
Bizonyítás. Az állítás i=0,1,2,...,k-1 esetén nyilvánvaló. Mivel a binomiális tétel szerint
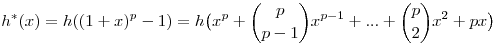 , ,
ezért a h* polinom képzelt alakjában ck(h*) a h polinom k-nál kisebb fokú együtthatóinak többszöröseiből tevődik össze, és még hozzáadódik p.ck(h) többszöröse. Így pm|ck(h*).
Alkalmazzuk a Lemmát h=g, k=1, m=1-re! Kapjuk, hogy p|c1(g(1)), mert c0(g)=c0(g(v))=0. Tegyük fel, hogy valamely k-ra p|cj(g(k-1)) minden j=0,1,2,…,k-1 esetén, ekkor a Lemma szerint p|ck(g(k)). A teljes indukció elveinek megfelelően kapjuk, hogy ez bármely k-ra igaz lesz, így például p|ci(g(n)) minden i=0,1,…,n –re.
Ezután alkalmazzuk a Lemmát h=g(n), k=1, m=2-re: p2|c1(g(n+1)). Az előzőhöz hasonlóan ismét folytathatunk k szerinti indukciót, amiből p2|cj(g(n+k)), ha j=0,1,…,k. Ennek eredményeként p2|ci(g(2n)) (i=0,1,…,n).
Tehát m szerinti teljes indukcióval, lépésenként k szerinti indukciót alkalmazva adódik, hogy
pn|ci(g(n2)) (i=0,1,…,n).
Válasszuk meg f polinomot úgy, hogy
f=g+g(1)+g(2)+…+g(n2-1).
Ekkor
f*=g(1)+g(2)+g(3)+…+g(n2), azaz
g-(f-f*)=g-(g-g(n2))=g(n2), és ez teljesíti a feltételeket.
Tehát pontosan azok a g polinomok felelnek meg, melyeknek konstans tagjuk nulla.
|
|
|
|
|
|
|
| [776] Maga Péter | 2013-03-15 10:30:56 |
 Tehát ha g konstans tagja 0, akkor g(l) n-nél kisebb fokú együtthatói pn-nel oszthatók. Legyen f=g(0)+g(1)+...+g(l-1). Mennyi ekkor g-(f-f*)?
|
| Előzmény: [775] w, 2013-03-15 10:14:24 |
|
| [775] w | 2013-03-15 10:14:24 |
 m=1, k=1: cf0,1(g*) 0 (mod p1) 0 (mod p1)
Tehát már m=2-re működik:
cf0,1(g(2)) 0 (mod p2). 0 (mod p2).
Indukcióval
cf0,1(g(k)) 0 (mod pk). 0 (mod pk).
(1)-ből kiindulva, m=2-re áttérve
cf0,1,2(g(2)) 0 (mod p1), 0 (mod p1),
így m, és "ezen belül" k szerinti indukcióval
cf0,1,...,m-1(g(m+k)) 0 (mod pk). 0 (mod pk).
Az látszik ebből, hogy a minimális  szám, melyre szám, melyre 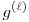 n-nél kisebb fokú együtthatói biztos pn-nel oszthatók, az n-nél kisebb fokú együtthatói biztos pn-nel oszthatók, az  =2n. =2n.
|
| Előzmény: [774] Maga Péter, 2013-03-15 00:23:33 |
|
| [774] Maga Péter | 2013-03-15 00:23:33 |
 Megpróbálom összefoglalni. Ha f olyan, hogy a konstans tagja 0, és benne a k-nál kisebb fokú együtthatók mind oszthatók pm-nel, és a pontosan k fokú együttható osztható pm-1-nel, akkor f*-ban a legfeljebb k fokú együtthatók mind oszthatók pm-nel.
Most azt bizonyítsd be, hogy ha g konstans tagja 0, akkor (rögzített n mellett) ha elég sokszor alkalmazzuk rá a *-ot, egy olyan polinomot kapunk, amelyben az n-nél kisebb fokú együtthatók pn-nel oszthatók. Tehát mondjuk legyen g(0)=g, g(1)=g*, általában g(k)=(g(k-1))*. Bizonyítsd be, hogy ha g konstans tagja 0, akkor elég nagy N-re (n előre rögzített), g(N) n-nél kisebb fokú együtthatói pn-nel oszthatók.
|
| Előzmény: [773] w, 2013-03-14 22:22:49 |
|
| [773] w | 2013-03-14 22:22:49 |
 Jelölje cfi(h) az h polinom i fokú együtthatóját.
Nyilván h=f* és i=1,2,3,...,k-1 esetén ez pm-mel osztható. Tekintsük cfk(f*)-t. A k-adfokú tagot a kisebb fokú tagok hozzák létre ( 0 mod pm), és még hozzáadódik az együtthatóhoz akp, ami ugyanezt teljesíti. cfk+1(f*) következik. Korábbi fokú tagok, ak is benne van, de ak+1p miatt semmit sem tudunk már erről (és nem is kell róla) mondani. 0 mod pm), és még hozzáadódik az együtthatóhoz akp, ami ugyanezt teljesíti. cfk+1(f*) következik. Korábbi fokú tagok, ak is benne van, de ak+1p miatt semmit sem tudunk már erről (és nem is kell róla) mondani.
Érdekes lépés. Végtelen leszállással próbáltam megközelíteni, de túlegyszerűsítettem a dolgot. Úgy látszik, itt is ez lesz.
Az f(x) polinom elég, ha n-edfokú (talán pár nulla "együtthatóval").
|
| Előzmény: [772] Maga Péter, 2013-03-14 16:08:17 |
|
| [772] Maga Péter | 2013-03-14 16:08:17 |
 Tegyük fel, hogy f(x)=aNxN+...+akxk+...+a1x, ahol a1,...,ak-1 mind oszthatók pm-nel, ak pedig nem osztható pm-nel, de osztható pm-1-gyel. Mit tudunk mondani f* kis fokú együtthatóiról a pm-nel való oszthatóságot illetően?
|
| Előzmény: [770] w, 2013-03-14 15:41:55 |
|
| [771] meowmeow | 2013-03-14 16:06:23 |
 B.4521-re első körben F1, F2, F3, M C egy körön vannak: ez trivi, kb szögszámolgatás, innét szerintem legegyszerűbb a C-re való inverzió, ekkor a két kis kör két párhuzamos egyenes lesz, a nagy kör meg ezeket érinti belülről, az érintő kör meg vele egyenlő sugarú lesz, és érinti ezeket. Innét minimális számolással (a C-n átmenő kör egyenes lesz) adódik az állítás.
|
|
|
| [769] w | 2013-03-14 15:41:18 |
 B.4520-hoz nem kell Titu-lemma, van könnyebb megoldás is. Legyen p:=(y+z)/2, q:=(z+x)/2, r:=(x+y)/2. Ha ezekkel számolunk, a közepek közötti becslések nem lesznek olyan élesek. Átírva a feladatbeli kifejezést:
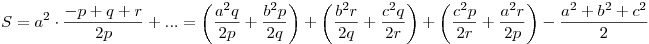
Ezt háromszor AM-GM-mel becsüljük, ekkor a, b, c háromszögoldalak mellett teljesül az összefüggés. (További vizsgálat a hivatalos megoldás szerint.)
|
|
| [768] w | 2013-03-14 15:25:38 |
 B.4515 megoldása.
Tekinthetjük a második dobást (1+2+3+4+5+6)/6=3,5-nek. Ugyanis a nyeremény várható értéke még egy dobás esetén ennek felel meg. Így elég csak az első dobással foglalkozni, illetve annak következményeivel. Feltehető még, hogy a játékos stratégikusan játszik.
Legyen az első dobás eredménye "a", a zseton ára "x". A játékos elméletileg választhat: 100a-x, vagy 350a-2x legyen a nyeresége. Akkor dob másodszor, ha 100a-x<350a-2x, azaz x/250<a.
Innen próbálgatással kapható, hogy 500<x<750. Tehát összességében a következő egyenletet elég megoldani:
100(1+2)-2x+350(3+4+5+6)-8x=0
6600=10x, x=660.
Ha a zseton ára 660 pénzegység, az üzemeltetőnek pont nulla a várható nyeresége. Tehát ennél nagyobb árú zsetonok kellenek.
-
Megjegyzés Róbert Gidának: a pénzegységet én választom meg :P (a játékot nyilván forintra találták ki) amúgy ha szigorúan vesszük igazad van :-) Azért nem így írtam a beküldött dolgozatban.
|
| Előzmény: [765] Róbert Gida, 2013-03-13 22:38:27 |
|
|
|
| [765] Róbert Gida | 2013-03-13 22:38:27 |
 Fent van már a megoldás. Bár attól elég távol van, arról sokat nem ír, hogy hogyan jött ki a megoldás. Javítóként ilyenre 0 pontot adtam volna másolás gyanúja miatt.
Egyébként az általános esetben is mindig van optimális tiszta stratégia, azaz olyan, hogy minden x-re px az nulla vagy egy. (Ezt könnyű látni).
Forintot meg ne írj, a feladat nem beszélt forintról, a megoldás sem.
|
| Előzmény: [763] w, 2013-03-13 17:06:41 |
|
| [764] w | 2013-03-13 19:28:01 |
 Jó nehéz volt a mostani A582. Van arra bizonyításom, hogy g fokszáma p-nél kisebb. Hogyan tovább? Van-e megoldásotok?
|
| Előzmény: [756] w, 2013-02-18 19:52:13 |
|
| [763] w | 2013-03-13 17:06:41 |
 Nem írtak ki a következő feladatra megoldást:
B.4515. Zseton bedobása után a játékautomata feldob egy szabályos játékkockát, majd megmutatja a dobás eredményét. Választhatunk: (1.) felvesszük a nyereményt - ami a dobott szám értékének 100-szorosa - és a játék véget ér, vagy (2.) újabb zsetont dobunk az automatába. Az utóbbi esetben a gép ismét dob, és a nyeremény a két dobott szám szorzatának a 100-szorosa. A játék legkésőbb a második dobás után véget ér. Legalább mennyi legyen a zseton ára, hogy az automata üzemeltetőjének hosszú távon nyeresége legyen?
____________________________________________________________________________________________________________
Tisztázásra vár, hogy mi a feladat helyes megoldása, hogy kell értelmezni a feltételeket. Nekem 660 jött ki, de érdekel a Ti megoldásotok is.
Igazoljuk, hogy ha a zseton ára 650 forint, a matematikus játékos számára nyereséges volna a játék.
Ezenkívül megkérdezném, mi volna, ha 1-től n-ig lehetnek a dobott számok, illetve ha más-más szorzót kap a dobott szám a kétféle körben. Mi van, ha három kör is van?
|
|





 0 (mod p) kongruenciának csak p különböző mod p maradékosztály megoldása.
0 (mod p) kongruenciának csak p különböző mod p maradékosztály megoldása. 
 szám, melyre
szám, melyre 