| [803] w | 2013-04-23 21:34:17 |
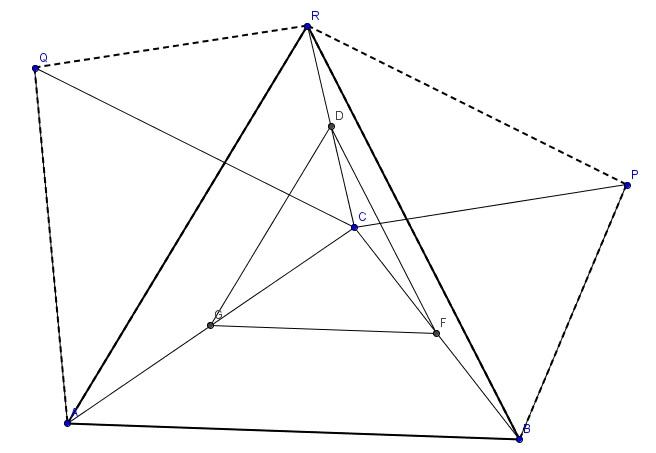
 B.4530 megoldása szebben.
Használva az ábra jelöléseit, nagyítsuk FGD-t C körül kétszeresére --> BAR háromszög. Itt CPRQ paralelogr., hisz kposan tükrös. Azt fogjuk igazolni, hogy ABR hasonló BCP-hez, egy további stratégiával: azt mutatjuk meg, hogy BR:BA=BP:BC és AR:AB=AQ:AC. Vegyük észre, hogy ABC, RBP és ARQ hasonló háromszögek! Pl. ABC és ARQ hasonló: AQR<=ACB< (szögszámítás) és AQ:QR=AQ:CP, ami AC:CB a hasonlóság miatt. Ugyanígy ABC hasonló RBP, tehát készen is vagyunk.
|
 |
|
| [802] w | 2013-04-23 17:42:34 |
 C. 1160. Mennyi a maradék, ha a 20122013+20132012 összeget elosztjuk 2012.2013-mal?
A hiv. megoldás binomiális tétellel készült. A versenykiírás szerint azonban "egy hónapon belül a kisebb sorszámú feladatokat ajánljuk a fiatalabb versenyzőknek". Ennek megfelelően az általános iskolás megoldás:
20132012=(2012+1)20132011=2012.20132011+20132011 20132011 (mod 2012.2013), 20132011 (mod 2012.2013),
és hasonló lépésekkel 20132012 20132011 20132011 ... ... 2013 (2012.2013), ugyancsak 2013 (2012.2013), ugyancsak
20122013=20122.20122011=(2011.2013+1).20122011 20122011 20122011 ... ... 2012 (mod 2012.2013). 2012 (mod 2012.2013).
Vagyis a maradék 2012+2013=4025.
|
|
|
|
| [799] m2mm | 2013-04-19 20:12:23 |
 Mondjuk olvasd el ennek a cikknek az alján levő három estere való írását:
http://www.komal.hu/cikkek/dandelin/dandelin.h.shtml
Utána mondjuk lásd be, hogy a kúp C csúcsának az ellipszis síkjára vett merőleges vetülete az AB nagytengelyen van, innen pedig azt lásd be, hogy CAB háromszög minden oldalát érinti a cikkben leírt beírt gömb. Innen B.4450. és adódik(persze itt nem csak az egyik hiperbolaíven lesznek pontok, mert a két fókuszpont bármelyikére bármelyik oldalra vehetjük a beírt gömböt), hogy a kérdéses pontok halmaza egy hiperbolán van, minek síkja merőleges az ellipszisére, és fókuszpontjai az ellipszis nagytengelyének végpontjai etc.
A többi kúpszeletre, ha érdekel nézd végig hasonlóan.
|
| Előzmény: [798] w, 2013-04-18 08:26:04 |
|
|
| [797] m2mm | 2013-04-18 01:03:39 |
 Ahogy én tapasztaltam A és B példák közti egyik fő különbség, hogy A-nál valami nagyobb, hatásosabb eszközt/módszert tudsz felfedezni magadtól/gyakorolni, míg a B-példák puzzle-ként kijönnek ált. max. 2 lépésben ha az ismert apró trükköket helyes sorrendben kihasználod.
Mostanában nincs időm nagyon A-kat nézegetni, B-k meg már nem mondanak újat, így
B.4525-öt sem oldottam meg, azaz nem tudom eldönteni A-ba való-e, ránézésre nem. Pláne mert a konstrukció(legalábbis a tied) nem igényel komolyabb hátteret, mint ld. pl. A.524.
Az általad említett A.542.-re én teljesen különböző megoldást találtam, de az is és a hiv. megoldás is azt mutatja hogy váratlanul "egyszerű" a megoldása általában egy komb. példának.
Nehézségre A.584. se valami nagy ügy, de Dandelin-gömb és B.4450 alap hozzá, B-be nem berakható. Mondjuk B.4450. előkerül A.570 megoldásánál is (bár vele csak az jön ki, hogy mi a megszerkesztendő pont valójában, onnan kell kicsi számolás a szerkesztéshez, de annak a feladatnak amúgy sem a szerkesztés kéne hogy legyen a lényege, csak a pont ily módon való meghatározása, de ez csak egyéni vélemény)
De a megoldáshoz nem kell ezeket tudni, arra is van az A-példa, hogy aki nem ismeri az magától rájöjjön ezekre. Mint ahogy pl. a Sawayama-lemmát se kell ismerned, az A-példák arra vannak hogy részeredményként belásd, aztán hiv. megoldásból tudod, hogy ezt így hívják.
|
| Előzmény: [796] w, 2013-04-17 19:33:06 |
|
|
| [795] w | 2013-04-14 19:59:20 |
 Senki? Fontos kiindulási adat, hogy az a1, a2, a3, a4 sorozat és az A1, A2, A3, A4 sorozat azonosan rendezett, enélkül talán nem is igaz az egyenlőtlenségem (?).
|
| Előzmény: [793] w, 2013-04-11 07:21:56 |
|
|
| [793] w | 2013-04-11 07:21:56 |
 A.588 (?) könnyítés:
Igazoljuk, hogy 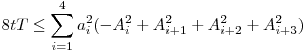 , ahol a két négyszög oldalai azonosan rendezettek. , ahol a két négyszög oldalai azonosan rendezettek.
|
|
| [792] w | 2013-04-11 07:18:20 |
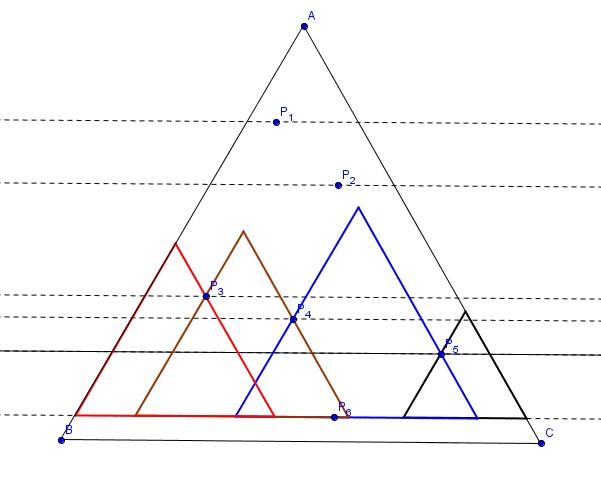
 De a mostani B.4525 is mehetett volna az A-ba. Nehéz konstrukciót találni. A következő pl. szerintem jó:
Rekurzív. Tfh. 2n-1 3-szög lefedi az (n-1) felvett belső pontú 3-szöget. Az n-edik Pn ponton át ||-t húztunk T oldalával (pn), a levágott 3-szög lefedhető (2n-1)-gyel. A maradó réteget úgy fedjük le, hogy meghosszabbítjuk a lefedők oldalait T oldaláig. A kapott háromszögek ha tartalmazzák Pn-et, húzzunk Pn-nel még két T-oldalirányban ||-t. A legnagyobb kétféle ilyet vegyük, mint új háromszög. Ez jó is lesz, mert lefedik a pn T-be eső részét a generálás módja miatt, és így a 3-szögek állásából lefedik az új "réteget".
Az ellenpélda n db pont egy T oldalával nem || egyenesen, ki-ki lássa be.
|
 |
| Előzmény: [791] w, 2013-04-08 16:32:23 |
|
| [791] w | 2013-04-08 16:32:23 |
 Egyetértek, ingadozó nehézségű A-jelű problémák vannak. Szerintem azt a feladatot azért tűzték ki, hogy kiszűrjék azokat, akik bemisztifikálják az A-feladatokat. Egyébként meg nem természetes, hogy most már négy olyan feladat is volt, melyre egyáltalán nem született megoldás. (Igaz, a mezőny sem olyan erős.) Sok olyan B-jelű 6 pontos feladatot látni, amely bőven méltó lenne az A-pontversenybe: B.4510, B.4511, B.4520, B.4521.
|
| Előzmény: [790] HoA, 2013-04-08 14:02:31 |
|
| [790] HoA | 2013-04-08 14:02:31 |
 Tudja valaki miért volt A.581 "A" feladat? Nekem a "Projektív geometria" téma [41] végén is leírt módon elég egyszerűnek tűnt.
|
|
| [789] Sinobi | 2013-04-08 12:06:58 |
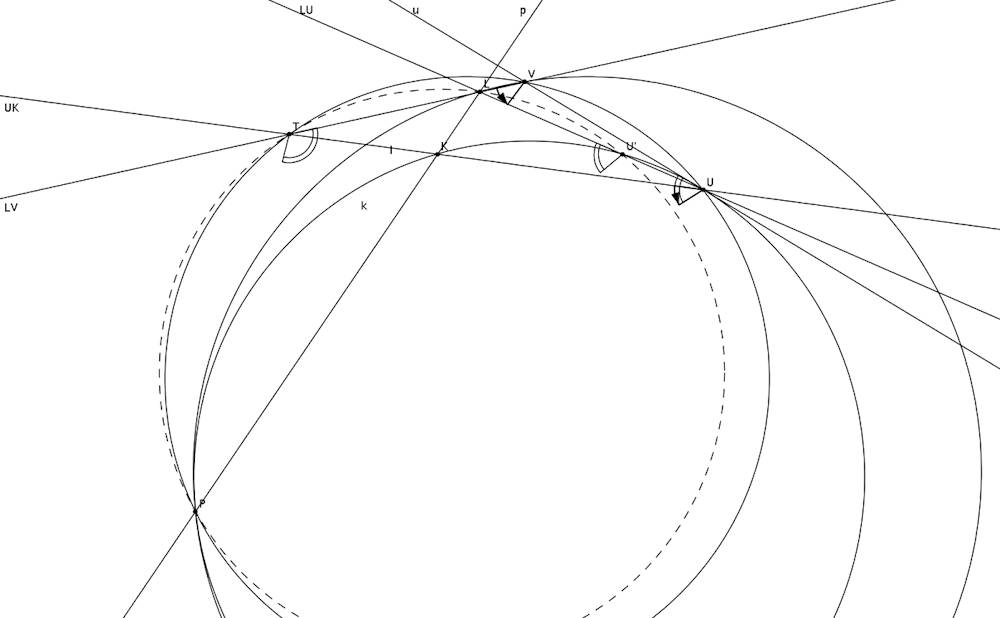
 A B4511-hez a hivatalosnál valamivel rövidebb megoldás:
Először azt látom be, hogy PUVT egy körön vannak: TP V-ből és U-ból is a KP szakasz k körre való irányított látószögéből látszik: PUT=PUK=PVL=PVT (lásd ábra, irányított nyilak)
Aztán azt látom be, hogy PU*LT is egy körön van (U* UL és K metszése): PL T-ből és U*-ból is PV szakasz PUVT körre való irányítot szögéből látszik: PTL=PTV=PUV=PU*U=PU*L (lásd ábra, dupla íves szögek)
L-ből egy olyan inverzió, ami k-t fixen hagyja UK-ból U*PL-t csinál, de UK-nak is része T, U*PL-nek is, tehát T csak UK és U*PL valamelyik metszéspontján lehet, ami meg eleme a merőleges körnek is.
|
 |
|
| [788] w | 2013-03-24 17:59:03 |
 A.569, A.571, A.573, A.574, A.580
Hasonlítsuk össze ezzel.
|
|
| [787] Róbert Gida | 2013-03-19 21:45:01 |
 "hogy ha g polinom fokszámánál több megoldása van" ez igaz, de itt mennyi is az f-f* fokszáma? Tipikusan legalább p, azaz nem is lehet neked több megoldásod.
|
| Előzmény: [783] w, 2013-03-18 20:37:00 |
|
|
| [785] w | 2013-03-19 15:07:21 |
 Az világos, egy korábbi hozzászólásomra utaltam, ami szerint igazoltam, hogy g fokszáma nem lehet p-nél kisebb. Nos, átgondoltam, és találtam benne elvi hibát. Azonban még áll az az ellentmondás, hogy g tetszőleges 0 konstans tagú lehet-e vagy g minden együtthatója p-vel osztható-e.
|
| Előzmény: [784] Fálesz Mihály, 2013-03-19 06:11:25 |
|
| [784] Fálesz Mihály | 2013-03-19 06:11:25 |
 A "megoldásokon" nem egész számokat, hanem mod p maradékosztályokat kell érteni.
Az f*(x)-f(x) 0 (mod p) kongruenciának csak p különböző mod p maradékosztály megoldása. 0 (mod p) kongruenciának csak p különböző mod p maradékosztály megoldása.
|
| Előzmény: [783] w, 2013-03-18 20:37:00 |
|
| [783] w | 2013-03-18 20:37:00 |
 Még mindig vannak az A582-vel kételyeim. Most szakirodalmat is találtam, ami azt állítja, hogy ha g polinom fokszámánál több megoldása van a g(x) 0 (mod p) kongruenciának, akkor annak minden együtthatója p-vel osztható. Ugyebár Kis-Fermat szerint p|f*-f. 0 (mod p) kongruenciának, akkor annak minden együtthatója p-vel osztható. Ugyebár Kis-Fermat szerint p|f*-f.
Ha találtok hibát, szóljatok.
|
|
| [782] w | 2013-03-15 21:55:06 |
 A. 582. Legyen p rögzített pozitív prímszám. Tetszőleges f(x) egész együtthatós polinomra legyen
f*(x)=f((1+x)p-1).
Határozzuk meg mindazokat a g egész együtthatós polinomokat, amelyekre teljesül a következő: minden pozitív egész n-hez van olyan f egész együtthatós polinom, amelyre a g-(f-f*) polinom n-nél kisebb fokú együtthatói mind oszthatók pn-nel.
Javasolta: Maga Péter (Budapest)
Megoldás. Először is látszik, hogy g-(f-f*) konstans tagja g konstans tagjával egyezik meg. Az egyetlen olyan egész szám, amely tetszőlegesen nagy számmal osztható, a nulla. Tehát g konstans tagja zérus.
Konstruálni fogunk minden ilyen polinomhoz egy-egy megfelelő f polinomot.
Vezessük be a cj(h) jelölést: ez a h polinom j fokú együtthatója lesz. A h-->h* képzés v-szer egymás utáni elvégeztekor kapott polinom legyen h(v) (v>0 egész).
Lemma. Legyen h egész együtthatós polinom úgy, hogy pm|cj(h), ha j=0,1,...,k-1, illetve pm-1|ck(h), de pm³ck(h) (m>0 egész). Ekkor pm|ci(h*) (i=0,1,2,...,k).
Bizonyítás. Az állítás i=0,1,2,...,k-1 esetén nyilvánvaló. Mivel a binomiális tétel szerint
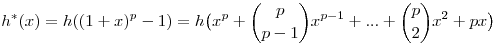 , ,
ezért a h* polinom képzelt alakjában ck(h*) a h polinom k-nál kisebb fokú együtthatóinak többszöröseiből tevődik össze, és még hozzáadódik p.ck(h) többszöröse. Így pm|ck(h*).
Alkalmazzuk a Lemmát h=g, k=1, m=1-re! Kapjuk, hogy p|c1(g(1)), mert c0(g)=c0(g(v))=0. Tegyük fel, hogy valamely k-ra p|cj(g(k-1)) minden j=0,1,2,…,k-1 esetén, ekkor a Lemma szerint p|ck(g(k)). A teljes indukció elveinek megfelelően kapjuk, hogy ez bármely k-ra igaz lesz, így például p|ci(g(n)) minden i=0,1,…,n –re.
Ezután alkalmazzuk a Lemmát h=g(n), k=1, m=2-re: p2|c1(g(n+1)). Az előzőhöz hasonlóan ismét folytathatunk k szerinti indukciót, amiből p2|cj(g(n+k)), ha j=0,1,…,k. Ennek eredményeként p2|ci(g(2n)) (i=0,1,…,n).
Tehát m szerinti teljes indukcióval, lépésenként k szerinti indukciót alkalmazva adódik, hogy
pn|ci(g(n2)) (i=0,1,…,n).
Válasszuk meg f polinomot úgy, hogy
f=g+g(1)+g(2)+…+g(n2-1).
Ekkor
f*=g(1)+g(2)+g(3)+…+g(n2), azaz
g-(f-f*)=g-(g-g(n2))=g(n2), és ez teljesíti a feltételeket.
Tehát pontosan azok a g polinomok felelnek meg, melyeknek konstans tagjuk nulla.
|
|
|
|
|




 20132011 (mod 2012.2013),
20132011 (mod 2012.2013), 






