|
|
| [840] Kardos | 2013-10-17 20:57:57 |
 B. 4559.-hez van valakinek valami ötlete?!?!? :) Előre is köszi!
|
|
| [839] n | 2013-10-13 17:49:17 |
 Azért az A595-höz a kétnégyzetszámos bizonyítás se' annyira ötlet, mert kb. rögtön kipotyog belőle a megoldás...
|
| Előzmény: [838] w, 2013-10-13 15:18:16 |
|
|
| [837] w | 2013-10-11 10:48:27 |
 Igen. (Pontosítás: k+1 pont határoz meg egy k fokszámú polinomot.)
Nyilván az volt a háttérbeli cél, hogy belássuk, hogyha érvényes a megadott feltétel, akkor a két polinom csak egymás eltoltja lehet. A következő kérdésem tehát az volna, hogyha deg(P)=deg(Q)=n, a feltétel marad, és P(x) Q(x+k) (k>0), akkor mekkora lehet k? Q(x+k) (k>0), akkor mekkora lehet k?
|
| Előzmény: [836] Sinobi, 2013-10-11 10:41:18 |
|
| [836] Sinobi | 2013-10-11 10:41:18 |
 Nem léteznek. Egy idő után mind a kettő monoton lesz (legyen monoton növő), és nagyobb az addigi felvett értékeknél.
Ebből következik, hogy egy idő után ha p(x)=q(z), akkor p(x+n)=q(z+n), minden természetes n-re. Legyen p és q közül a nagyobb fokszma k. Mivel k pontra egyértelműen illeszthető k (vagy annál kisebb, ha létezik) fokszámú polinom, véve az (x,p(x)), (x+1,p(x+1)),...(x+k,p(x+k)) és (z,q(z)), (z+1,q(z+1)),...(z+k,q(z+k)) pontokat, ezek egyértelműen meghatározzák p-t, és q-t is, és ezek a pontok egymásba eltolhatóak, tehát p és q is egymásba eltolható, tehát ugyanannyi a fokszámuk, ha léteznek.
|
| Előzmény: [835] w, 2013-10-11 10:25:59 |
|
| [835] w | 2013-10-11 10:25:59 |
 B.4561-hez egy nehéz, de nagyon érdekes csatlakozó kérdés:
Léteznek-e olyan különböző fokszámú P és Q polinomok, melyeknek természetes számokon vett értékkészleteik megegyeznek?
|
|
| [834] w | 2013-07-07 08:32:26 |
 Melyik a könnyebb: B.4149 vagy B.4536? Érdekes, hogy az ilyen ismétlődő feladatokat akkor találjuk meg, mikor legkevésbé keressük őket :-) A megfogalmazást, a hiv. megoldás hosszát és a statisztikát is érdemes megfigyelni.
|
|
|
| [832] rizsesz | 2013-06-28 14:51:26 |
 A C.1168-ba olyan szepen bele lehet irni a=sinx-et es b=siny-t. Elnezest, konnyed, valoszinuleg mindenki szamara trivialis gondolat :-)
|
|
| [831] w | 2013-06-21 19:32:38 |
 B.4540 általánosabban. Adott n db matematikus rab egy börtönben. Játék: s-féle színű sapkák vannak, minden rab kap egyet a fejére. Mindenki csak a többiek sapkáját látja. Egyszerre tippelnek saját sapkájuk színére. Határozzuk meg azt a maximális k(n,s) számot, melyre alkalmas stratégiával ennyi jó tipp mindig születhet.
|
|
| [830] w | 2013-06-20 17:58:23 |
 "Ha jól látom, azt nem láttad be, hogy k1 érinti k-t." - "őizé"
Bocs, nem voltam elég figyelmes, körsor, azaz "1" nálam kiesett. Így viszont már eléggé tetszik az összehozott megoldás.
|
| Előzmény: [829] Sinobi, 2013-06-20 17:17:42 |
|
| [829] Sinobi | 2013-06-20 17:17:42 |
 őizé.
igen, azt hiszem ez egy egyszerűbb megoldás, hogy
1: a három kör egyszerre és egy pontban érinti egymást, mert.
2: k1 és k érintik egymást, mert Sawayama-lemma
|
| Előzmény: [828] w, 2013-06-20 10:29:28 |
|
| [828] w | 2013-06-20 10:29:28 |
 "Minden illeszkedés feladat kitrigonometriázható. Ahogy kijön koordinátákkal, vektorokkal, komplex számokkal, k darab Pascal/Desargues tétel felírásával, etc."
Bocs, én úgy értettem, hogy a feladat csak trigonometriával két oldalon belül is megoldható, és egészen triviális úton. Az más kérdés, hogy te többet láttál be, a hiv. megoldás még többet, de itt szerintem a trigonometriával való megközelítés egészen természetes volt ("elég szabályos az ábra" stb.). Ismerek olyan megoldót is, aki hamar feladja a geometriai okoskodást, és 10-20 oldalas koordinátás megoldásokat küld be ehelyett! (Az igazat megvallva lusta voltam szépen megoldani :-).)
"...tehát k-t is érinti, tehát k1-et is, kész."
Ha jól látom, azt nem láttad be, hogy k1 érinti k-t. Van rá egy egyszerű bizonyítás az A.579-ből már jól ismert Sawayama-lemmával. ;-)
A megoldásod egyébként eléggé tetszik, mutatja az inverzió erejét.
|
| Előzmény: [826] Sinobi, 2013-06-19 15:09:05 |
|
| [827] Sinobi | 2013-06-19 15:41:08 |
 szerk: na jó, hátha hasznos (+ valaki aki ért hozzá majd kijavít)
Tetszőleges P-re k, k1, k2 egy körsoron van, mert
Berajzoltam az egyenlő szögeket, amikből látszik, hogy
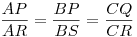
Tudjuk, hogy az érintő hossznégyzete a pont körre vonatozó hatványával egyezik meg, ami meg ha pontot helyettesítünk a kör egyenletébe:
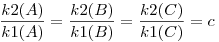
Felszorozva azt kapjuk, hogy a k kör A, B, C pontjára: k2(A)-ck1(A)=0=k(A), azaz k előáll a másik két kör egyenletének lineáris kombinációjaként (három pontban), k egy körsoron van velük.
|
 |
| Előzmény: [826] Sinobi, 2013-06-19 15:09:05 |
|
| [826] Sinobi | 2013-06-19 15:09:05 |
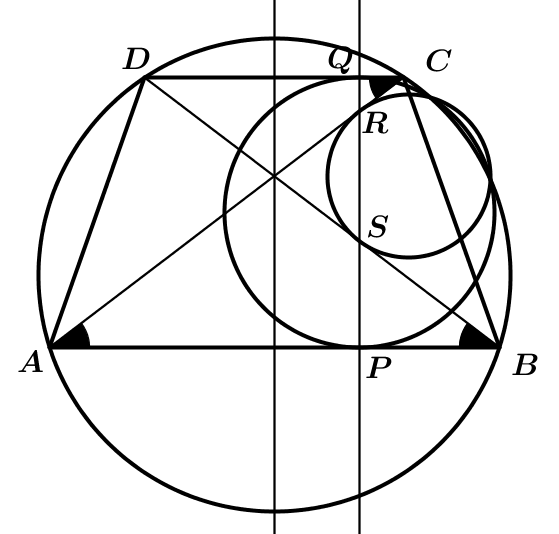
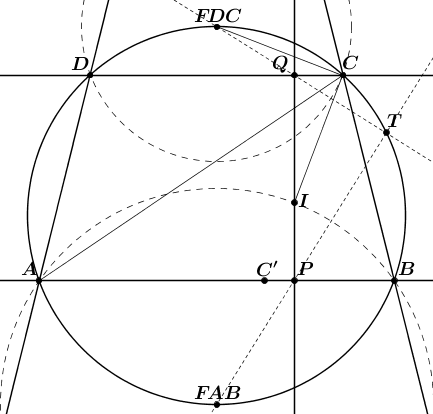
 ,,Könnyű észrevenni, hogy nincs szükségünk semmilyen új körre, hisz elég szabályos az ábra, ott vannak a párhuzamosok és merőlegesek. Átírhatjuk egy trigonometriapéldára a feladatot. "
Minden illeszkedés feladat kitrigonometriázható. Ahogy kijön koordinátákkal, vektorokkal, komplex számokkal, k darab Pascal/Desargues tétel felírásával, etc.
Az enyém valamivel elemibb geometriát használ, csak sokat:
1. Először belátom, hogy k1, k2 és k egy körsoron vannak. Ezt most nem bizonyítom. Utána azt fogom belátni, hogy k2 és k (a trapéz körülírt köre) érintik egymást.
2. A Thalész-tétel értelmében ha a FAB-P és a FDC-Q egyenesek a k körön metszik egymást, akkor a PQ Thalész-köre is átmegy azon a ponton. (FAB az AB ív felezőpontja, FDC hasonlóan). Legyen FAB-P metszése k körrel T, azt akarom belátni, hogy FDC, Q és T egy egyenesen van.
3. Az ABC háromszög I beírt körének középpontja rajta a FAB kp-jú, A-n átmenő körön (ez ismert). IC Thalészkörén rajta van Q, és rajta van T is, mert egy FAB kp-jú inverzió után T képe P rajta van IC' Thalész-körén.
4. Mivel az FDC-C szakasz érinti az ITCQ kört, FDC-re vonnatkozó inverzió után a kör helyben marad, Q és T kicserélődik, tehát FDC, Q és T egy egyenesen van.
5. FAB-ra vonatkozó inverzió esetén PQT átmegy egy ponton és a képén, P-n és T-n, tehát fixkör. Az AB oldalt érintette, tehát k-t is érinti, tehát k1-et is, kész.
|
 |
| Előzmény: [825] w, 2013-06-19 12:36:28 |
|
| [825] w | 2013-06-19 12:36:28 |
 B.4551. A hiv. megoldás nem valami egyszerű, maga a feladat sokkal könnyebb. Könnyű észrevenni, hogy nincs szükségünk semmilyen új körre, hisz elég szabályos az ábra, ott vannak a párhuzamosok és merőlegesek. Átírhatjuk egy trigonometriapéldára a feladatot.
A ki kör középpontja Oi, sugara ri (i=1,2); AC BD=M; BD=M; 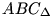 -ben a szokásos jelölések érvényesek. Elég megmutatni, hogy a két kör belülről érinti egymást, azaz O1O2=|r1-r2|. -ben a szokásos jelölések érvényesek. Elég megmutatni, hogy a két kör belülről érinti egymást, azaz O1O2=|r1-r2|.
Először is AP=AC-BC+BP=AC-BC+(AB-AP)  AP=(b+c-a)/2. AP=(b+c-a)/2.
Világos, hogy 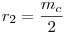 . .
Legyen M vetülete AB-re Mx, PQ-ra My. Ekkor AMx=c/2, majd MxP=AP-AMx=(b-a)/2. Nyilván My MO1, ahonnan MO1, ahonnan
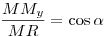 és és  , ,
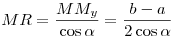 , ,
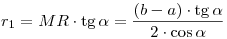 . .
Továbbá
MMx=AMx.tg  =c.tg =c.tg  /2, ezért /2, ezért
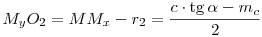 ; ;
MyO1=r1.sin  , ,
és így
O1O22=MyO12+MyO22.
Ekvivalens átalakításokkal
O1O2=|r1-r2|
O1O22=(r1-r2)2
MyO12+MyO22=r12+r22-2r1r2
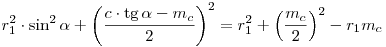

c2tg2 -2cmctg -2cmctg  +mc2=4r12cos2 +mc2=4r12cos2 +mc2-4r1mc +mc2-4r1mc


c2-2bccos  =(b-a)2-2b(b-a) =(b-a)2-2b(b-a)
c2-2bccos  =b2-2ab+a2-2b2+2ab =b2-2ab+a2-2b2+2ab
b2+c2-2bccos  =a2 =a2
Azonosság.
|
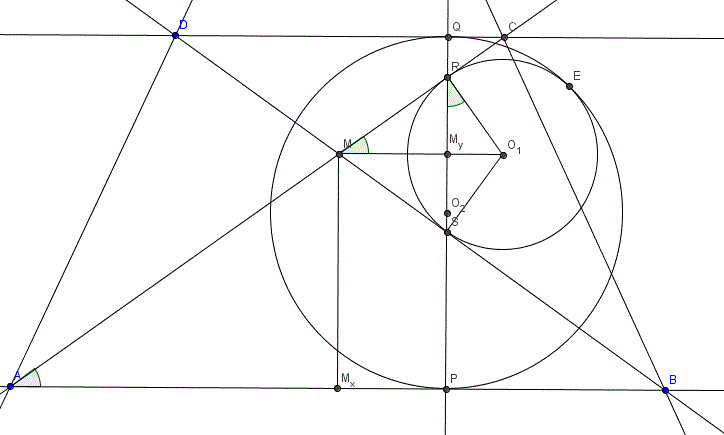 |
|
|
| [823] w | 2013-06-11 21:18:22 |
 A vége kicsit hibádzott, mert a=2-re és 3-ra is található megfelelő polinom:
p2(x)=-2x2+3x+8, ahol
p2(22/3+21/3)=-2(2.21/3+22/3+4)+3(22/3+21/3)+8=-4.21/3-2.22/3-8+3.22/3+3.21/3+8=22/3-21/3, és
p3(x)=-x2+2x+6, ahol
p3(32/3+31/3)=-3.31/3-6-32/3+2.32/3+2.31/3+6=32/3-31/3.
Az én megoldásom (elvben kicsit egyszerűbb) a következő lépésekből áll (biz. be!).
1. Kizárjuk a köbszámokat, rögzítjük a-t.
2. Az 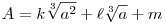 kifejezés irracionális szám, ahol k és kifejezés irracionális szám, ahol k és  nem egyszerre nulla (illetve k, nem egyszerre nulla (illetve k, ,m ,m Z). Z).
(Ez lényegében a te első lemmád.)
3. Következmény: A 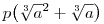 kifejezés egyértelműen előáll kifejezés egyértelműen előáll 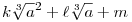 alakban (a 3. lemmád) alakban (a 3. lemmád)
4. (Ez a legfontosabb meglátás:) Legyen rögzített a és p mellett

alakú. Ekkor k  (mod (a-1)). (mod (a-1)).
(Biz.: a konstans és elsőfokú polinomokra kész vagyunk, és két ilyen polinom összege vagy szorzata is ilyen.)
5. Következmény: Világos, hogyha p(a2/3+a1/3)=a2/3-a1/3, akkor 1 -1 (mod (a-1)), tehát a-1|1-(-1)=2, és így csakis a=3,2,0,-1 lehet (kizártuk a köbszámok esetét) --> a=2,3. -1 (mod (a-1)), tehát a-1|1-(-1)=2, és így csakis a=3,2,0,-1 lehet (kizártuk a köbszámok esetét) --> a=2,3.
Pontosan azokhoz az a számokhoz létezik megfelelő p polinom, melyek egész számok köbei, vagy a=2,3.
|
| Előzmény: [822] aaaa, 2013-06-11 17:59:29 |
|
| [822] aaaa | 2013-06-11 17:59:29 |
 A.590.
Lemma 1.
 lineárisan függetlenek Q felett, ha t racionális és nem egy racionális szám köbe. Ekkor ugyanis ez a 3 érték páronként lineárisan független, ez triviális. Tegyük fel, hogy függő rendszert alkotnak, ekkor megfelelő racionális számokra: lineárisan függetlenek Q felett, ha t racionális és nem egy racionális szám köbe. Ekkor ugyanis ez a 3 érték páronként lineárisan független, ez triviális. Tegyük fel, hogy függő rendszert alkotnak, ekkor megfelelő racionális számokra:  + + t1/3=t2/3. Ezt köbre emelve, majd az előbbi összefüggést behelyettesítve a következő adódik: t1/3=t2/3. Ezt köbre emelve, majd az előbbi összefüggést behelyettesítve a következő adódik:

Ez 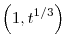 Q feletti lineáris függetlensége miatt csak akkor lehetséges, ha Q feletti lineáris függetlensége miatt csak akkor lehetséges, ha
 3+3 3+3 2 2 2+ 2+ 3t-t2=0 3t-t2=0
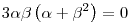
Ebből a  =0, =0,  =0 és =0 és  =- =- 2 esetek adódnak, aminek a megoldása t-re rendre: 2 esetek adódnak, aminek a megoldása t-re rendre:  , , 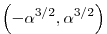 és és 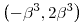 . Ezek közül t=2 . Ezek közül t=2 3 nem ad megoldást, mert visszavezet a - 3 nem ad megoldást, mert visszavezet a - 2+ 2+ 221/3= 221/3= 222/3 egyenlőségre, ami nyilvánvalóan hamis, a többi esetben t köbszám lesz, ha racionális, de feltettük, hogy ez nem igaz. Ezzel beláttuk, hogy függetlenek. 222/3 egyenlőségre, ami nyilvánvalóan hamis, a többi esetben t köbszám lesz, ha racionális, de feltettük, hogy ez nem igaz. Ezzel beláttuk, hogy függetlenek.
Lemma 2.
 := := + + t1/3+ t1/3+ t2/3 gyöke a következő t2/3 gyöke a következő ![p \left( x \right) \in {Q} \left[ x \right]](keplet.cgi?k=861402527471855C) polinomnak, ahol polinomnak, ahol  , , , , ,t racionális számok: ,t racionális számok:

Ezt egy egyszerű behelyettesítéssel ellenőrizhetjük.
Lemma 3.
Ha valamely ![f \left( x \right) \in {Q} \left[ x \right]](keplet.cgi?k=97995E51AE9E752C) polinomra polinomra 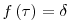 , akkor , akkor ![\exists r \left( x \right)
\in {Q} \left[ x \right]](keplet.cgi?k=E1B9E2B615591ECE) , ahol , ahol  foka legfeljebb 2 és foka legfeljebb 2 és  . Legyen ugyanis . Legyen ugyanis 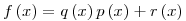 alakú, ahol alakú, ahol 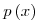 az előbbi polinom, és itt egy maradékos osztást végeztünk, így az előbbi polinom, és itt egy maradékos osztást végeztünk, így  foka maximum 2. Ekkor, kihasználva foka maximum 2. Ekkor, kihasználva 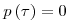 -t: -t: 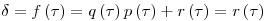
A feladat állításának bizonyítása:
Ha a=t3 köbszám, akkor mivel egész, a  konstans függvény jó. Egyébként pedig: a2/3+a1/3 gyöke Lemma 2. miatt konstans függvény jó. Egyébként pedig: a2/3+a1/3 gyöke Lemma 2. miatt 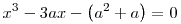 -nak. Lemma 3. miatt elég tehát ellenőrizni, hogy állhat-e -nak. Lemma 3. miatt elég tehát ellenőrizni, hogy állhat-e  , , , , racionálisakkal: racionálisakkal:
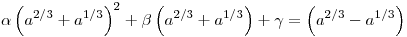
Vagyis:
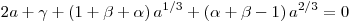
Mivel 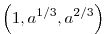 lineárisan függetlenek, ezért mindhárom együttható 0 kellene, hogy legyen, de ez nem lehetséges, mert -1= lineárisan függetlenek, ezért mindhárom együttható 0 kellene, hogy legyen, de ez nem lehetséges, mert -1= + + =1 kellene, ezért nincs ilyen polinom. =1 kellene, ezért nincs ilyen polinom.
|
|
| [821] w | 2013-06-11 06:57:16 |
 Két kérdés. Hogyan lehet-e egyáltalán nekikezdeni az A.592 feladatnak? Még a triviális esetek is iszonyatosak. Ezenkívül mi okból lett az A.591 "A-jelű" feladat, egyszerű érintőszakaszos megoldása van, itt még általánosítás is található.
|
|
|
| [819] nadorp | 2013-05-16 10:37:38 |
 Kedves Mihály,
Köszönöm a kiegészítést, erre nem gondoltam. A poén az, hogy amikor először "nekiestem" a feladatnak, akkor én is próbálkoztam ezzel a körosztási polinommal, de nem jutottam dűlőre, egészen másfelé kalandoztam el.
|
| Előzmény: [1087] Fálesz Mihály, 2013-05-16 10:05:01 |
|
| [1087] Fálesz Mihály | 2013-05-16 10:05:01 |
 Szia Péter,
Köszi, hogy leírtad.
Szerintem azért legbelül a két megoldás lényege ugyanaz: találunk egy hetedrendő elemet (ha tetszik, hetedik egységgyököt) \(\displaystyle GF_{p^2}\)-ben.
Ha a Kearnes-Kiss-Szendrei cikket követjük, akkor az \(\displaystyle \Phi_7(x)=1+x+x^2+x^3+x^4+x^5+x^6\) körosztási polinom egyik gyökét keressük. Ha \(\displaystyle p\ne7\), akkor \(\displaystyle \Phi_7(1)\ne0\), így a \(\displaystyle \Phi_7\) gyökei tényleg hetedrendűek.
Mivel \(\displaystyle \Phi_7\) páros fokú palindrom polinom, a szokásos módon eloszthatjuk \(\displaystyle x^3\)-bel, és átírhatjuk \(\displaystyle x+\frac1x\) polinomjává:
\(\displaystyle
\frac{\Phi_7(x)}{x^3} = x^3+x^2+x+1+\frac1x+\frac1{x^2}+\frac1{x^3} = \left(x+\frac1x\right)^3+\left(x+\frac1x\right)^2-2\left(x+\frac1x\right)-1 =
\Psi_7\left(x+\frac1x\right).
\)
Ha \(\displaystyle \Psi_7\)-nek van egy \(\displaystyle u\) gyöke \(\displaystyle GF_p\)-ben, akkor \(\displaystyle \Phi_7\)-nek is van (0-tól különböző) gyöke \(\displaystyle GF_{p^2}\)-ben: az \(\displaystyle x^2-ux+1\) polinom gyökei ilyenek.
Ha pedig van hetedrendű elem, akkor a multiplikatív csoport rendje, \(\displaystyle p^2-1\) osztható az elem rendjével, \(\displaystyle 7\)-tel.
* * *
A feladatban szereplő polinom a \(\displaystyle \Psi_7\) egy transzformáltja:
\(\displaystyle
7x(x+1)^2-1 = (x+1)^3 \Psi_7\left(2-\frac1{x+1}\right).
\)
Ha \(\displaystyle 7a(a+1)^2-1\equiv 0~(\mod~p)\), akkor \(\displaystyle p\ne7\), \(\displaystyle GF_p\)-ben \(\displaystyle a\ne-1\), és \(\displaystyle 2-\frac1{a+1}\) gyöke \(\displaystyle \Psi_7\)-nek.
* * *
Mindkét megoldásban úgy kerestük a hetedik egységgyököket, hogy először felírtunk egy harmadfokú polinomot, aminek valamilyen szorosabb köze van a \(\displaystyle \cos\frac{2k\pi}7\) számokhoz (a Te esetedben \(\displaystyle c=\tg^2\frac{k\pi}7=\frac{1-\cos\frac{2k\pi}7}{1+\cos\frac{2k\pi}7}\)), ennek volt egy modulo \(\displaystyle p\) gyöke, és ebből egy másodfokú egyenlet adott egy hetedik egységgyököt \(\displaystyle GF_{p^2}\)-ben.
|
| Előzmény: [816] nadorp, 2013-05-15 21:21:29 |
|






 Q(x+k) (k>0), akkor mekkora lehet k?
Q(x+k) (k>0), akkor mekkora lehet k? x,y
x,y


 BD=M;
BD=M;  AP=(b+c-a)/2.
AP=(b+c-a)/2.  MO1, ahonnan
MO1, ahonnan  =c.tg
=c.tg 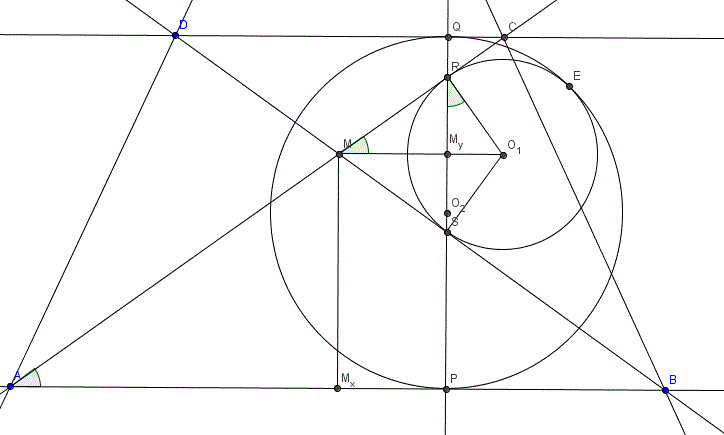
 ,
, egészek:
egészek:  nem egyszerre nulla (illetve k,
nem egyszerre nulla (illetve k, :=
:=