|
| [846] w | 2013-10-29 19:44:42 |
 Tehát az én megoldásom (vázlatos):
Vegyük észre, hogy
a) a1+a2+...+a2013=2014
b) a1+2a2+...+2013a2013=4026.
Emellett vezessük be ak-t, mint a legutolsó olyan ai szám a mondatban, ami még nem nulla. Mivel minden szám legfeljebb k-szor fordul elő a mondatban, és a nullák száma legalább 2013-k, így k 2013-k, k>1006. De ez azt jelenti, hogy ak=1, és k darab nulla van a mondatban. Tehát ai sorozatban 2013-k darab nem nulla szám van, ezek közül kettő a1 és ak. 2013-k, k>1006. De ez azt jelenti, hogy ak=1, és k darab nulla van a mondatban. Tehát ai sorozatban 2013-k darab nem nulla szám van, ezek közül kettő a1 és ak.
Vonjuk ki a)-t b)-ből, amit kapunk, azt pedig becsüljük meg alulról:
![2012=\sum_{i=2}^k (i-1)a_i=\sum_{i=2}^{k-1}(i-1)a_i+ka_k\ge[1+2+\dots+(2011-k)]+k=[1+2+\dots+(2010-k)]+2011](keplet.cgi?k=FCA691FC5F319BCB)
Ebből adódik, hogy k>2008 is igaz. Innen kis gondolkodás és kész.
|
| Előzmény: [844] w, 2013-10-21 21:05:42 |
|
| [845] Róbert Gida | 2013-10-23 21:22:38 |
 Aki a feltett megoldásokat elolvassa nagy előnyben van: http://www.komal.hu/verseny/feladat.cgi?a=feladat&f=A588&l=hu
http://www.komal.hu/verseny/feladat.cgi?a=feladat&f=A595&l=hu
|
|
| [844] w | 2013-10-21 21:05:42 |
 Talán a legnehezebb szeptemberi B-feladat (legalábbis számomra) a B.4552-es volt:
Ebben a mondatban az 1 alkalommal előforduló számok száma a1,
a 2 alkalommal előforduló számok száma a2,
...,
a 2013 alkalommal előforduló számok száma a2013.
Adjuk meg az a1,a2,...,a2013 számokat úgy, hogy igaz állítást kapjunk. Hányféleképpen tehetjük ezt meg?
Hogyan oldottátok meg? (Nekem van egy relatívan szép és egyszerű megoldásom, de kíváncsi vagyok, hogy Ti mit kezdettetek vele. Az eredeti javasolt megoldás is érdekelne.)
|
|
|
|
|
| [840] Kardos | 2013-10-17 20:57:57 |
 B. 4559.-hez van valakinek valami ötlete?!?!? :) Előre is köszi!
|
|
| [839] n | 2013-10-13 17:49:17 |
 Azért az A595-höz a kétnégyzetszámos bizonyítás se' annyira ötlet, mert kb. rögtön kipotyog belőle a megoldás...
|
| Előzmény: [838] w, 2013-10-13 15:18:16 |
|
|
| [837] w | 2013-10-11 10:48:27 |
 Igen. (Pontosítás: k+1 pont határoz meg egy k fokszámú polinomot.)
Nyilván az volt a háttérbeli cél, hogy belássuk, hogyha érvényes a megadott feltétel, akkor a két polinom csak egymás eltoltja lehet. A következő kérdésem tehát az volna, hogyha deg(P)=deg(Q)=n, a feltétel marad, és P(x) Q(x+k) (k>0), akkor mekkora lehet k? Q(x+k) (k>0), akkor mekkora lehet k?
|
| Előzmény: [836] Sinobi, 2013-10-11 10:41:18 |
|
| [836] Sinobi | 2013-10-11 10:41:18 |
 Nem léteznek. Egy idő után mind a kettő monoton lesz (legyen monoton növő), és nagyobb az addigi felvett értékeknél.
Ebből következik, hogy egy idő után ha p(x)=q(z), akkor p(x+n)=q(z+n), minden természetes n-re. Legyen p és q közül a nagyobb fokszma k. Mivel k pontra egyértelműen illeszthető k (vagy annál kisebb, ha létezik) fokszámú polinom, véve az (x,p(x)), (x+1,p(x+1)),...(x+k,p(x+k)) és (z,q(z)), (z+1,q(z+1)),...(z+k,q(z+k)) pontokat, ezek egyértelműen meghatározzák p-t, és q-t is, és ezek a pontok egymásba eltolhatóak, tehát p és q is egymásba eltolható, tehát ugyanannyi a fokszámuk, ha léteznek.
|
| Előzmény: [835] w, 2013-10-11 10:25:59 |
|
| [835] w | 2013-10-11 10:25:59 |
 B.4561-hez egy nehéz, de nagyon érdekes csatlakozó kérdés:
Léteznek-e olyan különböző fokszámú P és Q polinomok, melyeknek természetes számokon vett értékkészleteik megegyeznek?
|
|
| [834] w | 2013-07-07 08:32:26 |
 Melyik a könnyebb: B.4149 vagy B.4536? Érdekes, hogy az ilyen ismétlődő feladatokat akkor találjuk meg, mikor legkevésbé keressük őket :-) A megfogalmazást, a hiv. megoldás hosszát és a statisztikát is érdemes megfigyelni.
|
|
|
| [832] rizsesz | 2013-06-28 14:51:26 |
 A C.1168-ba olyan szepen bele lehet irni a=sinx-et es b=siny-t. Elnezest, konnyed, valoszinuleg mindenki szamara trivialis gondolat :-)
|
|
| [831] w | 2013-06-21 19:32:38 |
 B.4540 általánosabban. Adott n db matematikus rab egy börtönben. Játék: s-féle színű sapkák vannak, minden rab kap egyet a fejére. Mindenki csak a többiek sapkáját látja. Egyszerre tippelnek saját sapkájuk színére. Határozzuk meg azt a maximális k(n,s) számot, melyre alkalmas stratégiával ennyi jó tipp mindig születhet.
|
|
| [830] w | 2013-06-20 17:58:23 |
 "Ha jól látom, azt nem láttad be, hogy k1 érinti k-t." - "őizé"
Bocs, nem voltam elég figyelmes, körsor, azaz "1" nálam kiesett. Így viszont már eléggé tetszik az összehozott megoldás.
|
| Előzmény: [829] Sinobi, 2013-06-20 17:17:42 |
|
| [829] Sinobi | 2013-06-20 17:17:42 |
 őizé.
igen, azt hiszem ez egy egyszerűbb megoldás, hogy
1: a három kör egyszerre és egy pontban érinti egymást, mert.
2: k1 és k érintik egymást, mert Sawayama-lemma
|
| Előzmény: [828] w, 2013-06-20 10:29:28 |
|
| [828] w | 2013-06-20 10:29:28 |
 "Minden illeszkedés feladat kitrigonometriázható. Ahogy kijön koordinátákkal, vektorokkal, komplex számokkal, k darab Pascal/Desargues tétel felírásával, etc."
Bocs, én úgy értettem, hogy a feladat csak trigonometriával két oldalon belül is megoldható, és egészen triviális úton. Az más kérdés, hogy te többet láttál be, a hiv. megoldás még többet, de itt szerintem a trigonometriával való megközelítés egészen természetes volt ("elég szabályos az ábra" stb.). Ismerek olyan megoldót is, aki hamar feladja a geometriai okoskodást, és 10-20 oldalas koordinátás megoldásokat küld be ehelyett! (Az igazat megvallva lusta voltam szépen megoldani :-).)
"...tehát k-t is érinti, tehát k1-et is, kész."
Ha jól látom, azt nem láttad be, hogy k1 érinti k-t. Van rá egy egyszerű bizonyítás az A.579-ből már jól ismert Sawayama-lemmával. ;-)
A megoldásod egyébként eléggé tetszik, mutatja az inverzió erejét.
|
| Előzmény: [826] Sinobi, 2013-06-19 15:09:05 |
|
| [827] Sinobi | 2013-06-19 15:41:08 |
 szerk: na jó, hátha hasznos (+ valaki aki ért hozzá majd kijavít)
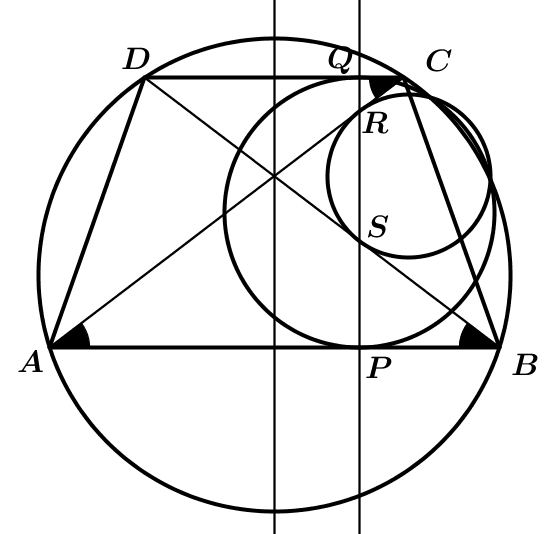
Tetszőleges P-re k, k1, k2 egy körsoron van, mert
Berajzoltam az egyenlő szögeket, amikből látszik, hogy
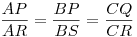
Tudjuk, hogy az érintő hossznégyzete a pont körre vonatozó hatványával egyezik meg, ami meg ha pontot helyettesítünk a kör egyenletébe:
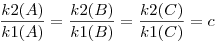
Felszorozva azt kapjuk, hogy a k kör A, B, C pontjára: k2(A)-ck1(A)=0=k(A), azaz k előáll a másik két kör egyenletének lineáris kombinációjaként (három pontban), k egy körsoron van velük.
|
 |
| Előzmény: [826] Sinobi, 2013-06-19 15:09:05 |
|
| [826] Sinobi | 2013-06-19 15:09:05 |
 ,,Könnyű észrevenni, hogy nincs szükségünk semmilyen új körre, hisz elég szabályos az ábra, ott vannak a párhuzamosok és merőlegesek. Átírhatjuk egy trigonometriapéldára a feladatot. "
Minden illeszkedés feladat kitrigonometriázható. Ahogy kijön koordinátákkal, vektorokkal, komplex számokkal, k darab Pascal/Desargues tétel felírásával, etc.
Az enyém valamivel elemibb geometriát használ, csak sokat:
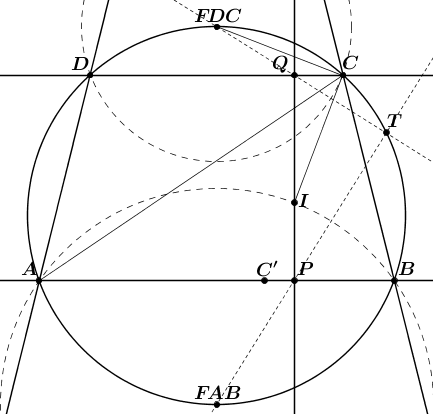
1. Először belátom, hogy k1, k2 és k egy körsoron vannak. Ezt most nem bizonyítom. Utána azt fogom belátni, hogy k2 és k (a trapéz körülírt köre) érintik egymást.
2. A Thalész-tétel értelmében ha a FAB-P és a FDC-Q egyenesek a k körön metszik egymást, akkor a PQ Thalész-köre is átmegy azon a ponton. (FAB az AB ív felezőpontja, FDC hasonlóan). Legyen FAB-P metszése k körrel T, azt akarom belátni, hogy FDC, Q és T egy egyenesen van.
3. Az ABC háromszög I beírt körének középpontja rajta a FAB kp-jú, A-n átmenő körön (ez ismert). IC Thalészkörén rajta van Q, és rajta van T is, mert egy FAB kp-jú inverzió után T képe P rajta van IC' Thalész-körén.
4. Mivel az FDC-C szakasz érinti az ITCQ kört, FDC-re vonnatkozó inverzió után a kör helyben marad, Q és T kicserélődik, tehát FDC, Q és T egy egyenesen van.
5. FAB-ra vonatkozó inverzió esetén PQT átmegy egy ponton és a képén, P-n és T-n, tehát fixkör. Az AB oldalt érintette, tehát k-t is érinti, tehát k1-et is, kész.
|
 |
| Előzmény: [825] w, 2013-06-19 12:36:28 |
|
| [825] w | 2013-06-19 12:36:28 |
 B.4551. A hiv. megoldás nem valami egyszerű, maga a feladat sokkal könnyebb. Könnyű észrevenni, hogy nincs szükségünk semmilyen új körre, hisz elég szabályos az ábra, ott vannak a párhuzamosok és merőlegesek. Átírhatjuk egy trigonometriapéldára a feladatot.
A ki kör középpontja Oi, sugara ri (i=1,2); AC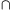 BD=M; BD=M; 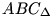 -ben a szokásos jelölések érvényesek. Elég megmutatni, hogy a két kör belülről érinti egymást, azaz O1O2=|r1-r2|. -ben a szokásos jelölések érvényesek. Elég megmutatni, hogy a két kör belülről érinti egymást, azaz O1O2=|r1-r2|.
Először is AP=AC-BC+BP=AC-BC+(AB-AP) 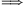 AP=(b+c-a)/2. AP=(b+c-a)/2.
Világos, hogy 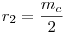 . .
Legyen M vetülete AB-re Mx, PQ-ra My. Ekkor AMx=c/2, majd MxP=AP-AMx=(b-a)/2. Nyilván My MO1, ahonnan MO1, ahonnan
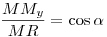 és és  , ,
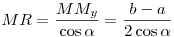 , ,
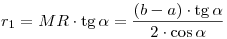 . .
Továbbá
MMx=AMx.tg  =c.tg =c.tg  /2, ezért /2, ezért
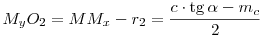 ; ;
MyO1=r1.sin  , ,
és így
O1O22=MyO12+MyO22.
Ekvivalens átalakításokkal
O1O2=|r1-r2|
O1O22=(r1-r2)2
MyO12+MyO22=r12+r22-2r1r2
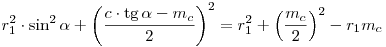

c2tg2 -2cmctg -2cmctg  +mc2=4r12cos2 +mc2=4r12cos2 +mc2-4r1mc +mc2-4r1mc


c2-2bccos  =(b-a)2-2b(b-a) =(b-a)2-2b(b-a)
c2-2bccos  =b2-2ab+a2-2b2+2ab =b2-2ab+a2-2b2+2ab
b2+c2-2bccos  =a2 =a2
Azonosság.
|
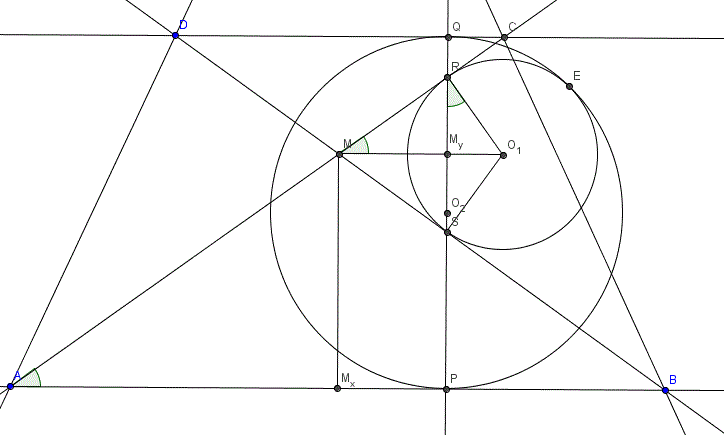 |
|
|
| [823] w | 2013-06-11 21:18:22 |
 A vége kicsit hibádzott, mert a=2-re és 3-ra is található megfelelő polinom:
p2(x)=-2x2+3x+8, ahol
p2(22/3+21/3)=-2(2.21/3+22/3+4)+3(22/3+21/3)+8=-4.21/3-2.22/3-8+3.22/3+3.21/3+8=22/3-21/3, és
p3(x)=-x2+2x+6, ahol
p3(32/3+31/3)=-3.31/3-6-32/3+2.32/3+2.31/3+6=32/3-31/3.
Az én megoldásom (elvben kicsit egyszerűbb) a következő lépésekből áll (biz. be!).
1. Kizárjuk a köbszámokat, rögzítjük a-t.
2. Az 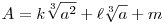 kifejezés irracionális szám, ahol k és kifejezés irracionális szám, ahol k és  nem egyszerre nulla (illetve k, nem egyszerre nulla (illetve k, ,m ,m Z). Z).
(Ez lényegében a te első lemmád.)
3. Következmény: A 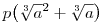 kifejezés egyértelműen előáll kifejezés egyértelműen előáll 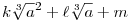 alakban (a 3. lemmád) alakban (a 3. lemmád)
4. (Ez a legfontosabb meglátás:) Legyen rögzített a és p mellett

alakú. Ekkor k  (mod (a-1)). (mod (a-1)).
(Biz.: a konstans és elsőfokú polinomokra kész vagyunk, és két ilyen polinom összege vagy szorzata is ilyen.)
5. Következmény: Világos, hogyha p(a2/3+a1/3)=a2/3-a1/3, akkor 1 -1 (mod (a-1)), tehát a-1|1-(-1)=2, és így csakis a=3,2,0,-1 lehet (kizártuk a köbszámok esetét) --> a=2,3. -1 (mod (a-1)), tehát a-1|1-(-1)=2, és így csakis a=3,2,0,-1 lehet (kizártuk a köbszámok esetét) --> a=2,3.
Pontosan azokhoz az a számokhoz létezik megfelelő p polinom, melyek egész számok köbei, vagy a=2,3.
|
| Előzmény: [822] aaaa, 2013-06-11 17:59:29 |
|



 2013-k, k>1006. De ez azt jelenti, hogy ak=1, és k darab nulla van a mondatban. Tehát ai sorozatban 2013-k darab nem nulla szám van, ezek közül kettő a1 és ak.
2013-k, k>1006. De ez azt jelenti, hogy ak=1, és k darab nulla van a mondatban. Tehát ai sorozatban 2013-k darab nem nulla szám van, ezek közül kettő a1 és ak. 

 =CBD
=CBD /2+
/2+ /2=DEF
/2=DEF


 Q(x+k) (k>0), akkor mekkora lehet k?
Q(x+k) (k>0), akkor mekkora lehet k? x,y
x,y


 BD=M;
BD=M;  AP=(b+c-a)/2.
AP=(b+c-a)/2.  MO1, ahonnan
MO1, ahonnan 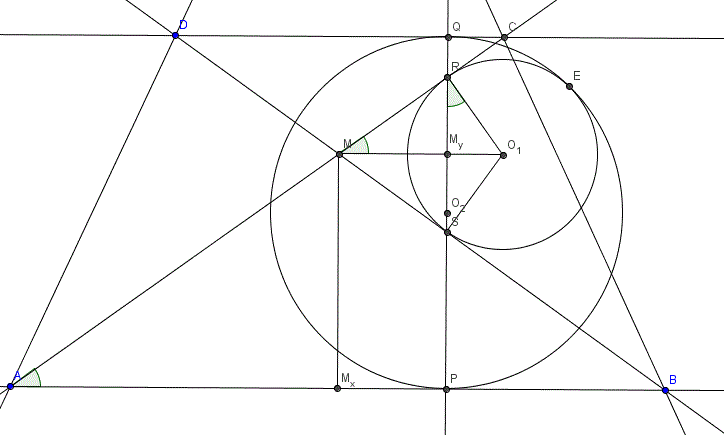
 ,
, nem egyszerre nulla (illetve k,
nem egyszerre nulla (illetve k,