|
| [884] w | 2014-06-07 23:23:01 |
 A.513. Milyen &tex;\displaystyle p&xet; prímekre van olyan harmadfokú, egész együtthatós &tex;\displaystyle f&xet; polinom, amelynek főegyütthatója nem osztható &tex;\displaystyle p&xet;-vel, és amelyre az &tex;\displaystyle f(1),f(2),...,f(p)&xet; számok páronként különböző maradékot adnak &tex;\displaystyle p&xet;-vel osztva?
Egy lehetséges megközelítés (kíváncsi vagyok, hogy van-e benne hiba, illetve hogy a kitűző erre számított-e):
Megmutatjuk, hogy ezek a prímek éppen a &tex;\displaystyle 3k+2&xet; alakúak és a &tex;\displaystyle 3&xet;.
Ha &tex;\displaystyle (p-1,3)=1&xet;, akkor az &tex;\displaystyle f(x)=x^3&xet; polinom megfelelő. Valóban, ha &tex;\displaystyle g&xet; primitív gyök modulo &tex;\displaystyle p&xet;, akkor &tex;\displaystyle g^1,\dots,g^{p-1}&xet; redukált maradékrendszer modulo &tex;\displaystyle p&xet;, ahonnan &tex;\displaystyle (p-1,3)=1&xet; miatt &tex;\displaystyle g^3,\dots,g^{3(p-1)}&xet; is redukált maradékrendszer lesz modulo &tex;\displaystyle p&xet;. Vagyis a redukált maradékrendszer köbe, így &tex;\displaystyle \{1^3,\dots,(p-1)^3\}&xet; is redukált maradékrendszer modulo &tex;\displaystyle p&xet;. Ez még a &tex;\displaystyle p^3\equiv 0&xet; maradékkal kiegészülve teljes maradékrendszert hoz létre.
Most tegyük fel, hogy van olyan &tex;\displaystyle p=3k+1&xet; prímszám és &tex;\displaystyle f(x)=ax^3+bx^2+cx+d&xet; polinom, melyre &tex;\displaystyle \{f(1),\dots,f(p)\}&xet; és &tex;\displaystyle \{1,\dots,p\}&xet; megegyezik modulo &tex;\displaystyle p&xet;, és &tex;\displaystyle (a,p)=1&xet;. Feltehető, hogy &tex;\displaystyle b&xet; és &tex;\displaystyle c&xet; sem osztható &tex;\displaystyle p&xet;-vel.*
Legyen &tex;\displaystyle g&xet; primitív gyök modulo &tex;\displaystyle p&xet;, és legyen &tex;\displaystyle r=g^k&xet;. Ekkor &tex;\displaystyle r^3=g^{3k}=g^{p-1}\equiv 1\mod p&xet; a Kis-Fermat-tétel szerint. Tekintsük azt az &tex;\displaystyle s&xet; maradékosztályt mod &tex;\displaystyle p&xet;, melyre &tex;\displaystyle b(r+1)s\equiv -c\mod p&xet;. (Ilyen létezik, hisz &tex;\displaystyle r\neq -1&xet; és &tex;\displaystyle b\neq 0&xet; mod &tex;\displaystyle p&xet;, és nem nulla, hisz &tex;\displaystyle c\neq 0&xet; mod &tex;\displaystyle p&xet;.) Ekkor
&tex;\displaystyle f(sr)-f(s)=a(s^3r^3-s^3)+b(s^2r^2-s^2)+c(sr-s)\equiv 0+bs^2(r-1)(r+1)+cs(r-1)\equiv -cs(r-1)+cs(r-1)\equiv 0\mod p,&xet;
bár &tex;\displaystyle sr\neq s&xet; mod &tex;\displaystyle p&xet;, ez tehát ellentmond a páronként inkongruens &tex;\displaystyle f&xet;-értékeknek. Így &tex;\displaystyle p=3k+1&xet; esetben nem létezik megfelelő &tex;\displaystyle f&xet; polinom. []
*Ez azért tehető fel, mert ha az &tex;\displaystyle f&xet; polinom megfelelő, akkor az
&tex;\displaystyle f(x+1)=a(x^3+3x^2+3x+1)+b(x^2+2x+1)+c(x+1)+d=ax^3+(3a+b)x^2+(3a+2b+c)x+(a+b+c+d),&xet;
&tex;\displaystyle f(x+2)=a(x^3+6x^2+12x+8)+b(x^2+4x+4)+c(x+2)+d=ax^3+(6a+b)x^2+(12a+4b+c)x+(8a+4b+2c+d)&xet;
polinomok is megfelelnek a feltételnek. Ha &tex;\displaystyle p|b&xet; volt, akkor ezekben &tex;\displaystyle x^2&xet; együtthatója relatív prím &tex;\displaystyle p&xet;-hez, és nem lehet mindkettőben &tex;\displaystyle x&xet; együtthatója &tex;\displaystyle p&xet;-vel osztható. Ha &tex;\displaystyle p|c&xet;, akkor pedig legalább egyik eltolt polinomban &tex;\displaystyle x&xet; együtthatója nem osztható &tex;\displaystyle p&xet;-vel, így ha abban &tex;\displaystyle x^2&xet; együtthatója nem osztható &tex;\displaystyle p&xet;-vel, kész, ha pedig &tex;\displaystyle p&xet;-vel osztható, akkor újra alkalmazhatjuk előbbi gondolatmenetet.
|
| Előzmény: [577] Maga Péter, 2010-10-13 09:36:25 |
|
|
| [882] w | 2014-06-07 16:10:35 |
 A.526. A síkbeli koordináta-rendszerben nevezzük sávnak az olyan tartományokat, amelyeket két párhuzamos egyenes határol. Egy sáv szélessége legyen a beleírható, a tengelyekkel párhuzamos oldalú négyzetek oldalhossza. Igazoljuk, hogy ha a &tex;\displaystyle 0\le x,y\le1&xet; egységnégyzetet lefedjük véges sok sávval, akkor ezek szélességének összege legalább 1.
Belátjuk, hogy a négyzet &tex;\displaystyle r&xet; sugarú &tex;\displaystyle k&xet; beírt körlapjának lefedéséhez is legalább &tex;\displaystyle 2r&xet; szélességösszegű sávokra van szükség.
Tekintsünk a &tex;\displaystyle k&xet; fölé írható &tex;\displaystyle G&xet; félgömböt, és feleltessük meg &tex;\displaystyle k&xet; minden &tex;\displaystyle P&xet; pontját &tex;\displaystyle G&xet; azon pontjával, aminek vetülete &tex;\displaystyle k&xet; síkján &tex;\displaystyle P&xet;. Tekintsünk tetszőleges &tex;\displaystyle d&xet; széles sávot, messük el &tex;\displaystyle k&xet;-val, és tekintsük a &tex;\displaystyle k&xet;-val közös pontjainak &tex;\displaystyle G&xet;-re eső megfeleltetettjeit. A megfeleltetett pontok egy félgömbréteget alkotnak, amelynek szélessége &tex;\displaystyle \le d&xet;. Ezen félgömbréteg felszíne tehát &tex;\displaystyle \le \pi r d&xet;.
Amennyiben a &tex;\displaystyle d_1,\dots,d_n&xet; széles sávok lefedik a teljes &tex;\displaystyle k&xet; körlapot, a sávok &tex;\displaystyle G&xet;-n lévő megfeleltetettjei lefedik a teljes &tex;\displaystyle G&xet;-t. Viszont minden &tex;\displaystyle i&xet;-re a &tex;\displaystyle d_i&xet; széles sáv legfeljebb &tex;\displaystyle \pi r d_i&xet; felszínű gömbövnek felel meg, amiért &tex;\displaystyle \sum_{i=1}^n \pi r d_i\ge A_G=2\pi r^2&xet;, leosztva &tex;\displaystyle d_1+\dots+d_n\ge 2r&xet;. Ezt akartuk belátni.
|
|
| [881] Fálesz Mihály | 2014-05-13 17:28:51 |
 Adott az &tex;\displaystyle (n+3)&xet;-dimenziós térben három vektor:
&tex;\displaystyle {\bf a}=\bigg((-1)^n\binom{n}{0};(-1)^{n-1}\binom{n}{1};
(-1)^{n-2}\binom{n}{2};
\dots;\binom{n}{n}; 0; 0 \bigg), &xet;
&tex;\displaystyle {\bf b}=\bigg(0; (-1)^n\binom{n}{0};(-1)^{n-1}\binom{n}{1};
(-1)^{n-2}\binom{n}{2};
\dots;\binom{n}{n}; 0 \bigg), &xet;
és
&tex;\displaystyle {\bf c}=\bigg(0;0; (-1)^n\binom{n}{0};(-1)^{n-1}\binom{n}{1};
(-1)^{n-2}\binom{n}{2};
\dots;\binom{n}{n} \bigg). &xet;
Határozzuk meg a &tex;\displaystyle {\bf v}&xet; vektor minimális hosszát, ha
&tex;\displaystyle {\bf a}\cdot{\bf v} = {\bf b}\cdot {\bf v} = {\bf c}\cdot {\bf v} = n!&xet;
teljesül.
|
| Előzmény: [880] w, 2014-05-13 16:30:27 |
|
| [880] w | 2014-05-13 16:30:27 |
 Köszi, ez az alapkoncepció nálam is megvolt, de nem töltöttem a feladattal elég időt, hogy kijöhessen. A két hatvány különbsége résznél megjelenő becslés már nem volt meg, az már érdekes volt.
Az A611.-re is volt néhány gondolatom. Nevezetesen ha &tex;\displaystyle \sum_{k=0}^n \binom nk p(x+k)=n!&xet;-t már tudjuk, meg még efféle azonosságokat, akkor már alkalmasan súlyozott négyzetes-számtani közepek közötti becsléssel elvileg kijön. Az első benyomás persze Csebisev-polinomok volt, de utána azok nem látszottak alkalmasnak. Előbbi sorokat viszont semmi értelme sincs beírni, mert nem vezettek megoldásra.
Úgy általában, meg voltam az ez évi pontversenyben lepve, hogy (február előtt) minden egyes A-feladatra megjelent hivatalos megoldás. Ezzel együtt furcsállom, hogy már egy ideje alig írnak ki megoldásokat a B-jelű feladatokra, a korábbi sok évvel ellentétben.
|
| Előzmény: [876] Róbert Gida, 2014-04-30 20:01:27 |
|
|
| [878] Fálesz Mihály | 2014-05-07 18:55:35 |
 Ha nem volt odaírva semmi, akkor a polinom valós együtthatós. Az abszolútérték-jelekre tényleg nincs szükség.
Btw komplex együtthatós polinomokra triviálisan ugyanaz a válasz. (Csak akkor más betűt használnánk az &tex;\displaystyle i&xet; helyett.)
|
| Előzmény: [877] Róbert Gida, 2014-05-06 19:39:15 |
|
| [877] Róbert Gida | 2014-05-06 19:39:15 |
 A611-nél (ezt sem oldotta meg senki) komplex együtthatós polinomok között kell a minimum? Csak, mert furcsa, hogy &tex;\displaystyle |p(i)|^2&xet;-ek vannak, amik valós együtthatós polinomoknál persze az absz. jel elhagyható! (és általában a Kömalnál valós együtthatós polinomok vannak, ha mást nem írnak).
|
| Előzmény: [875] w, 2014-04-30 14:17:42 |
|
| [876] Róbert Gida | 2014-04-30 20:01:27 |
 A612. érdekes feladat &tex;\displaystyle http://en.wikipedia.org/wiki/Catalan's\_conjecture&xet; és Pillai sejtés mutatja, hogy milyen nehéz (Pillai még mindig megoldatlan).
Néhány morzsa(?): természetesen végtelen sok ilyen szám van (ezt sejtjük). &tex;\displaystyle 8k+6&xet; alakú számok nem állnak elő két négyzetszám különbségeként vagy összegeként (8-cal való osztási maradékokat nézzük). Így &tex;\displaystyle N&xet;-ig tekintve a számokat &tex;\displaystyle \frac {N}{8}-1&xet; megmarad, a számok egy pozitív alsó sűrűsége. Továbbiakban feltesszük, hogy a két szám (összegénél vagy különbségénél) valamelyike nem négyzetszám. Teljes hatványok &tex;\displaystyle a^p&xet; alakban is felírhatóak, ahol &tex;\displaystyle a>1&xet; és &tex;\displaystyle p&xet; prím.
Két teljes hatvány össezegként előálló számok kevesen vannak: &tex;\displaystyle N\ge x=a^p+b^q&xet;, ahol &tex;\displaystyle p>2&xet; vagy &tex;\displaystyle q>2&xet;, akkor &tex;\displaystyle a&xet;-ra legfeljebb &tex;\displaystyle N^{\frac 1p}&xet;, míg &tex;\displaystyle b&xet;-re &tex;\displaystyle N^{\frac 1q}&xet; lehetőség van, ez összesen &tex;\displaystyle N^ {\frac 1p+\frac 1q}\le N^{\frac 56}&xet; lehetőség. Továbbá &tex;\displaystyle 2^p<N&xet; és &tex;\displaystyle 2^q<N&xet; így &tex;\displaystyle p,q<\log_2 N&xet;. Ebből &tex;\displaystyle x&xet;-re &tex;\displaystyle O(\log(N)^2*N^{\frac 56}) = o(N)&xet; lehetőség van.
A nehéz eseteket persze a két teljes hatvány különbsége okozza. Legyen &tex;\displaystyle N\ge x=a^p-b^q>0&xet; ekkor &tex;\displaystyle a>b^{\frac qp}&xet;. Itt megint kevés szám áll elő ilyen alakban, ha &tex;\displaystyle a&xet; nagy, pontosabban: &tex;\displaystyle a>b^{\frac qp}+1&xet; (azaz már csak azon eseteket kell nézni, ahol &tex;\displaystyle a=ceil(b^{\frac qp})&xet;).
Ha &tex;\displaystyle a>b^{\frac qp}+1&xet; és &tex;\displaystyle N\ge x=a^p-b^q&xet;, akkor &tex;\displaystyle N\ge (b^{\frac qp}+1)^p-b^q>p*b^{q-\frac qp}&xet; (binomiális tétel). Ha &tex;\displaystyle p=2&xet;, akkor &tex;\displaystyle q>2&xet; és &tex;\displaystyle N>b^{\frac q2}&xet;, ez legfeljebb &tex;\displaystyle N^{\frac 2q}-1&xet; lehetőség &tex;\displaystyle b&xet;-re (hiszen &tex;\displaystyle b>1&xet;); csak azon &tex;\displaystyle q&xet; értékeket kell nézni amelyekre &tex;\displaystyle N^{\frac 2q}\ge 2&xet;, innen &tex;\displaystyle q<const*\log N&xet;. Azaz &tex;\displaystyle \sum_{q=2}^ {const*\log N} (N^{\frac 2q}-1)=O(N^{\frac 23})=o(N)&xet; lehetőséget ad. Ha &tex;\displaystyle q=2&xet;, akkor &tex;\displaystyle p>2&xet; és &tex;\displaystyle N\ge p*b^{2-\frac 2p}\ge p*b^{\frac 43}&xet;, így legfeljebb s=&tex;\displaystyle \sum _{p=2}^{N} (\frac Np) ^{\frac 34}&xet; egész áll elő így (itt &tex;\displaystyle p>N&xet;-re &tex;\displaystyle x>N&xet; lenne). Integrálással és prímszámtétellel &tex;\displaystyle s=O(\frac {N}{\log N})=o(N)&xet;.
Azaz, ahogyan mondtam csak azon eset maradt vissza, amikor &tex;\displaystyle N\ge x=a^p-b^q&xet;, &tex;\displaystyle p>2&xet; vagy &tex;\displaystyle q>2&xet; és &tex;\displaystyle b=ceil(a^{\frac qp})&xet;. Ez nincs meg, lényegében arról van szó, hogy &tex;\displaystyle a^p-b^q&xet; csak úgy lehet "kicsi", ha &tex;\displaystyle b^{\frac qp}&xet; "nagyon" közel esik egy egészhez. Itt &tex;\displaystyle b^{\frac qp}&xet; vagy egész (ha &tex;\displaystyle b&xet; az &tex;\displaystyle p&xet;-edik hatvány), vagy irracionális; (itt persze az első eset könnyű, ha &tex;\displaystyle b&xet; az &tex;\displaystyle p&xet;-edik hatvány, akkor &tex;\displaystyle a^p-b^q=0&xet;).
|
| Előzmény: [875] w, 2014-04-30 14:17:42 |
|
| [875] w | 2014-04-30 14:17:42 |
 A szokástól eltérően az A.610-A.613 feladatokra nincs (még) hivatalos megoldás. Ezekre, vagy velük kapcsolatban megoldási ötletekre nagyon kíváncsi volnék.
|
|
|
| [873] Erben Péter | 2014-04-23 17:46:04 |
 B.4621: (a) A tetraéder éleit érintő gömb létezésének szükséges és elégséges feltétele: a szemközti élpárok hosszának összege egyenlő mindhárom pár esetén. (b) A külső érintőgömb létezésének szükséges és elégséges feltétele: a szemközti élpárok hosszának különbsége egyenlő. (A kivonásoknál számít a sorrend, azok az élek szerepelnek negatív előjellel, amelyek által alkotott háromszög oldalait kívülről, az élek belső pontjában érinti a gömb.)
A két feltétel együtt azzal ekvivalens, hogy három egy csúcsból induló él hossza egyenlő (&tex;\displaystyle x&xet;), és a másik három él is egyenlő (&tex;\displaystyle y&xet;).
Ha &tex;\displaystyle x \ne y&xet;, akkor a többi "hozzáírt gömb" nem létezik, vagyis a feladat állítása hamis.
Rosszul látom?
/Irodalom: Reiman-Dobos Nemzetközi Matematikai Diákolimpiák, 1962/7. feladathoz fűzött megjegyzések./
|
|
|
| [871] Fálesz Mihály | 2014-03-14 10:26:19 |
 A. 609+. Legyen A és B két körlap vagy félsík a komplex síkon, a1,a2,...,an A\B és b1,b2,...,bn A\B és b1,b2,...,bn B\A, és legyen B\A, és legyen
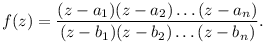
Igazoljuk, hogy az f' függvény minden gyöke az A B halmazban van. B halmazban van.
|
| Előzmény: [870] Fálesz Mihály, 2014-03-14 10:15:42 |
|
| [870] Fálesz Mihály | 2014-03-14 10:15:42 |
 A. 609. Legyenek a1,a2,...,an és b1,b2,...,bn olyan komplex számok, amelyekre Im aj 1 és Im bj 1 és Im bj -1 (j=1,2,...,n), és legyen -1 (j=1,2,...,n), és legyen
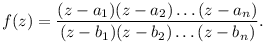
Igazoljuk, hogy az f'(z) függvénynek nincs gyöke az |Im z|<1 halmazon.
A. 480. Tegyük fel, hogy p(z) olyan n-edfokú, komplex együtthatós polinom, melynek minden (komplex) gyöke egységnyi abszolút értékű. Mutassuk meg, hogy tetszőleges c 0 valós számra a 0 valós számra a
2z(z-1)p'(z)+((c-n)z+(c+n))p(z)
polinom gyökei is egységnyi abszolút értékűek.
A. 430. Legyen n 2 és u1=1,u2,...,un legfeljebb 1 abszolút értékű komplex számok, továbbá legyen 2 és u1=1,u2,...,un legfeljebb 1 abszolút értékű komplex számok, továbbá legyen
f(x)=(x-u1)(x-u2)...(x-un).
Igazoljuk, hogy az f'(x) polinomnak létezik olyan komplex gyöke, aminek a valós része nemnegatív.
Iliev-Sendov sejtés: Ha f legalább másodfokú komplex együtthatós polinom, amelynek minden gyöke az egységkörben van, akkor az f' gyökei köré rajzolt egységkörök lefedik f gökeit.
|
| Előzmény: [869] w, 2014-03-13 22:30:32 |
|
|
| [868] w | 2014-02-12 19:55:42 |
 Bocs, azt elnéztem.
A.605 megoldása egyszerűbben, de gyengébb becslésekkel:

(számok rendezettsége)
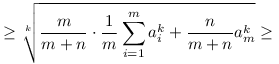
(kihasználva a rendezettséget és 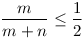 feltételt) feltételt)
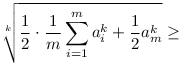
(kéttagú számtani-mértani)

(céltudatos becslés a rendezéssel)
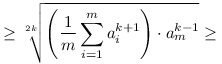
(rendezettség és k 1) 1)
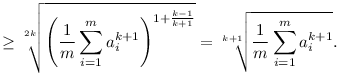
|
| Előzmény: [867] Róbert Gida, 2014-02-11 22:13:34 |
|
| [867] Róbert Gida | 2014-02-11 22:13:34 |
 "Lényegében én is így csináltam, bár kicsivel erősebb állítást láttam be, amihez nem kellett dupla indukció. Ennek ellenére teljesen más megközelítésem volt"
Kevesebbet láttál be, hiszen 2p2k+1 jóval kisebb, mint az én bizonyításomból kijövő: minden (n+1) paritásával megegyező egész előáll +-os alakban a [-sn+14,sn-14] intervallumból: trivi, hiszen, ha c előáll néhány prím összegeként, akkor +-os összegben plusszal szerepeljenek pont ezen prímek, akkor az összeg (sn-c)-c=sn-2*c, és itt c az [7,sn-7]-be esik.
Egyébként azt is meg lehet mondani, hogy milyen (lehetséges) számok maradnak ki az [-sn,sn] intervallumból, ha n>3: sn-12,sn-8,sn-2, és ezek mínusz egyszeresei, azért, mert az 1,4,6 nem állítható elő néhány prím összegeként.
|
| Előzmény: [866] w, 2014-02-11 21:13:56 |
|
| [866] w | 2014-02-11 21:13:56 |
 Lényegében én is így csináltam, bár kicsivel erősebb állítást láttam be, amihez nem kellett dupla indukció. Ennek ellenére teljesen más megközelítésem volt.
Azt látom be, hogy k 3 esetén minden -2p2k+1 és +2p2k+1 közötti páros szám előáll 3 esetén minden -2p2k+1 és +2p2k+1 közötti páros szám előáll  p1 p1 p2 p2 ... ... p2k+1 alakban. p2k+1 alakban.
Az alapeset néhány kis számolás kérdése: megkeressük k=1-re, majd k=2-re, majd k=3-ra a váltakozó előjeles összeggel előállítható számokat, és látjuk, hogy k=3-ra már jó lesz. Már itt feltűnik az az egyszerű megállapítás, hogy ha s előáll váltakozó előjelű összegként, akkor minden előjelet megcserélve, -s is előáll.
Az indukciós lépés k-1-ről k-ra megy. Ha egy  p1 p1 ... ... p2k-1 alakú számból akarunk egy p2k-1 alakú számból akarunk egy  p1 p1 ... ... p2k-1 p2k-1 p2k p2k p2k+1 alakút képezni, csak hozzá kell adnunk p2k+1 alakút képezni, csak hozzá kell adnunk  p2k p2k p2k+1-t, ezt is fogjuk tenni. A -2p2k-1 és +2p2k-1 közötti páros számokhoz hozzáadtunk p2k+1-t, ezt is fogjuk tenni. A -2p2k-1 és +2p2k-1 közötti páros számokhoz hozzáadtunk  p2k+p2k+1-et, ami ugye szintén páros. Ezzel előállítottuk egyrészt a p2k+p2k+1-et, ami ugye szintén páros. Ezzel előállítottuk egyrészt a 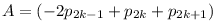 és és 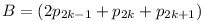 közötti páros számokat, másrészt a közötti páros számokat, másrészt a 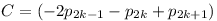 és és 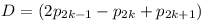 közötti páros számokat. közötti páros számokat.
A pn<2pn-1 Csebisev-tételes becslést többször használva kijön, hogy A<D, C<0, valamint B>2p2k+1. Tehát a C és D közötti páros számok tartalmazzák a 0 és A közötti páros számokat, valamint az A és B közötti páros számok tartalmazzák az A és 2p2k+1 közötti páros számokat. Tehát ezzel minden 0 és 2p2k+1 közötti páros szám előállt a váltakozó előjeles összeg alakban. Azt pedig már tárgyaltuk, hogy ekkor ellentettjeik is előálltak.
Azt az előjeles összeget választjuk, amely a nullát előállítja, ez adja a partíciót.
---
Kíváncsi volnék, milyen megközelítések lehetségesek a B.4601-re, a sajátom kicsit bonyolult volt. Emellett A.607. megoldását inverzió nélkül, ha van, megnézném.
|
| Előzmény: [865] Róbert Gida, 2014-02-11 19:41:50 |
|
| [865] Róbert Gida | 2014-02-11 19:41:50 |
 Lejárt (6 pontos!) B4600. megoldása:
b. rész: olcsó. itt az első n prím összege ptlan, így a partíció nem lehetséges.
a. rész: nehezebb, az első n prím összege ps, prímek sűrűn vannak, reménykedünk, hogy van megoldás. Partíció valóban lehetséges, sőt többet látok be. Legyen pn az n-edik prím (p1=2;p2=3;..) és sn az első n prím összege.
Állítás: ha n 5, akkor minden [7,sn-7]-be eső egész szám előáll néhány (különböző) prím összegeként az első n prímet használva. Ebből könnyen következik a feladat megoldása, hiszen, ha 5, akkor minden [7,sn-7]-be eső egész szám előáll néhány (különböző) prím összegeként az első n prímet használva. Ebből könnyen következik a feladat megoldása, hiszen, ha 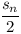 (ez egész) előáll néhány prím összegeként, akkor a kimaradók összege is (ez egész) előáll néhány prím összegeként, akkor a kimaradók összege is 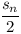 , azaz ez egy jó partíció. , azaz ez egy jó partíció.
Biz.: Az állítás könnyen ellenőrizhető n=5-re. Indukció: ha c-t szeretnénk előállítani az első n+1 prímet használva és 7 c c sn-7, akkor már az első n prímet használva is van előállítás. Ha sn-7<c sn-7, akkor már az első n prímet használva is van előállítás. Ha sn-7<c sn+1-7, akkor használjuk az n+1-edik prímet, ezzel c=pn+1+(c-pn+1), ha 7 sn+1-7, akkor használjuk az n+1-edik prímet, ezzel c=pn+1+(c-pn+1), ha 7 c-pn+1 c-pn+1 sn-7, akkor indukcióval c-pn+1-re van felbontás, amivel c egy felbontását kapjuk. Itt a felső becslés triviálisan teljesül, mert c-pn+1 sn-7, akkor indukcióval c-pn+1-re van felbontás, amivel c egy felbontását kapjuk. Itt a felső becslés triviálisan teljesül, mert c-pn+1 sn-7 ekvivalens a c sn-7 ekvivalens a c sn+1-7 feltétellel, hiszen sn+1=sn+pn+1. Az alsó becslés: 7 sn+1-7 feltétellel, hiszen sn+1=sn+pn+1. Az alsó becslés: 7 c-pn+1, de c>sn-7 feltétel volt ezzel elég belátni: 7 c-pn+1, de c>sn-7 feltétel volt ezzel elég belátni: 7 sn-6-pn+1, azaz pn+1 sn-6-pn+1, azaz pn+1 sn-13-at kell igazolni. Ez utóbbit is teljes indukcióval látom be! n=5-re teljesül, míg nagyobb n-re az indukciót használva: sn+1-13=sn+pn+1-13=(sn-13)+pn+1 sn-13-at kell igazolni. Ez utóbbit is teljes indukcióval látom be! n=5-re teljesül, míg nagyobb n-re az indukciót használva: sn+1-13=sn+pn+1-13=(sn-13)+pn+1 pn+1+pn+1=2*pn+1, azaz elég belátni, hogy 2*pn+1 pn+1+pn+1=2*pn+1, azaz elég belátni, hogy 2*pn+1 pn+2, ami Csebisev tétele miatt igaz. pn+2, ami Csebisev tétele miatt igaz.
|
|
|
| [863] w | 2014-01-13 15:51:51 |
 B.4589. megoldása komplex számokkal.
Belátjuk, hogy egész együtthatós P(x) polinomhoz és m>1 egész számhoz van olyan n, melyre a  értékek m különböző egyenlő összegű csoportra bonthatók. Legyen degP=d. értékek m különböző egyenlő összegű csoportra bonthatók. Legyen degP=d.
Legyen 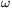 tetszőleges m-edik komplex egységgyök. Legyen továbbá s(k) a k természetes szám számjegyeinek összege az m alapú számrendszerben felírt alakjában. tetszőleges m-edik komplex egységgyök. Legyen továbbá s(k) a k természetes szám számjegyeinek összege az m alapú számrendszerben felírt alakjában.
Vezessük be a következő polinomot:
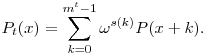
Azt állítjuk, hogy ezen polinom foka legfeljebb d-t. Mivel P0(x)=P(x), így elég megmutatni, hogy Pt+1 foka kisebb, mint Pt foka. Könnyen átgondolható, hogy

és ebből adódik, hogy Pt+1 foka legfeljebb Pt foka, továbbá Pt+1 nem tartalmaz degPt-edfokú tagot, hisz 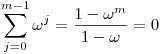 . Így a Pd+1(x) polinom már a zéruspolinom. . Így a Pd+1(x) polinom már a zéruspolinom.
Legyen
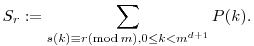
Az imént kaptuk, hogy
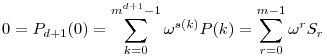
teljesül tetszőleges 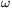 komplex m-edik egységgyökre. Ezek szerint az komplex m-edik egységgyökre. Ezek szerint az 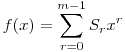 polinomnak mindegyik komplex m-edik egységgyök gyöke lesz, ebből adódóan többszöröse az xm-1+...+x+1 polinomnak, ahonnan S0=S1=...=Sm-1. Ezzel meg is adtunk egy alkalmas felbontást. polinomnak mindegyik komplex m-edik egységgyök gyöke lesz, ebből adódóan többszöröse az xm-1+...+x+1 polinomnak, ahonnan S0=S1=...=Sm-1. Ezzel meg is adtunk egy alkalmas felbontást.
|
|
|
| [861] HoA | 2013-12-19 12:59:45 |
 Nem tudom mire céloztál, úgy látom, más se. Az egyenletből kiindulva arra gondoltam, a metszéspontokra az is teljesül, mivel az egyik egyenestől 0 távolságra vannak, hogy
d1(X).d2(X)=0
. Ezért a metszéspontokra az is igaz, hogy
d12(X)+d22(X)-2.d1(X).d2(X)=(d1(X)-d2(X))2=FX2
Egy olyan koordináta-rendszerben, ahol a vezéregyenesek egyenlete y= m.x és a fókusz az x tengely pozitív értékeit tartalmazó, vezéregyenesek közti szögtartományban van, ott az előjeles távolságok különbségére egyszerű kifejezés adódik: m.x és a fókusz az x tengely pozitív értékeit tartalmazó, vezéregyenesek közti szögtartományban van, ott az előjeles távolságok különbségére egyszerű kifejezés adódik: 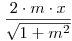 . Ezt, valamint az F fókusz (p;q) koordinátáit (d1(X)-d2(X))2=FX2 -be helyettesítve , majd még egyszer felhasználva, hogy a vezéregyeneseken lévő pontokról van szó ( y= . Ezt, valamint az F fókusz (p;q) koordinátáit (d1(X)-d2(X))2=FX2 -be helyettesítve , majd még egyszer felhasználva, hogy a vezéregyeneseken lévő pontokról van szó ( y= m.x) egy olyan másodfokú egyenletpárt kapunk x-re, melyekben a konstans tag illetve a másodfokú tag együtthatója megegyezik . Innen [856] mintájára a gyökök szorzata a két egyenletben egyenlő és így EA.EB=EC.ED is teljesül. ( A mostani m persze fele akkora szög tangense, mint a [856] – beli ) m.x) egy olyan másodfokú egyenletpárt kapunk x-re, melyekben a konstans tag illetve a másodfokú tag együtthatója megegyezik . Innen [856] mintájára a gyökök szorzata a két egyenletben egyenlő és így EA.EB=EC.ED is teljesül. ( A mostani m persze fele akkora szög tangense, mint a [856] – beli )
Vagy más volt az elképzelésed?
|
| Előzmény: [856] Fálesz Mihály, 2013-12-13 07:47:25 |
|






 A\B és b1,b2,...,bn
A\B és b1,b2,...,bn B halmazban van.
B halmazban van. 1 és Im bj
1 és Im bj -1 (j=1,2,...,n), és legyen
-1 (j=1,2,...,n), és legyen  p1
p1 , m, n
, m, n tetszőleges m-edik komplex egységgyök. Legyen továbbá s(k) a k természetes szám számjegyeinek összege az m alapú számrendszerben felírt alakjában.
tetszőleges m-edik komplex egységgyök. Legyen továbbá s(k) a k természetes szám számjegyeinek összege az m alapú számrendszerben felírt alakjában. 