|
| [1130] Berko Erzsebet | 2021-08-08 10:51:33 |
 Csináltam. Elég sok órám, napon van már ezen görbék vizsgálatában. Nemcsak ezeket a talán kúpszeletnek kinéző görbéket vizsgáltam. A nyomvonalon 5 pont kiválasztása elég bizonytalan. Most beteszem fiókba példát, de nincs elfelejtve.
|
| Előzmény: [1129] Sinobi, 2021-08-08 08:42:33 |
|
|
|
|
| [1126] Berko Erzsebet | 2021-08-08 07:00:54 |
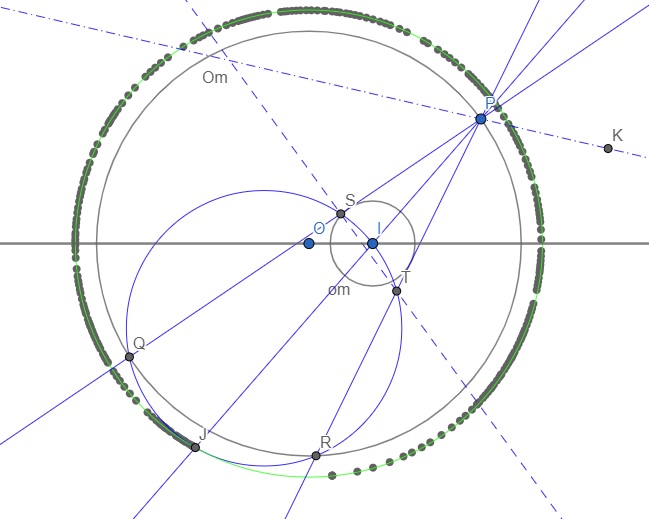
 A kicsi kör és a körérintők helyett 3 fixpontot is felvehetünk, akár nagy körön kívül is. Tehát azt vettem észre, hogy a feladatnál maradva (tehát kicsi kör a körérintőkkel) a J pontok kúpszeletet írnak le. Kúpszeleteknek van ilyen származtatása? Tehát ez a kúpszelet téma érdekelne.
|
|
| [1125] Sinobi | 2021-08-07 22:54:33 |
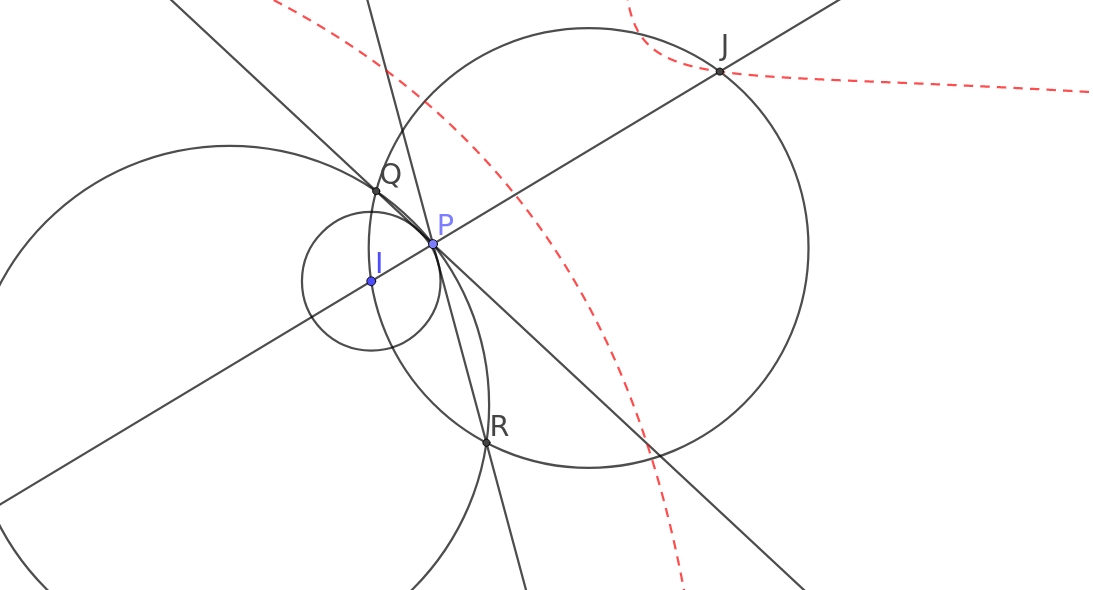
 Azt állítom, hogy a keresett pont az az I pont I' inverze az Ω körre, azaz P K I' mindig egy egyenesre esnek.
Bizonyítás: Vegyük fel P-ből azt az i inverziót, az IQR kört helyben hagyja, ez Ω-t ST-be viszi, I-t J-be.
Mivel I és I' tükrösek Ω-ra, ezért a képeik tükrösek ST-re, azaz I' képe i-nél K, ami azt jelenti, hogy P, K, I' egy egyenesre esik.
Megjegyzés: sehol nem használtam ki, hogy PQ és PR érintenek egy ω kört, tetszőleges szelők lehetnek.
|
| Előzmény: [1114] sakkmath, 2021-07-19 22:51:45 |
|
| [1124] Berko Erzsebet | 2021-08-07 19:10:00 |
 Előző hozzászólásom utolsó mondata. Eredetileg nem ezt akartam írni. Kiderítettem az okát, hogy amit korábban láttam, azt utána miért nem. I mellett is nézhetünk pontot. Nekem a nagy kör középpontja az origó, a kicsi kör középpontja az x tengelyen van. Ha I mellett úgy veszem fel a három fix pont közül az egyiket, hogy az nincs a centrálison, akkor nem a tengelyen kell várnom azt a bizonyos pontot:) Elsőre valószínű a centrálison vettem fel egy fixpontot I környezetében, utána az ellenőrzéskor, meg nem.
|
|
| [1123] Berko Erzsebet | 2021-08-07 08:21:41 |
 Van 6 pontunk egy körön. A szelőtétel miatt PS*PQ=PT*PR=PI*PJ=PI*(PM+MK), ahol ST metszet PJ=M. Lehet, hogy ez a tétel adta azt a gondolatot, hogy körérintők helyett metsző egyenesekkel foglalkozzak, ilyenkor persze már nincsenek kúpszeletek, de az a bizonyos egyenesek mintha mindig ugyanazon a ponton mennének át. Amikor a körközéppont (kis körnél) helyett egy körközéppont melletti ponttal foglalkoztam, akkor már ez nem igaz, vagyis annak szerepe van.
|
|
| [1122] Berko Erzsebet | 2021-08-06 11:10:40 |
 Vagy esetleg más középponttal. A körközéppontok elhelyezkedésétől, sugarak arányától... függően én többféle kúpszeletet el tudok képzelni. Kör, ellipszis, hiperbola... Kúpszeletek szerkesztése két fixkörrel, kétkörös szerkesztések, illetve még csak elmélkedések...
|
| Előzmény: [1121] HoA, 2021-08-06 08:26:38 |
|
| [1121] HoA | 2021-08-06 08:26:38 |
 Geogebrával vizsgálva J nyomvonalát miközben \(\displaystyle P\) végigfut \(\displaystyle \Omega\)-n , nekem úgy tűnik, az a kúpszelet egy \(\displaystyle \Omega\) -val koncentrikus kör.
|
 |
| Előzmény: [1120] Berko Erzsebet, 2021-08-06 07:05:26 |
|
| [1120] Berko Erzsebet | 2021-08-06 07:05:26 |
 A J pont mintha kúpszeleten mozogna. Tehát a J pont, nem a K.
|
|
| [1119] HoA | 2021-08-05 00:00:59 |
 A sejtés ( "A két kör középpontját összekötő egyenesen van" ) könnyen bizonyítható. Vegyünk fel \(\displaystyle \Omega\) -n egy \(\displaystyle P_1\) és egy \(\displaystyle P_2\) pontot, melyek szimmetrikusak \(\displaystyle \Omega\) és \(\displaystyle \omega\) centrálisára. A feladatban leírt alakzatokat \(\displaystyle P_1\) -hez illetve \(\displaystyle P_2\) -höz megrajzolva, azok egymás tükörképei lesznek a centrálisra, így a \(\displaystyle P_1 K_1\) és \(\displaystyle P_2 K_2\) egyenesek is. Ha tehát van a feladat állításának megfelelő pont, melyen minden \(\displaystyle PK\) egyenes áthalad, az csak \(\displaystyle P_1 K_1\) és \(\displaystyle P_2 K_2\) metszéspontja lehet. Ez pedig - ha létezik - a szimmetria miatt a centrálison van.
( A hozzászólásodban leírt metszéspont \(\displaystyle I\) -nek \(\displaystyle \Omega\) -ra vonatkozó inverze. )
|
| Előzmény: [1115] Berko Erzsebet, 2021-08-02 17:02:33 |
|
|
| [1117] Berko Erzsebet | 2021-08-03 18:49:44 |
 Szerintem a K pont többféle görbén mozoghat. (Nézzük azt az esetet, amikor a két kör nem koncentrikus. Mivel sérül a szimmetria, ezért nem tudom elképzelni, hogy kijöhet ellipszis. Inkább egy igazi tojás:) Persze, mivel ezek csak elmélkedések, akár ellipszis is kijöhet. A keresett pont I-hez van közelebb a két középpont közül.)
|
| Előzmény: [1116] Lpont, 2021-08-03 15:54:01 |
|
| [1116] Lpont | 2021-08-03 15:54:01 |
 Helyes a sejtésed, bár az én ábrámon a keresett pont nagyon messze van I-től. Nyilván a két kör helyzete és sugarainak nagysága meghatározó.
Nem tudom, hogy közelebb visz-e a megoldáshoz a tény, miszerint K pont egy ellipszisen mozog és az általad említett nagy kört érintő egyenesek érintik ezt az ellipszist is.
|
| Előzmény: [1115] Berko Erzsebet, 2021-08-02 17:02:33 |
|
| [1115] Berko Erzsebet | 2021-08-02 17:02:33 |
 A.779. Ha a két kör koncentrikus, akkor néztem olyan esetet, amikor nincs második metszéspont (pl. 1, illetve 2 egység sugarú kör). Néztem olyat is, amikor az I pont képe tengelyes tükrözés után megegyezik az eredeti ponttal: 1, illetve 3 egység sugarú kör. Most legyen a két kör nem koncentrikus. Hol van az a pont, amin átmennek az egyenesek? Csak sejtés. A két kör középpontját összekötő egyenesen van. (I ponthoz közel, szereti I pont társaságát:) Kössük össze a két középpontot, majd állítsunk merőlegest I-ben erre az egyenesre. Metszeni fogja a nagyobb sugarú kört. Ebben a pontban tekintsük az érintőt. Az érintő fogja kimetszeni a pontot a két kör középpontját összekötő egyenesből.
|
| Előzmény: [1114] sakkmath, 2021-07-19 22:51:45 |
|
| [1114] sakkmath | 2021-07-19 22:51:45 |
 A szerkesztőség nem közölte a \(\displaystyle 2020.\) \(\displaystyle májusi\) \(\displaystyle számban\) kitűzött A. 779. feladat megoldását. Talán felfrissítené a Fórumot, ha valaki feltenné a sajátját.
A. 779. Adott két rögzített kör, \(\displaystyle \Omega\) és a belsejében \(\displaystyle \omega\). Az \(\displaystyle \omega\) középpontja \(\displaystyle I\). Az \(\displaystyle \Omega\) körön mozog egy \(\displaystyle P\) pont. A \(\displaystyle P\)-ből \(\displaystyle \omega\)-hoz húzott érintők második metszéspontja \(\displaystyle \Omega\)-val \(\displaystyle Q\), illetve \(\displaystyle R\). Az \(\displaystyle IQR\) kör második metszéspontjai a \(\displaystyle PI\), \(\displaystyle PQ\) és \(\displaystyle PR\) egyenesekkel rendre \(\displaystyle J\), \(\displaystyle S\), illetve \(\displaystyle T\). A \(\displaystyle J\) tükörképe az \(\displaystyle ST\) egyenesre \(\displaystyle K\). Mutassuk meg, hogy a különböző \(\displaystyle PK\) egyenesek egy ponton mennek át.
(7 pont)
|
|
| [1113] Róbert Gida | 2021-06-08 23:38:17 |
 "Van-e valakinek olyan megoldása, amely a hivatalostól eltérő módszert alkalmaz?"
Egy old school megoldás. Legyen a konstans tag: \(\displaystyle u=\frac{71+17\sqrt{17}}{2}\).
Feltehetjük, hogy \(\displaystyle a,b,c\ge 0\). Rögzített \(\displaystyle b^4+c^4\) esetén mikor lesz legszorosabb az egyenlőtlenség? Könnyű, ekkor a bal oldal fix, míg a jobb oldalra: \(\displaystyle 2(bc)^2\le b^4+c^4\) és \(\displaystyle (b^2+c^2)^2\le 2(b^4+c^4)\)-ből látható, hogy az egyenlőtlenség jobboldalának: \(\displaystyle 4abc+a^2(b^2+c^2)+3b^2c^2\) minden tagja akkor a legnagyobb, ha \(\displaystyle b=c\), és ez el is érhető: \(\displaystyle b=c=(\frac H2)^{1/4}\) választással, ahol \(\displaystyle H=b^4+c^4\) .
Továbbiakban így feltehető \(\displaystyle c=b\) ezzel kell: \(\displaystyle 2a^4+4b^4+u\ge 4ab^2+2a^2b^2+3b^4\) rendezve kell: \(\displaystyle b^4-(4a+2a^2)b^2+(2a^4+u)\ge 0\), teljes négyzetté alakítva: \(\displaystyle G(a,b)=(b^2-(2a+a^2))^2+(a^4-4a^3-4a^2+u)\ge 0\) kell. Legyen \(\displaystyle F(a)=a^4-4a^3-4a^2+u\), ekkor \(\displaystyle F'(a)=4a^3-12a^2-8a\) ennek zérushelyei: \(\displaystyle a1=0, a23=\frac{3\pm \sqrt {17}}{2}\), itt \(\displaystyle a2<0=a1<a3\). Mivel \(\displaystyle a\ge 0\)-t kell csak vizsgálnunk: az \(\displaystyle F\) fv. szig. monoton csökken \(\displaystyle [0,a3]\) intervallumon, majd \(\displaystyle [a3,\infty)\)-n növekszik, ezért \(\displaystyle [0,\infty)\)-n a minimum \(\displaystyle a=a3\)-n van, de ott éppen kis számolással \(\displaystyle F(a)=0\) is teljesül, ebből triviálisan \(\displaystyle G(a,b)\ge 0\) ami kellett. És egyenlőség pontosan akkor teljesül [bár ezt a feladat nem kérdezte], ha \(\displaystyle a=\frac{3+\sqrt{17}}{2}, b=c=\sqrt{a^2+2a}\). Általában pedig páros soknak [esetünkben pontosan 2-nek] az előjelét megváltoztatva kapunk még egyenlőséget.
|
| Előzmény: [1112] sakkmath, 2021-06-08 16:30:53 |
|
| [1112] sakkmath | 2021-06-08 16:30:53 |
 Még valami, ismét a \(\displaystyle MAPLE\) (és a hivatalos megoldás) segítségével.
Az egyenlőtlenségben egyenlőség teljesül ezekre az (a, b, c) számhármasokra:
\(\displaystyle (p, q, q); (p, -q, -q); (-p, q, -q); (-p, -q, q).\)
Látható, hogy e számhármasokon belül páratlan sok számnak pozitív az előjele.
Van-e valakinek olyan megoldása, amely a hivatalostól eltérő módszert alkalmaz?
|
| Előzmény: [1111] sakkmath, 2021-06-08 12:19:18 |
|
|
| [1110] sakkmath | 2021-06-07 23:45:34 |
 Elírást fedeztem fel a B.4784. feladat (2016. március!!) hivatalos megoldásában.
A honlapon a megoldás befejezése: (…) és \(\displaystyle a, b, c\) számok közül páros soknak pozitív az előjele. (1)
Úgy látom, ez hibás, és (1) helyére ezt kell írni:
(…) és az \(\displaystyle a, b, c\) számok közül páratlan soknak pozitív az előjele;
vagy ezt:
(…) és az \(\displaystyle a, b, c\) számok közül páros soknak negatív az előjele.
A fentiek a Maple programmal igazolhatók. Az alábbi kép beszúrásával cáfolom (1)-et.
A kép szerinti esetben \(\displaystyle a > 0, c > 0\) és \(\displaystyle b < 0\), azaz: két számnak (páros soknak) pozitív az előjele. Mint látható, a Maple (2019) szerint a nullára redulált egyenlet helyettesítési értéke \(\displaystyle 284 + 68\sqrt{17}\), ami nem zérus! A további három eset cáfolatát mellőzöm.
Remélem, a nyomtatott KöMaL-ban a helyes szöveg szerepel…
|
 |
|
| [1109] Róbert Gida | 2021-04-17 15:30:33 |
 A lejárt B5141 megoldása, tisztán kombinatorikus úton, sokkal egyszerűbben, mint a közöltek:
\(\displaystyle S=\sum_{i=0}^n\sum_{j=i}^n \binom{n}{i}\binom{n+1}{j+1}=\sum_{i=0}^n\sum_{j=i}^n\binom{n}{i}\binom{n+1}{n-j}=\sum_{i=0}^n\sum_{k=0}^{n-i}\binom{n}{i}\binom{n+1}{k}\)
Tegyünk le egy sorba \(\displaystyle n+(n+1)=2n+1\) korongot, ezek közül válasszunk ki legfeljebb \(\displaystyle n\)-et. Ezt nyilván \(\displaystyle S\) féleképpen tehetjük meg: az első \(\displaystyle n\)-ből \(\displaystyle i\)-t, míg az \(\displaystyle n+1\)-ből \(\displaystyle k\le{n-i}\) darabot választhatunk. De trivi szimmetria mutatja, hogy ezt az összes eset felében tehetjük meg [másik felében több, mint \(\displaystyle n\)-et választanánk], azaz \(\displaystyle S=\frac{2^{2n+1}}{2}=2^{2n}\), ami kellett.
|
|
| [1108] Gömb | 2021-03-24 20:01:36 |
 Igen, igazad van! Köszönöm szépen a válaszod.
Ez olyan logikus megoldás, kár hogy nekem nem jutott eszembe :'D
Egyébként akkor azt kellett volna megsejtenem, hogy \(\displaystyle n_1\), \(\displaystyle n_2\) és \(\displaystyle n\) között valami exponenciális kapcsolat van... Mindegy, mert még így is elég messze lettem volna az igazi (rész)megoldástól.
A tanulság számomra: az új megközelítés(ek) nagyon fontos(ak).
|
|
| [1107] Erben Péter | 2021-03-24 12:28:11 |
 Ha elfogadod a hivatalos megoldásban leírt formulát helyes megoldásnak, vagyis hogy
\(\displaystyle f(n)=\frac{(2+\sqrt{3})^n+(2-\sqrt{3})^n}{2},\)
akkor csak az a kérdés, hogy adhat-e a te megközelítésed egy másik alakot ugyanerre a függvényre.
Mivel \(\displaystyle x_1\) és \(\displaystyle x_2\) konstans, \(\displaystyle n_1\cdot x_2 - n_2\cdot x_1\) egy legfeljebb másodfokú polinom, ha \(\displaystyle n_1\)-ről és \(\displaystyle n_2\)-ről felteszed, hogy másodfokú polinomok.
Látható, hogy \(\displaystyle f(n)>\frac{3^n}{2}\). Ez pedig elég nagy \(\displaystyle n\) esetén \(\displaystyle n\) bármilyen másodfokú kifejezésénél nagyobb lesz. Ezen utolsó állítás bizonyításához elég azt látni, hogy amikor \(\displaystyle n\) 1-gyel nő, akkor az \(\displaystyle f(n)\)-re adott alsó korlát háromszorozódik, míg nagy \(\displaystyle n\)-ek esetén egy másodfokú \(\displaystyle g\)-re \(\displaystyle g(n+1)\) és \(\displaystyle g(n)\) aránya közel esik 1-hez.
|
| Előzmény: [1106] Gömb, 2021-03-24 07:34:13 |
|