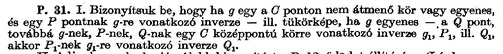| [1137] Tashi | 2021-08-14 08:57:52 |
 Proof for the problem A. 796.
For each triangle \(\displaystyle XYZ\) let \(\displaystyle \mathcal{C}_{XYZ}\) be the circumcircle of the triangle \(\displaystyle XYZ\).
Let \(\displaystyle A',\, Q',\) and \(\displaystyle P'\) be the midpoints of the segments \(\displaystyle [PQ],\,
[AP],\) and \(\displaystyle [AQ]\), respectively. Let \(\displaystyle \{H\}=PL \cap QM\) and \(\displaystyle \{H'\}=PK\cap QN\) be the orthocenters of the triangles \(\displaystyle APQ\) and \(\displaystyle CPQ\), respectively.
Let \(\displaystyle \mathcal{H}_1\) be the homothety with center \(\displaystyle A\) and ratio \(\displaystyle 1/2\). Let \(\displaystyle E_a\) be the midpoint of the segment \(\displaystyle [AH]\).
Because \(\displaystyle \{H\}=PL \cap QM\) and \(\displaystyle AL\perp LH,\, AM\perp MH\) it follows that the quadrilateral \(\displaystyle HLAM\) is cyclic. From this and \(\displaystyle ABCD\) is a cyclic quadrilateral it follows that
\(\displaystyle \measuredangle QHP=\measuredangle MHL=180^\circ-\measuredangle MAL=
180^\circ-\measuredangle BAD=\measuredangle BCD=\measuredangle QCP,\)
which implies that
\(\displaystyle
\text{the quadrilateral } HCPQ\text{ is cyclic} \tag{1}
\)
We note that \(\displaystyle \mathcal{H}_1(C)=F,\,
\mathcal{H}_1(H)=E_a,\,\mathcal{H}_1(Q)=P',\,\mathcal{H}_1(P)=Q'.\) From this and \(\displaystyle (1)\) it follows that \(\displaystyle \mathcal{H}_1(HCPQ)=E_aFQ'P'\) is a cyclic quadrilateral, which implies that \(\displaystyle F\) lies on the Euler circle (nine-point circle) \(\displaystyle \mathcal{E}_1\) if the triangle \(\displaystyle APQ\).
Because \(\displaystyle M\in \mathcal{E}_1\) and \(\displaystyle L\in \mathcal{E}_1\) it follows that
\(\displaystyle \mathcal{C}_{FLM}=\mathcal{E}_1 \tag{2}\)
Similarly to \(\displaystyle (2)\), using the homothety \(\displaystyle \mathcal{H}_2\) with center \(\displaystyle C\) and ratio \(\displaystyle 1/2\) we obtain that
\(\displaystyle
\mathcal{C}_{FKN}=\mathcal{E}_2 \tag{3}
\)
when \(\displaystyle \mathcal{E}_2\) is the Euler circle in the triangle \(\displaystyle CPQ\). Because \(\displaystyle A'\in \mathcal{E}_1\cap\mathcal{E}_2\) and \(\displaystyle A'\in PQ\), from \(\displaystyle (2)\) and \(\displaystyle (3)\) it follows that \(\displaystyle A'\in \mathcal{C}_{FLM}\cap\mathcal{C}_{FKN}\cap PQ,\) which implies the circumcircles of triangles \(\displaystyle FKN\) and \(\displaystyle FLM\), and the line \(\displaystyle PQ\) are concurrent.
|
| Előzmény: [1136] Lpont, 2021-08-13 19:19:18 |
|
| [1136] Lpont | 2021-08-13 19:19:18 |
 A 2021. márciusi A.796. feladatra van megoldása/ötlete valakinek?
|
|
| [1135] Berko Erzsebet | 2021-08-11 15:13:10 |
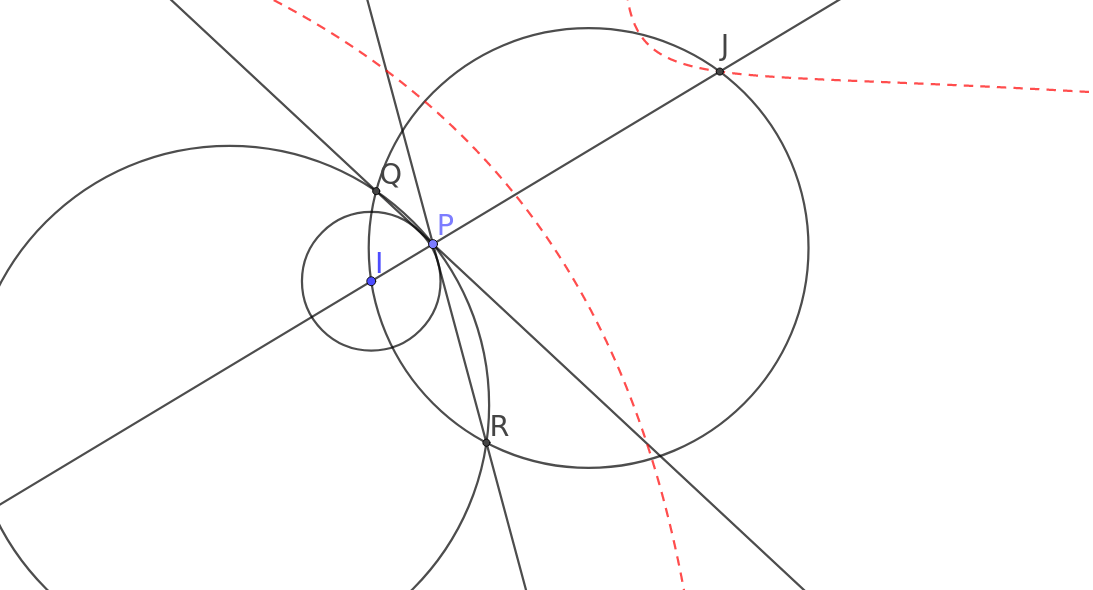
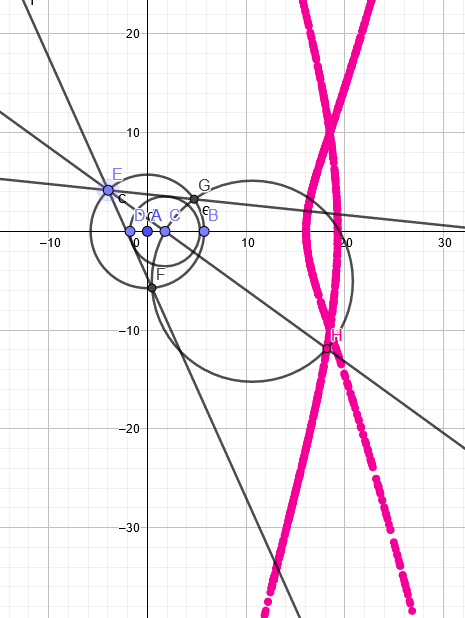
 A.779.-hez. Szemre a J pont (nálam H pont) kúpszeleten mozog. Nem ijedtem meg, hogy van olyan, hogy 2 hiperbola (?) 1-1 ága, illetve attól sem, hogy ezek metszhetik is egymást, de nem mindig metszik. Kúpszeletek származtatása? Vagy mégsem? Van köröm, csodálatos ellipszisem...
|
 |
|
| [1134] Tashi | 2021-08-09 18:43:14 |
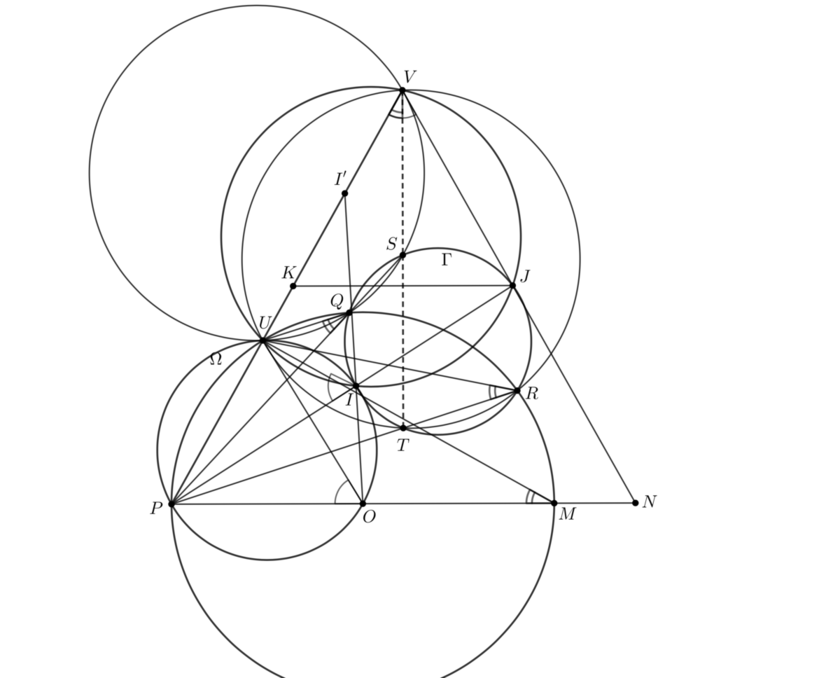
 Proof for the problem A. 779.
For a triangle \(\displaystyle XYZ\) let \(\displaystyle \mathcal{C}_{XYZ}\) be its circumcircle.
Let \(\displaystyle O\) be the center of \(\displaystyle \Omega\), \(\displaystyle \mathcal{C}_{IPO}\cap\Omega=\{P,U\}\), \(\displaystyle \mathcal{C}_{UIJ}\cap PU=\{U,V\}\), \(\displaystyle PO\cap \Omega=\{P,M\}\), \(\displaystyle VJ\cap PO=\{N\}\). Let \(\displaystyle \Gamma=\mathcal{C}_{IQR}\).
Because \(\displaystyle P\) lie on \(\displaystyle IJ\), which is the radical axis of \(\displaystyle \Gamma\) and \(\displaystyle \mathcal{C}_{UIJ}\) it follows that
\(\displaystyle PU\cdot PV= PQ\cdot PS= PT \cdot PR.\)
By Converse to power of the point it follows that
\(\displaystyle \text{ the quadrilaterals }UQSV \text{ and } UVTR \text{ are cyclic}\tag{1} \)
Because the quadrilaterals \(\displaystyle UIJV\) and \(\displaystyle POIU\) are cyclic, it follows that
\(\displaystyle \measuredangle PVN=\measuredangle UVJ=\measuredangle UIP=\measuredangle UOP.\)
From this and \(\displaystyle \measuredangle UPO=\measuredangle NPV\Rightarrow \Delta UPO\sim\Delta NPV\). From this and \(\displaystyle OP=OU\) it follows that
\(\displaystyle VP=VN\tag{2}\)
\(\displaystyle (1)\Rightarrow \measuredangle UVS=\measuredangle UQP=\measuredangle URP=\measuredangle URT=\measuredangle UVT\Rightarrow \)
\(\displaystyle V,T,S\text{ are collinear} \tag{3}\)
\(\displaystyle (1)\Rightarrow \measuredangle UVT=\measuredangle URT=\measuredangle URP=\measuredangle UMP=90^\circ-\measuredangle UPM=90^\circ-\measuredangle VPN\) \(\displaystyle \Rightarrow VT\perp PN\). From this, \(\displaystyle (1)\) and \(\displaystyle (2)\) it follows that the line \(\displaystyle V-T-S\) is \(\displaystyle V\)-height in the isosceles triangle \(\displaystyle VPN\), which implies
\(\displaystyle K\in VP\tag{4}\)
Let \(\displaystyle \psi\) be the inversion respect to the circle \(\displaystyle \Omega\) and \(\displaystyle I'=\psi(I)\). Because \(\displaystyle U, P\in \Omega\Rightarrow \psi(U)=U, \psi (P)=P\) \(\displaystyle \Rightarrow\) \(\displaystyle \psi
\left(\mathcal{C}_{UPO}\right)={PU}={PV}\) (as lines). From this and \(\displaystyle I'=\psi(I)\in
\psi\left(\mathcal{C}_{UPO}\right)\) it follows that \(\displaystyle I'\in PV\). From this and \(\displaystyle (4)\) it follows that \(\displaystyle I'\in PK\). Because \(\displaystyle I'\) is a fixed point, the problem is solved!
Remark. If I'm not mistaken, the condition that \(\displaystyle PQ\) and \(\displaystyle PR\) are tangent to \(\displaystyle \omega\) is superfluous.
|
 |
|
| [1133] HoA | 2021-08-09 01:00:14 |
 Lényegében ugyanez a megoldás adódik csak más logikai sorrendben, ha a feladatot az 1969/4 számban megjelent P. 31. problémában bizonyítandó tétel egy alkalmazásának tekintjük. Ide másolom, hogy ne kelljen keresgélni.
Ha az ottani \(\displaystyle g\) egyenesnek a mi \(\displaystyle ST\) egyenesünket, \(\displaystyle P\)-nek és \(\displaystyle Q\) -nak \(\displaystyle J\)-t illetve \(\displaystyle K\)-t, az inverzió alapkörének a \(\displaystyle P\) középpontú, \(\displaystyle IQR\) kört helyben hagyó kört feleltetjük meg, akkor \(\displaystyle g_1\) -nek \(\displaystyle \Omega\), \(\displaystyle P_1\) -nek \(\displaystyle J\) inverze, \(\displaystyle I\) , \(\displaystyle Q_1\)-nek \(\displaystyle K\) inverze, - a \(\displaystyle PK\) egyenes \(\displaystyle K'\) pontja - felel meg és a tétel éppen azt mondja ki, hogy ekkor \(\displaystyle I\) nek \(\displaystyle \Omega\)-ra vonatkozó inverze \(\displaystyle K'\).
|
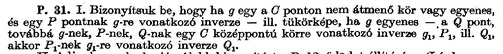 |
| Előzmény: [1125] Sinobi, 2021-08-07 22:54:33 |
|
|
|
| [1130] Berko Erzsebet | 2021-08-08 10:51:33 |
 Csináltam. Elég sok órám, napon van már ezen görbék vizsgálatában. Nemcsak ezeket a talán kúpszeletnek kinéző görbéket vizsgáltam. A nyomvonalon 5 pont kiválasztása elég bizonytalan. Most beteszem fiókba példát, de nincs elfelejtve.
|
| Előzmény: [1129] Sinobi, 2021-08-08 08:42:33 |
|
|
|
|
| [1126] Berko Erzsebet | 2021-08-08 07:00:54 |
 A kicsi kör és a körérintők helyett 3 fixpontot is felvehetünk, akár nagy körön kívül is. Tehát azt vettem észre, hogy a feladatnál maradva (tehát kicsi kör a körérintőkkel) a J pontok kúpszeletet írnak le. Kúpszeleteknek van ilyen származtatása? Tehát ez a kúpszelet téma érdekelne.
|
|
| [1125] Sinobi | 2021-08-07 22:54:33 |
 Azt állítom, hogy a keresett pont az az I pont I' inverze az Ω körre, azaz P K I' mindig egy egyenesre esnek.
Bizonyítás: Vegyük fel P-ből azt az i inverziót, az IQR kört helyben hagyja, ez Ω-t ST-be viszi, I-t J-be.
Mivel I és I' tükrösek Ω-ra, ezért a képeik tükrösek ST-re, azaz I' képe i-nél K, ami azt jelenti, hogy P, K, I' egy egyenesre esik.
Megjegyzés: sehol nem használtam ki, hogy PQ és PR érintenek egy ω kört, tetszőleges szelők lehetnek.
|
| Előzmény: [1114] sakkmath, 2021-07-19 22:51:45 |
|
| [1124] Berko Erzsebet | 2021-08-07 19:10:00 |
 Előző hozzászólásom utolsó mondata. Eredetileg nem ezt akartam írni. Kiderítettem az okát, hogy amit korábban láttam, azt utána miért nem. I mellett is nézhetünk pontot. Nekem a nagy kör középpontja az origó, a kicsi kör középpontja az x tengelyen van. Ha I mellett úgy veszem fel a három fix pont közül az egyiket, hogy az nincs a centrálison, akkor nem a tengelyen kell várnom azt a bizonyos pontot:) Elsőre valószínű a centrálison vettem fel egy fixpontot I környezetében, utána az ellenőrzéskor, meg nem.
|
|
| [1123] Berko Erzsebet | 2021-08-07 08:21:41 |
 Van 6 pontunk egy körön. A szelőtétel miatt PS*PQ=PT*PR=PI*PJ=PI*(PM+MK), ahol ST metszet PJ=M. Lehet, hogy ez a tétel adta azt a gondolatot, hogy körérintők helyett metsző egyenesekkel foglalkozzak, ilyenkor persze már nincsenek kúpszeletek, de az a bizonyos egyenesek mintha mindig ugyanazon a ponton mennének át. Amikor a körközéppont (kis körnél) helyett egy körközéppont melletti ponttal foglalkoztam, akkor már ez nem igaz, vagyis annak szerepe van.
|
|
| [1122] Berko Erzsebet | 2021-08-06 11:10:40 |
 Vagy esetleg más középponttal. A körközéppontok elhelyezkedésétől, sugarak arányától... függően én többféle kúpszeletet el tudok képzelni. Kör, ellipszis, hiperbola... Kúpszeletek szerkesztése két fixkörrel, kétkörös szerkesztések, illetve még csak elmélkedések...
|
| Előzmény: [1121] HoA, 2021-08-06 08:26:38 |
|
| [1121] HoA | 2021-08-06 08:26:38 |
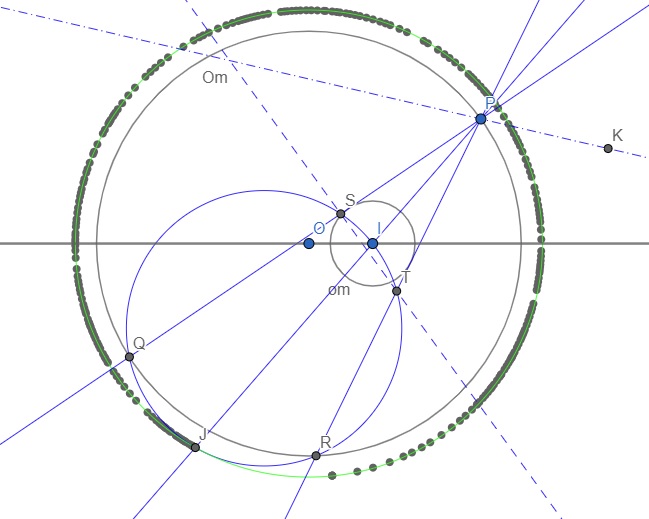
 Geogebrával vizsgálva J nyomvonalát miközben \(\displaystyle P\) végigfut \(\displaystyle \Omega\)-n , nekem úgy tűnik, az a kúpszelet egy \(\displaystyle \Omega\) -val koncentrikus kör.
|
 |
| Előzmény: [1120] Berko Erzsebet, 2021-08-06 07:05:26 |
|
| [1120] Berko Erzsebet | 2021-08-06 07:05:26 |
 A J pont mintha kúpszeleten mozogna. Tehát a J pont, nem a K.
|
|
| [1119] HoA | 2021-08-05 00:00:59 |
 A sejtés ( "A két kör középpontját összekötő egyenesen van" ) könnyen bizonyítható. Vegyünk fel \(\displaystyle \Omega\) -n egy \(\displaystyle P_1\) és egy \(\displaystyle P_2\) pontot, melyek szimmetrikusak \(\displaystyle \Omega\) és \(\displaystyle \omega\) centrálisára. A feladatban leírt alakzatokat \(\displaystyle P_1\) -hez illetve \(\displaystyle P_2\) -höz megrajzolva, azok egymás tükörképei lesznek a centrálisra, így a \(\displaystyle P_1 K_1\) és \(\displaystyle P_2 K_2\) egyenesek is. Ha tehát van a feladat állításának megfelelő pont, melyen minden \(\displaystyle PK\) egyenes áthalad, az csak \(\displaystyle P_1 K_1\) és \(\displaystyle P_2 K_2\) metszéspontja lehet. Ez pedig - ha létezik - a szimmetria miatt a centrálison van.
( A hozzászólásodban leírt metszéspont \(\displaystyle I\) -nek \(\displaystyle \Omega\) -ra vonatkozó inverze. )
|
| Előzmény: [1115] Berko Erzsebet, 2021-08-02 17:02:33 |
|
|
| [1117] Berko Erzsebet | 2021-08-03 18:49:44 |
 Szerintem a K pont többféle görbén mozoghat. (Nézzük azt az esetet, amikor a két kör nem koncentrikus. Mivel sérül a szimmetria, ezért nem tudom elképzelni, hogy kijöhet ellipszis. Inkább egy igazi tojás:) Persze, mivel ezek csak elmélkedések, akár ellipszis is kijöhet. A keresett pont I-hez van közelebb a két középpont közül.)
|
| Előzmény: [1116] Lpont, 2021-08-03 15:54:01 |
|
| [1116] Lpont | 2021-08-03 15:54:01 |
 Helyes a sejtésed, bár az én ábrámon a keresett pont nagyon messze van I-től. Nyilván a két kör helyzete és sugarainak nagysága meghatározó.
Nem tudom, hogy közelebb visz-e a megoldáshoz a tény, miszerint K pont egy ellipszisen mozog és az általad említett nagy kört érintő egyenesek érintik ezt az ellipszist is.
|
| Előzmény: [1115] Berko Erzsebet, 2021-08-02 17:02:33 |
|
| [1115] Berko Erzsebet | 2021-08-02 17:02:33 |
 A.779. Ha a két kör koncentrikus, akkor néztem olyan esetet, amikor nincs második metszéspont (pl. 1, illetve 2 egység sugarú kör). Néztem olyat is, amikor az I pont képe tengelyes tükrözés után megegyezik az eredeti ponttal: 1, illetve 3 egység sugarú kör. Most legyen a két kör nem koncentrikus. Hol van az a pont, amin átmennek az egyenesek? Csak sejtés. A két kör középpontját összekötő egyenesen van. (I ponthoz közel, szereti I pont társaságát:) Kössük össze a két középpontot, majd állítsunk merőlegest I-ben erre az egyenesre. Metszeni fogja a nagyobb sugarú kört. Ebben a pontban tekintsük az érintőt. Az érintő fogja kimetszeni a pontot a két kör középpontját összekötő egyenesből.
|
| Előzmény: [1114] sakkmath, 2021-07-19 22:51:45 |
|
| [1114] sakkmath | 2021-07-19 22:51:45 |
 A szerkesztőség nem közölte a \(\displaystyle 2020.\) \(\displaystyle májusi\) \(\displaystyle számban\) kitűzött A. 779. feladat megoldását. Talán felfrissítené a Fórumot, ha valaki feltenné a sajátját.
A. 779. Adott két rögzített kör, \(\displaystyle \Omega\) és a belsejében \(\displaystyle \omega\). Az \(\displaystyle \omega\) középpontja \(\displaystyle I\). Az \(\displaystyle \Omega\) körön mozog egy \(\displaystyle P\) pont. A \(\displaystyle P\)-ből \(\displaystyle \omega\)-hoz húzott érintők második metszéspontja \(\displaystyle \Omega\)-val \(\displaystyle Q\), illetve \(\displaystyle R\). Az \(\displaystyle IQR\) kör második metszéspontjai a \(\displaystyle PI\), \(\displaystyle PQ\) és \(\displaystyle PR\) egyenesekkel rendre \(\displaystyle J\), \(\displaystyle S\), illetve \(\displaystyle T\). A \(\displaystyle J\) tükörképe az \(\displaystyle ST\) egyenesre \(\displaystyle K\). Mutassuk meg, hogy a különböző \(\displaystyle PK\) egyenesek egy ponton mennek át.
(7 pont)
|
|
| [1113] Róbert Gida | 2021-06-08 23:38:17 |
 "Van-e valakinek olyan megoldása, amely a hivatalostól eltérő módszert alkalmaz?"
Egy old school megoldás. Legyen a konstans tag: \(\displaystyle u=\frac{71+17\sqrt{17}}{2}\).
Feltehetjük, hogy \(\displaystyle a,b,c\ge 0\). Rögzített \(\displaystyle b^4+c^4\) esetén mikor lesz legszorosabb az egyenlőtlenség? Könnyű, ekkor a bal oldal fix, míg a jobb oldalra: \(\displaystyle 2(bc)^2\le b^4+c^4\) és \(\displaystyle (b^2+c^2)^2\le 2(b^4+c^4)\)-ből látható, hogy az egyenlőtlenség jobboldalának: \(\displaystyle 4abc+a^2(b^2+c^2)+3b^2c^2\) minden tagja akkor a legnagyobb, ha \(\displaystyle b=c\), és ez el is érhető: \(\displaystyle b=c=(\frac H2)^{1/4}\) választással, ahol \(\displaystyle H=b^4+c^4\) .
Továbbiakban így feltehető \(\displaystyle c=b\) ezzel kell: \(\displaystyle 2a^4+4b^4+u\ge 4ab^2+2a^2b^2+3b^4\) rendezve kell: \(\displaystyle b^4-(4a+2a^2)b^2+(2a^4+u)\ge 0\), teljes négyzetté alakítva: \(\displaystyle G(a,b)=(b^2-(2a+a^2))^2+(a^4-4a^3-4a^2+u)\ge 0\) kell. Legyen \(\displaystyle F(a)=a^4-4a^3-4a^2+u\), ekkor \(\displaystyle F'(a)=4a^3-12a^2-8a\) ennek zérushelyei: \(\displaystyle a1=0, a23=\frac{3\pm \sqrt {17}}{2}\), itt \(\displaystyle a2<0=a1<a3\). Mivel \(\displaystyle a\ge 0\)-t kell csak vizsgálnunk: az \(\displaystyle F\) fv. szig. monoton csökken \(\displaystyle [0,a3]\) intervallumon, majd \(\displaystyle [a3,\infty)\)-n növekszik, ezért \(\displaystyle [0,\infty)\)-n a minimum \(\displaystyle a=a3\)-n van, de ott éppen kis számolással \(\displaystyle F(a)=0\) is teljesül, ebből triviálisan \(\displaystyle G(a,b)\ge 0\) ami kellett. És egyenlőség pontosan akkor teljesül [bár ezt a feladat nem kérdezte], ha \(\displaystyle a=\frac{3+\sqrt{17}}{2}, b=c=\sqrt{a^2+2a}\). Általában pedig páros soknak [esetünkben pontosan 2-nek] az előjelét megváltoztatva kapunk még egyenlőséget.
|
| Előzmény: [1112] sakkmath, 2021-06-08 16:30:53 |
|