| [72] Gubbubu | 2006-09-11 11:29:04 |
 Bocs, kicsit megint pongyola voltam. C-vel eredetileg a hányadost jelöltem, az előző hozzászólásomban meg a hányados szuprémumát. Az eredeti hozzászólásomban lehetne "Cn" konstanst írni "C konstans" helyett.
|
| Előzmény: [71] Gubbubu, 2006-09-11 11:25:59 |
|
| [71] Gubbubu | 2006-09-11 11:25:59 |
 Bocs, kicsit pongyola voltam, a TEX-et már elfelejtettem. S(pn)-en azt értettem, S(p1,p2,...,pn).
A második megjegyzésed én nem értem, de lehetséges, hogy egy másik problémát oldasz meg, mint az én kérdésem, ugyanis én p1,...,pn-nel nem az első n darab prím sorozatát jelöltem, hanem tetszőleges, bár különböző n darab prímszámot.
Ha neked van igazad, akkor nagy n-ekre a C hányadosnak a végtelenbe kellene tartania, haegyre nagyobb n-t veszek, nem?
Én viszont úgy látom, hogy minél nagyobb n-t veszek, egyre csökken, mégpedig egyelőre 1-hez tart.
Érdekes, mert te, azaz a mathworld link ugyanis egy részhalmazát veszi a 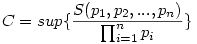 kibővített valós számot definiáló halmaznak (a szuprémum-operátor argumentumának). Mégpedig azt a részhalmazát, ahol minden prím egy speciális sorozat első néhány eleme. Na mármost, ha egy részhalmazt tekintünk, akkor annak a szuprémuma kisebb mint a bővebbé. Így az általad adott link tartalmából és a te előző megjegyzésedből következően, a "kisebb halmaz" szuprémuma végtelen, akkor viszont ha tetszőleges prímeket válszthatunk, bővebb lesz az argumentum-halmaz, és ugye (nagyobb halmaz szuprémuma nagyobb), a szuprémum is nő; vagyis az én kérdésemre is "végtelen" a válasz, azaz az eredeti kérdésemre, valóban "igaz" a válasz. kibővített valós számot definiáló halmaznak (a szuprémum-operátor argumentumának). Mégpedig azt a részhalmazát, ahol minden prím egy speciális sorozat első néhány eleme. Na mármost, ha egy részhalmazt tekintünk, akkor annak a szuprémuma kisebb mint a bővebbé. Így az általad adott link tartalmából és a te előző megjegyzésedből következően, a "kisebb halmaz" szuprémuma végtelen, akkor viszont ha tetszőleges prímeket válszthatunk, bővebb lesz az argumentum-halmaz, és ugye (nagyobb halmaz szuprémuma nagyobb), a szuprémum is nő; vagyis az én kérdésemre is "végtelen" a válasz, azaz az eredeti kérdésemre, valóban "igaz" a válasz.
Most már csak azt nem értem, hogy hogy egyeztethető össze mindez az empirikus számításaimmal, melyek szerint C csökken, ha egyre növelem az n-t.
|
| Előzmény: [70] nadorp, 2006-09-11 10:43:15 |
|
| [70] nadorp | 2006-09-11 10:43:15 |
 Bocs, de két dolgot nem értek.
Az első: Mit jelent az S(pn) jelölés ?
A második: idézet Tőled "Igaz-e, hogy bármely C konstanshoz található olyan n, hogy valamely p1, ... , pn prímekre S(p1,...,pn)>Cp1p2...pn?". Erre a válaszom igenlő, hiszen tetszőleges C-re van olyan n, hogy ln pn megfelelően nagy.
|
| Előzmény: [69] Gubbubu, 2006-09-11 10:28:04 |
|
| [69] Gubbubu | 2006-09-11 10:28:04 |
 Hú, nagy vagy! Az első két azonosságról meggyőződtem, de abban nem vagyok biztos, hogy a link az én problémámról szól (azért az is nagy segítség, hogy a probléma nem biztosan oldható meg elemien). A mathworld-link ugyanis az n-edik prímszám sorozatáról beszél, míg nálam a prímek nem feltétlenül szomszédosak a sorozatban, hanem tetszőlegesen választhatóak ki a pn sorozatból. Ez szerintem megváltoztathatja a határértéket. És valóban: néhány numerikus példa (az eddigi legnagyobb n=4, a prímek pedig 101, 449, 1327 és 7577) alapján az a sejtésem, hogy 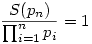 ha n -> végtelen, vagyis az eredeti kérdésre a válasz "nem igaz", és akárhogy válasszunk is, a C=1 (vagy esetleg, egy ennél kisebb) konstanst n növekedtével már nem haladhatjuk meg. A másik sejtésem az, hogy amennyiben az első sejtésem igaz, akkor tökmindegy, hogy prímekről vagy tetszőleges egész számokról van-e szó. ha n -> végtelen, vagyis az eredeti kérdésre a válasz "nem igaz", és akárhogy válasszunk is, a C=1 (vagy esetleg, egy ennél kisebb) konstanst n növekedtével már nem haladhatjuk meg. A másik sejtésem az, hogy amennyiben az első sejtésem igaz, akkor tökmindegy, hogy prímekről vagy tetszőleges egész számokról van-e szó.
|
| Előzmény: [68] nadorp, 2006-09-11 09:33:56 |
|
|
| [67] Gubbubu | 2006-09-09 18:34:42 |
 Módosítok: Vegyünk n darab különböző prímet (ha nem alkalmazzuk a megkötést, hogy a p-k prímek legyenek, talán az ios érdekes feladat, de engem a prímek jobban érdekelnének).
|
| Előzmény: [66] Gubbubu, 2006-09-09 18:33:18 |
|
| [66] Gubbubu | 2006-09-09 18:33:18 |
 Vegyünk n darab különböző számot, és képezzük belőlük az összes lehetséges j-tagú szorzatot, ahol j a 0 és az n közé vesik (nem-szigorúan kisebb mint n, és nagyobb, mint 0), majd ezeket adjuk össze. Legyenek a prímek p1,p2,...pn, és jelöljük az így kapott összeget S(p1,p2,...,pn)-nel!
Pl. 2, 3 és 11-re S(2,3,11)=1+2+3+11+6+22+33+66 = (144, ha jól számoltam)
Igaz-e, hogy bármely C konstanshoz található olyan n, hogy valamely p1, ... , pn prímekre S(p1,...,pn)>Cp1p2...pn?
Ha jól látom, szemléletesen ezt úgy lehetne megfogalmazni, hogy elegendő sok prímet véve a belőlük képezett összes szorzatok összege sokszorosa lesz a szorzatuknak.
Ha valaki valami irodalmat mellékel, az is megfelelő válasz lenne.
|
|
|
| [64] Lóczi Lajos | 2006-05-09 10:43:35 |
 Pl. a (33)-as jobb oldalán szereplő függvényhez üssük fel a függvényenciklopédiát:
http://functions.wolfram.com/HypergeometricFunctions/Hypergeometric4F3/02/
Itt mindent megtalálsz róla. A definícióban szereplő (.)k ún. emelkedő faktoriálisokat pedig itt találod:
http://functions.wolfram.com/GammaBetaErf/Pochhammer/02/
|
| Előzmény: [63] V Laci, 2006-05-08 22:06:20 |
|
| [63] V Laci | 2006-05-08 22:06:20 |
 Bocsánat, hogy picit pontatlan voltam, általános megoldóképletre gondoltam, hogy az nincs :) Nagyjából értem ezt a végtelen összegek alakot, de pl. a (33)-(35) mit jelentenek?
|
| Előzmény: [60] Lóczi Lajos, 2006-05-08 18:54:00 |
|
| [62] Lóczi Lajos | 2006-05-08 21:26:58 |
 L. pl. az idézett mathworld-oldalon a (37)-(41) formulákat, melyek hipergeometrikus sorokkal adják meg a megoldást. (Ezzel kapcsolatban össze is állítottam egy kis irományt, ami előbb-utóbb megjelenik, ott szelidített formában összefoglaltam ezeket.)
|
| Előzmény: [61] ágica, 2006-05-08 21:03:53 |
|
|
| [60] Lóczi Lajos | 2006-05-08 18:54:00 |
 Az állításod ebben a formában nem igaz, különféle megoldóképletek igenis vannak az ötödfokú egyenletre, csak azok nem "olyanok", mint a "szokásosak": nem véges, hanem végtelen sok műveletet tartalmaznak (pl. rekurziók határértékeként, vagy végtelen összegek alakban állítják elő az együtthatókból a megoldásokat -- tehát az analízis eszköztárát használják, nem pedig az algebráét).
Amire gondoltál, az persze igaz, véges sok alapművelet és véges sok gyökvonás segítségével általában nem állíthatók elő az ötödfokú egyenlet megoldásai az együtthatókból. (Speciális esetekben azonban igen, l. pl. az x5=1 egyenletet, de vannak nemtriviális példák is.) Az okokat a csoportelmélet keretén belül a Galois-elmélet válaszolja meg rendesen, a felhasznált fogalmak viszont olyanok, hogy egy ilyen kis szövegdobozban szerintem nem lehetne őket elmagyarázni (az egyetemi előadásokon több hetet szokott igénybe venni), bár ha valaki megpróbálja, kíváncsian elolvasom :) Inkább az interneten keress rá ezekre a fogalmakra, onnan sok mindent el tudsz lesni. Kiindulásul javaslom a http://mathworld.wolfram.com/QuinticEquation.html oldalt.
|
| Előzmény: [59] V Laci, 2006-05-08 15:03:21 |
|
| [59] V Laci | 2006-05-08 15:03:21 |
 Köszönöm. Úgy tudom, hogy ötödfokú és ennél nagyobb egyenletekre nem találtak megoldóképletet, és nem is találhatnak, mert bebizonyították, hogy nem is lehet. Mi ennek az oka, hogy nincs megoldóképlet?
|
| Előzmény: [57] Lóczi Lajos, 2006-05-07 23:08:31 |
|
| [58] Gergo73 | 2006-05-08 06:45:27 |
 A 2. kérdésedre valóban "nincs" a válasz. A bizonyítás nehéz és ebben a hónapban jelent meg a világ legjobb matematikai újságjában (ugyanott, ahol a Fermat-sejtés bizonyítása is, valójában a két bizonyítás nem független egymástól). Itt a cikk.
|
| Előzmény: [40] Yegreg, 2005-10-31 15:56:49 |
|
| [57] Lóczi Lajos | 2006-05-07 23:08:31 |
 Egy jó elemzés található pl. a http://mathworld.wolfram.com/CubicFormula.html címen. Maga a formula (53)-(55) alatt van. (Ha jó a szemed, épp ilyen szerkezetű kifejezéseket találsz a negyedfokú egyenlet megoldóképletében, hiszen a negyedfokú egyenlet megoldása alkalmas harmadfokú egyenlet (az ún. harmadfokú rezolvens) megoldására vezethető vissza. Persze mindezen képletetek gyakorlatilag feleslegesek, mert használhatatlanul bonyolultak.)
|
| Előzmény: [56] V Laci, 2006-05-07 22:07:14 |
|
| [56] V Laci | 2006-05-07 22:07:14 |
 Hát extrém... De akkor engem meg az érdekelne, hogy a harmadfokú egyenlet megoldóképlete hogy néz ki? (Elvileg fogjuk tanulni, de csak két év múlva, én meg nem találtam sehol...)
|
|
| [55] Lóczi Lajos | 2006-05-07 20:33:05 |
 A megadott képletek annyiban hiányosak, hogy bizonyos együttható-kombinációk esetén értelmetlenek: nullával osztás történik. Ilyenkor azonban picit más, egyszerűbb, képletek állnak rendelkezésre.
|
| Előzmény: [54] ágica, 2006-05-05 21:50:26 |
|
|
| [53] Carlos | 2006-05-05 21:00:15 |
 Tudja valaki a negyedfokú egyenlet megoldóképletét? Módszert tudok rá, hogy hogyan lehetne megoldani, de sehol sem találom azt a képletet, amiből az együtthatók segítségével egyből megkapjuk a gyököket. Azt rengeteg helyen olvasom, hogy van, csak ezt nem hogy mi is az. Ha valaki tudja, légyszi írja meg. Köszike
|
|
|
|
|
|
| [48] Tibi | 2005-11-02 20:55:55 |
 Talán még így sem tökéletes... Tehát y és x különbsége nagyobb, mint: x-nek vesszük az n-1-edik gyökét. ebből kivonunk egyet ezt az egészet szorozzuk x-szel. Na, így már tuti érthető... Még egyszer ezer bocs.
|
|
