|
| [9] lorantfy | 2003-12-02 14:11:11 |
 Kedves Fórumosok!
Nézzetek be ide is mert kihal a téma!
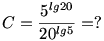
|
|
| [8] Suhanc | 2003-11-27 18:03:42 |
 Igen, tényleg elírtam! Nem szerencsés:(
|
|
| [7] lorantfy | 2003-11-26 22:04:42 |
 Kedves Suhanc!
Szépen elvagyunk itt ketten ebben a témában. Beírok egy megoldást - de szerintem elírtad a 4c2-et!
2. feladat megoldása: Belátjuk, hogy
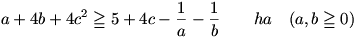
A 4c2-ből és a 4c-ből látszik, hogy bal oldalon egy különbség négyzete lesz, amihez kell még, hogy mindkét oldalhoz 1-et adjunk:
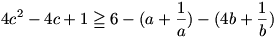
Jobb oldalon a jól ismert egyenlőtlenség:
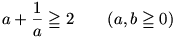
és a második tag is ilyen lesz, ha kiemelünk 2-t:

|
| Előzmény: [1] Suhanc, 2003-11-23 19:04:38 |
|
| [6] Suhanc | 2003-11-26 18:24:56 |
 Hahó!
Szakkörön kaptunk két érdekes feladatot, a témakört nem árulom el, elég könnyen kiderül. Az egyik tényleg villámkérdés, a másikról a szakkörvezető ennyit mondott: "aki ismeri a trükköt, annak trivi, aki még nem, annak lesz min gondolkodnia" :)
4. Bizonyítsuk be, hogy tekintve 2 ; 3; és 5 n. hatványainak összegét, van olyan két szám, melyek különbsége osztható 1237-tel. (ígérem, nemsokára megtanulom a képletszerkesztést)
5. Tekintsünk 512 egész számot! Bizonyítsuk be, hogy ki tudunk választani közülük néhányat, hogy összegük 512-vel osztható legyen! (leglább 1-et választunk ki, de akár az összeset is)
|
|
| [5] lorantfy | 2003-11-26 14:57:05 |
 Kedves Suhanc!
Jól gondolod, pont a sarokház az ellenpélda a b)-nél.
A d)-nél szigorú értelemben igazad van. De ha azt mondjuk, hogy testvérek azok, akiknek legalább egyik szülője közös, akkor már nem.
Szóval tágabb értelemben egyik sem tranzitív.
|
| Előzmény: [4] Suhanc, 2003-11-25 20:16:51 |
|
| [4] Suhanc | 2003-11-25 20:16:51 |
 Kedves Lórántfy!
Ha valóban ennyire "nagy" az érdeklődés, akkor én is leírom a 3. feladatra az ötleteimet.
d)nyilván tranzitív. c) Nem tranzitív./sajnos a suli számos ellenpéldát hoz a tranzitivitásra :( /
a) ha A és B szomszédok, valamint B és C szomszédok, úgy A és C B két oldalán laknak, így nem lehetnek szomszédok (eltekintve egy olyan speciális elhelyezéstől, amelyben a 3 házat egy kör alakú utca veszi körül/
Szándékosan cseréltem fel a sorrendet, mert számomra a b) nem egyértelmű. Mi van, ha B egy sarokházban lakik. Vehetem úgy, hogy mindkét utca lakója? Ugyanis szerintem függ ettől a tranzitivitás.
Ja, az első két feladatról: az 1. Egy "Urbán: Matek+" című könyvben találtam,(egyben könyvajánlás; szerintem érdekes feladatokat rejt, egyedi megoldásokal), a második feladat pedig egy régi Arany Dani példa volt.
|
|
| [3] lorantfy | 2003-11-24 23:43:18 |
 Mivel a fiatalok nem nyüzsögnek, beírom az elsőt:
1. feladat megoldása: Legyen „a” pozitív egész szám, összes pozitív osztója: p1,p2,p3,...pn.
A következő tört értékét keressük:
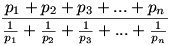
Szorozzuk be a számlálót és nevezőt is a-val.
A nevezőben lévő összeg:
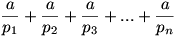
nem más mint „a” pozitív osztóinak összege, hiszen pi azért osztója „a”-nak, mert létezik pj, hogy pipj=a, vagyis  . .
Így a tört értéke: „a” .
(Persze szóban is elintézhettem volna: Ha az osztók reciprokösszegét „a”-val megszorozzuk, az osztók összegét kapjuk. Gyakoroltam kicsit a törtek beírását.)
|
| Előzmény: [1] Suhanc, 2003-11-23 19:04:38 |
|
| [2] lorantfy | 2003-11-23 21:57:19 |
 Kedves Suhanc!
Ügyes a két példa! Nem írom be a megoldást, gondolkodjon más is rajta. (Érdemes különben belenézni a TeX-be – én kimásoltam Word-be, igy folyamatosan lapozható – mert egy négyzetreemelés vagy pl. a törtek nagyon könnyen beírható és sokkal jobban mutat a képlet!)
Egy tényleg villám feladat:
3. Tranzitív egy reláció ha A B és B B és B C C A A C C
Tranzítív-e:
a) az A szomszédja B-nek
b) az A egy utcában lakik B-vel
c) az A barátja B-nek
d) az A testvére B-nek
reláció?
|
|
| [1] Suhanc | 2003-11-23 19:04:38 |
 Sziasztok!
Néha túl fáradt vagyok, hogy egy-egy feladat megoldásába mélyebben elmerüljek, vagy sokáig foglalkozzam vele, és otthagyom. Gondolom, ez ismerős dolog másoknak is. Ezért szerintem jó lenne egy hely, ahova olyan feladatok kerülnek, amelyek megoldása nem igényel 10-15 percnél hosszabb elmélyülést, azonban a megoldás szép, nem darálós fajta. Kezdetnek itt van 2 -valóban ujjgyakorlatni:)-feladat:
1. Egy pozitív egész szám pozitív osztóinak összegét elosztottuk a pozitív osztók reciprokösszegével. Mennyi a hányados?
2. Ha a; b nemnegatív valós számok és c tetszőleges valós szám, bizonyítsd be, hogy:
a+4b+(4c)*(4c)>= 5+4c -1/a -1/b
(bocsi, a képletszerkesztés nem az erősségem)
|
|





 B és B
B és B A
A