|
| [160] Hajba Károly | 2004-05-11 00:29:46 |
 Megoldás László nem is annyira ujjgyakorlat 32. feladatára:
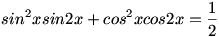
Három ismert trigonometriai egyenlőséget behelyettesítve:
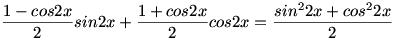
Majd szépen rendezve:
sin2x-sin2xcos2x+cos2x+cos22x=sin22x+cos22x
(sin2x+cos2x)-sin2x(sin2x+cos2x)=0
(sin2x+cos2x)(1-sin2x)=0
 1=67,5°;... 1=67,5°;... 2=157,5°;... 2=157,5°;... 3=45° 3=45°
|
| Előzmény: [109] lorantfy, 2004-02-10 08:18:20 |
|
| [159] BohnerGéza | 2004-05-09 11:13:36 |
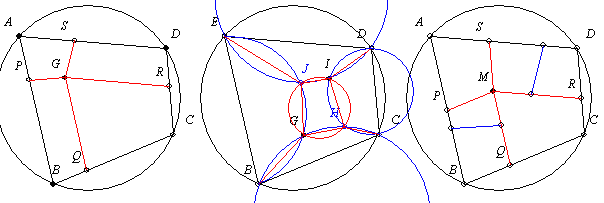
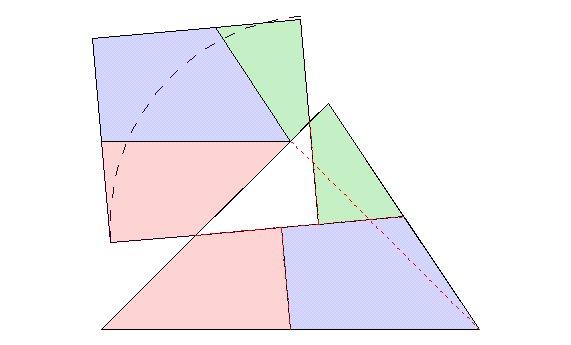
 A 42. feladathoz: (Mutassuk meg, hogy minden húrnégyszög felbontható n>=4 db húrnégyszögre.) A feladat régóta „áll”, ezért az „ujjgyakorlat” részét megírom, lerajzolom. Nem nehéz belátni, ha fel tudjuk bontani a 4-re, 5-re és 6-ra, akkor n>=4 tetszőleges db-ra is.
Az ábrán látható négyszögekről – leírom, hogy kaptam azokat – „ujjgyakorlat” megmutatni, hogy húrnégyszögek. Ami nehezebb, meg kell mutatni, hogy létezik megfelelő G, G és I, illetve M pont.
A nem triviális esetekben van hegyesszöge az ABCD húrnégyszögnek. Jelöljük egy ilyen csúcsát az A-val. ( Ekkor azt hiszem mindig léteznek az alább leírt felbontások esetén a megfelelő pontok. )
A négy részre bontást – ábra első része – úgy kapjuk, hogy megfelelő G-t választunk, majd legyen GR || AD, GQ || AB, valamint PBQB és GRDS húrtrapéz.
Az öt részre bontást – ábra középső része – úgy kapjuk, hogy a G és I pontokat felvesszük megfelelő helyre úgy, hogy a rajtuk és a megfelelő csúcsokon átmenő körök messék egymást még a H illetve J pontban.
Az hat részre bontást – ábra utolsó része – úgy kapjuk, hogy megfelelő M esetén a PBQM és MRDS „elég hosszú” paralelogrammák legyenek, majd azokat két-két húrtrapézra bontjuk.
|
 |
| Előzmény: [135] Csimby, 2004-04-11 22:16:40 |
|
| [158] Hajba Károly | 2004-05-07 12:27:10 |
 Kedves Péter!
Nem nehéz belátni a 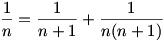 egyenlőséget, s ebből következik, hogy k=2 feltétel is elég. A jobb oldalt tovább lehet bontani és így akármeddig lehet bontogatni. egyenlőséget, s ebből következik, hogy k=2 feltétel is elég. A jobb oldalt tovább lehet bontani és így akármeddig lehet bontogatni.
Üdv: HK
|
| Előzmény: [156] nadorp, 2004-05-07 11:11:48 |
|
| [157] Kós Géza | 2004-05-07 12:09:28 |
 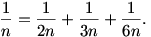
Az általánosabb feladat úgy szól, hogy minden pozitív racionális szám felírható véges sok különböző pozitív egész reciprokösszegeként. Ez ebben a formában nem ujjgyakorlat, de egy kis segítséggel az.
Vegyünk tehát egy pozitív racionális számot. A pozitív egészeket keressük ,,mohón'', azaz mindig a lehető legkisebbet válasszuk ki, ami még nem szerepelt, és a reciprokösszeg nem nő túl nagyra. Például, ha az 1,36 számot szeretnénk felírni, akkor a kiválasztott számok: 1, 3, 38, 2850.
47b feladat: Igazoljuk, hogy a mohó algoritmus mindig eredményre vezet.
|
| Előzmény: [156] nadorp, 2004-05-07 11:11:48 |
|
| [156] nadorp | 2004-05-07 11:11:48 |
 A 47. feladat kapcsán jutott eszembe.
47.a feladat: Bizonyítsuk be, hogy minden 1 nél nagyobb n pozitív egész szám reciproka előállítható k darab (2 k k n2) különböző pozitív egész reciprokának összegeként. n2) különböző pozitív egész reciprokának összegeként.
|
| Előzmény: [146] Hajba Károly, 2004-05-04 12:33:58 |
|
|
|
| [152] lorantfy | 2004-05-05 19:29:18 |
 Kedves Géza és Fórumosok!
Valóban a B-ből induló magasságra nincs szükség, ez volt a félrevezetés, ui. egy "átlagos" hegyesszögű  -ben a talppontja elég közel esik ahhoz az M ponthoz amire négyzetet kapunk. -ben a talppontja elég közel esik ahhoz az M ponthoz amire négyzetet kapunk.
A DF1F2E paralelogramma DF2 átlója egyenlő a RPQT2 téglalap QT2 oldalával. Tehát, ha meg tudnánk szerkeszteni a leendő négyzet x oldalát, akkor F2 pontból kimetszhetnénk vele AC-ből a D pontot. Ezután A pont tükörképe D-re adja az M pontot.
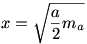 , tehát egyszerű mértani közép szerkesztéssel megkaphatjuk x-t az egyik oldal feléből és a hozzá tartozó magasságból. , tehát egyszerű mértani közép szerkesztéssel megkaphatjuk x-t az egyik oldal feléből és a hozzá tartozó magasságból.
|
 |
| Előzmény: [151] Kós Géza, 2004-05-05 13:55:04 |
|
| [151] Kós Géza | 2004-05-05 13:55:04 |
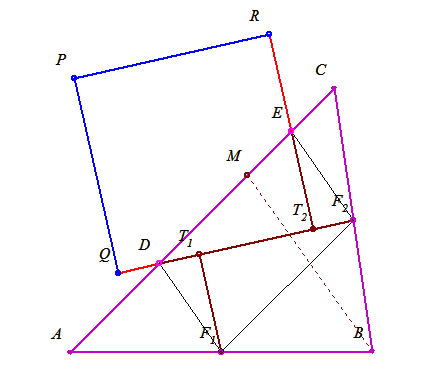
 Ahogy látom, a B-ből induló magasságra nincs is szükség. Az M pont bárhol lehet az AC oldalon, feltéve, hogy a T1 és T2 pontok nem kerülnek a DF2 szakaszon kívülre.
46b. feladat: Szerkesszük meg az AC oldalon azt az M pontot, amire az RPQT2 téglalap négyzet lesz.
|
| Előzmény: [144] lorantfy, 2004-05-02 10:39:46 |
|
|
| [149] Hajba Károly | 2004-05-04 21:38:33 |
 Kedves Géza és László!
Ha most politikus lennék, azt mondanám: Nem is mondtam, hogy négyzet! :o)
Az igazság az, hogy a területegyezőségekben mélyedtem el, s felelőtlen, slendrián kijelentésemet főleg erre értettem, ami persze igaz, de tény, hogy nem vetődött fel bennem a nemnégyzet lehetősége.
Tehát, ha egy ácshajszálnyival is, de nem feltétlenül négyzet, mely a mellékelt ábrából is kitűnik.
HK
|
 |
| Előzmény: [147] Kós Géza, 2004-05-04 12:48:51 |
|
|
|
| [146] Hajba Károly | 2004-05-04 12:33:58 |
 47. feladat:
Létetik-e olyan a N+, melynek reciproka felbontható véges számú különböző prím reciprokösszegére? N+, melynek reciproka felbontható véges számú különböző prím reciprokösszegére?
HK
|
|
|
| [144] lorantfy | 2004-05-02 10:39:46 |
 Kedves Fórumosok!
A következő feladat Bólyai Farkas egy híres átdarabolásából született.
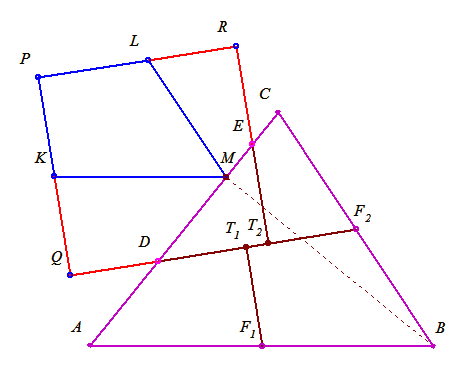
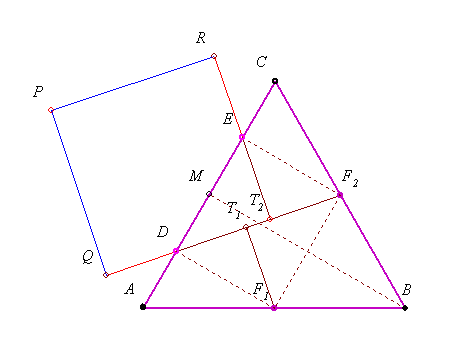
46. feladat: Legyen ABC hegyesszögű  AB oldalának felezőpontja F1, BC oldalának felezőpontja F2 és a B csúcsból induló magasság talppontja M. AB oldalának felezőpontja F1, BC oldalának felezőpontja F2 és a B csúcsból induló magasság talppontja M.
Legyenek AM és MC felezőpontjai D és E. Húzzuk meg a DF2 egyenest és állítsunk rá merőlegest az F1 és E pontokból. Ezek talppontjai legyenek T1 és T2. Tükrözzük a T1 pontot D-re, a T2 pontot E-re. A tükörképek legyenek Q és R. Ezekben a pontokban állított merőlegesek metszéspontja legyen P.
Igyaz-e, hogy a keletkezett négyszög négyzet és területe megegyezik az ABC  területével? területével?
|
 |
|
| [143] lorantfy | 2004-05-02 10:05:37 |
 Kedves Károly!
Ezt a kis feladatot amolyan EU-belépési tesztnek szántam. Gratulálok! Te már beléphetsz!
Rajzos megoldás: a sárgára szinezett részek a kék és piros részt is a terület felére egészíti ki.
|
 |
| Előzmény: [142] Hajba Károly, 2004-05-02 00:26:06 |
|
| [142] Hajba Károly | 2004-05-02 00:26:06 |
 Megoldás a 45. feladatra:
Egy-egy háromszög területe a négyzet területének felével egyenlő, vagyis a két háromszög területe épp a négyzetével egyenlő. (azaz fehér + 2*piros = négyzet) Így amennyi az átfedésük területe (piros), annyinak kell lennie a le nem fedett területnek (kék) is.
Ezt a feladatot annyiban lehet általánosítani, hogy akár téglalapon és bármely két oldalára felvett háromszöggel is igaz.
HK
|
| Előzmény: [141] lorantfy, 2004-05-02 00:04:39 |
|
| [141] lorantfy | 2004-05-02 00:04:39 |
 45. feladat: Egy négyzet két szomszédos oldalán felvettünk egy-egy tetszőlegesen választott pontot, melyet összekötöttünk a szemközti oldal végpontjaival. Igazoljuk, hogy az így keletkezett pirosan színezett síkidom területe megegyezik a kékkel színezett síkidomok területeinek az összegével!
|
 |
|
|
| [139] Csimby | 2004-04-18 16:06:00 |
 43. feladat megoldása:
n=(102k+1-1)/9-2*(10k+1-1)/9=(102k+1-2*10k+1+1)/9=((10k+1-1)/3)2
Mivel 10k+1-1 csupa 9-esből áll, osztható 3-mal, tehát (10k+1-1)/3 egész szám, n pedig négyzetszám!
44. feladat megoldása:
n(n+1)(n+2)(n+3)=6n+11n2+6n3+n4, ugyanakkor 6n+11n2+6n3+n4+1=(n2+3n+1)2
Két négyzetszám különbsége pedig nem lehet 1 (kivéve, ha az egyik a 0, hiszen (n+1)2-n2=2n+1 ami csak n=0-ra egyenlő 1-gyel).
Hasonlít a 43. feladathoz a tanárképző főiskolák idei Péter Rózsa matematika versenyének 1. feladata (legyen ez a 45. feladat):
A=177...76 (2k+3 jegyű), B=355...52 (k+2 jegyű). Biz. be, hogy 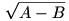 természetes szám és mondjuk meg, hogy hány jegyű. természetes szám és mondjuk meg, hogy hány jegyű.
|
| Előzmény: [138] Suhanc, 2004-04-17 22:00:51 |
|
| [138] Suhanc | 2004-04-17 22:00:51 |
 Kedves Fórumosok!
Az alábbi két feladattal Bonifert Domonkos: Néhány tipikus problémaszituáció matematikából c. könyvében találkoztam.
Szerintem okozhatnak néhány kellemes percet, mégha komoly fejtörést nem is...
43.feladat Lássuk be, hogy n=111...111-222...222
(2k db 1-es, és k db 2-es) minden k>o egészre négyzetszámot ad!
44.feladat Lássuk be, hogy n(n+1)(n+2)(n+3) nem lehet négyzetszám, ha n poz. egész!
|
|
| [137] nadorp | 2004-04-14 08:22:25 |
 Kedves Csimby !
A 41. feladatra inkább ebben a topicban adok egy megoldást, mert a bizonyítás algebrai, bár az ötletet a háromszögbe írható körhöz húzott érintőszakaszok adták.
Legyen a=y+z, b=x+z, c=x+y. Ekkor az egyenlőtlenség az alábbi alakba írható:
(y+z)2.2x+(x+z)2.2y+(x+y)2.2z 3(y+z)(x+z)(x+y) 3(y+z)(x+z)(x+y)
6xyz x2y+xy2+x2z+xz2+y2z+yz2 vagy "szebben" írva x2y+xy2+x2z+xz2+y2z+yz2 vagy "szebben" írva
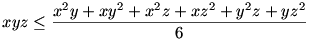
A fenti egyenlőtlenség pedig azonnal következik a számtani és mértani közép közötti összefüggésből.
|
| Előzmény: [134] Csimby, 2004-04-11 22:10:02 |
|
| [136] Csimby | 2004-04-11 22:21:43 |
 A 41. és 42. feladatot a Geometria témába akartam rakni, de most már mindegy...
|
|



 4=225° :o)
4=225° :o) 



 k
k MB.
MB. 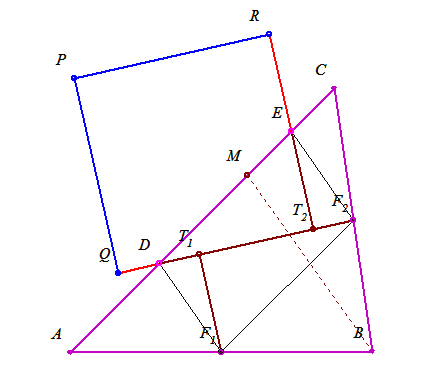

 -ben a talppontja elég közel esik ahhoz az M ponthoz amire négyzetet kapunk.
-ben a talppontja elég közel esik ahhoz az M ponthoz amire négyzetet kapunk. 

 N+, melynek reciproka felbontható véges számú különböző prím reciprokösszegére?
N+, melynek reciproka felbontható véges számú különböző prím reciprokösszegére? 



