| [227] lorantfy | 2004-12-13 10:27:36 |
 63/c. feladat: Legyen A n darab 1-es számjegyből álló 2-es számrsz-beli szám. Mennyi lehet az n értéke ha az n*A 2-es számrsz-beli szám számjegyeinek összege éppen n.
|
|
|
| [225] Csimby | 2004-12-13 00:16:29 |
 Húú, de nagy baromságot írtam az előbb... Asszem ilyen alakú lesz az eredmény:
1111101001111...1111000001011
És középen 1994 db. 1-es van, tehát a számjegyek összege: 1994+9 = 2003, de lehet, hogy elszámoltam...
|
| Előzmény: [224] Csimby, 2004-12-13 00:03:18 |
|
|
| [223] lorantfy | 2004-12-12 22:22:56 |
 Kedves Károly!
Ha jól számolom, akkor a számjegyek összege: 2004*6=12024.
63/b feladat: Mi a helyzet, ha A-t 2-es számrendszerbeli számnak tekintjük? Mennyi lesz a 2004*A 2-es számrsz-beli szám számjegyeinek öszege?
|
| Előzmény: [222] Hajba Károly, 2004-12-08 23:34:22 |
|
| [222] Hajba Károly | 2004-12-08 23:34:22 |
 63. feladat:
Legyen A=111...<2004 db>...111. Mennyi a 2004*A szorzat számjegyeinek összege?
(Ambrózy Géza emlékverseny V-VI. o. feladat alapján)
HK
|
|
| [221] lorantfy | 2004-12-06 14:23:00 |
 Kedves Attila!
Szép a megoldásod! Kedves olvasók, érdemes ezeket a trükköket begyakorolni!
A triv. megoldást leválasztva én így alakítottam:
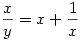
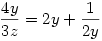
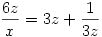
Összeszorozva az egyenleteket a bal oldal értéke 8. Ez csak úgy lehet ha x=2y=3z=1 és a megoldások kielégítik az eredeti egy.rsz-t.
|
| Előzmény: [220] jenei.attila, 2004-12-06 13:26:28 |
|
| [220] jenei.attila | 2004-12-06 13:26:28 |
 Az előző hozzászólásomban a helyettesítés bevezetése fölösleges, talán csak egy kicsit áttekinthetőbb így. Elmaradt anna ellenőrzése, hogy a kapott értékek tényleg megoldást adnak, hiszen összeadás után csak azt kapjuk, hogy ha egyáltalán van megoldás, akkor az csak ez lehet. Ez behelyettesítéssel könnyen ellenőrizhető.
|
| Előzmény: [219] jenei.attila, 2004-12-06 13:02:07 |
|
| [219] jenei.attila | 2004-12-06 13:02:07 |
 Az előző egyenletnél, ha egyik ismeretlen sem 0, akkor vezessük be az a=1/x, b=1/y, c=1/z helyettesítést. Mindegyik egyenletet osszuk el a jobb oldalával, és az új helyettesítést felhasználva a b-a2=1,2/3c-1/4b2=1,2a-1/9c2=1 egyenleteket kapjuk. Ezeket összeadva, (a-1)2+(b/2-1)2+(c/3-1)2=0 adódik. Innen x=1, y=1/2, z=1/3. Természetesen az x=y=z=0 is megoldás.
|
| Előzmény: [218] lorantfy, 2004-12-06 11:47:51 |
|
|
| [217] Hajba Károly | 2004-12-06 08:44:01 |
 Megoldás a 62. feladatra:
(1)...x2+xy+y2
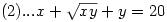
------------------
(1)...(x+y)2-xy=200
(2)...xy=(20+x+y)2
------------------
(1-2)...(x+y)2-(20+x+y)2=200
20(2x+2y-20)=200
x+y=15 ill. xy=25 innen:
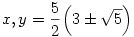
HK
|
| Előzmény: [216] lorantfy, 2004-12-05 09:56:51 |
|
| [216] lorantfy | 2004-12-05 09:56:51 |
 Az előző egyenletrendszernek nem volt nagy sikere. Ez most jóval könnyebb:
62. feladat:
x2+xy+y2=200
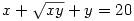
|
|
|
|
| [213] lorantfy | 2004-11-28 11:12:05 |
 Kedves Lajos!
Nekem egy valós számhármas jött ki (1,1/2,1/3) és úgy látszik nem is lehet több. Azért mertem az ujjgyakorlatok közé tenni, mert 2-3 húzással nagyon trivi formára lehet hozni.
|
| Előzmény: [212] Lóczi Lajos, 2004-11-28 02:02:58 |
|
| [212] Lóczi Lajos | 2004-11-28 02:02:58 |
 Érdekes feladat, 2 valós megoldást (számhármast) találtam, de emellett 6 komplex számhármast is, amelyek kissé bonyolult (egyváltozós) hatodfokú egyenletek megoldásaiból jönnek. Ugye nem ezekre gondoltál? :)
|
| Előzmény: [211] lorantfy, 2004-11-27 20:59:39 |
|
| [211] lorantfy | 2004-11-27 20:59:39 |
 61. feladat: Oldjátok meg az alábbi egyenletredszert:
x2-y = x2y
8y2-3z = 12y2z
18z2-x = 9z2x
|
|
| [210] lorantfy | 2004-11-18 09:12:44 |
 60. feladat megoldása: Könnyű belátni, hogy
(a,b).[a,b]=a.b
hiszen a lkkt-t pont úgy kapjuk, hogy a két szám szorzatából kihagyjuk a közös prímtényezőket. Ezek szorzata meg pont a lnko. Így aztán a.b=b.c=a.c amiből a=b=c.
|
| Előzmény: [208] Gubbubu, 2004-11-17 22:38:15 |
|
| [209] Gubbubu | 2004-11-17 22:55:33 |
 Hát, egyelőre nemigen tudok rájönni. Sajnos, az eredeti papíromat talán egy hónapja is, hogy kidobtam, és nagyon kevés az időm, hogy újra rekonstruálni próbáljam. Na mindegy, ha valaki ki tudja valahogy javítani, csak nyugodtan, ha meg nem, hagyjuk a fenébe.
|
| Előzmény: [207] Gubbubu, 2004-11-17 22:29:37 |
|
| [208] Gubbubu | 2004-11-17 22:38:15 |
 Addig is egy új szellemes kis feladat, amiből (többek közt) ma zéháztam: 60. feladat Az a,b,c>0 egész számokra teljesül
(a,b)=(b,c)=(c,a)
és
[a,b]=[b,c]=[c,a]
.
(azaz lnko-ik és lkkt-ik páronként egyenlőek).
Igazoljuk, hogy a=b=c !
|
|
|
| [206] Gubbubu | 2004-11-17 22:28:33 |
 Igen, az a trükk, hogy a szélső tényezőket kell egymással szorozni (az elsőt a hatodikkal, a másodikat az ötödikkel, a harmadikat a negyedikkel), ekkor szinte azonos másodfokú polinomok szorzatát kapjuk, ami új változó bevezetésével szép harmadfokú egyenletté redukálható - mely utóbbit pl. "racionális gyökteszttel" lehet megoldani megfelelő n-ekre.
Köszönöm a megoldásokat.
|
| Előzmény: [198] lorantfy, 2004-11-09 09:30:55 |
|
| [205] lorantfy | 2004-11-10 23:30:04 |
 Kedves Károly!
Ügyes kis példa, de egy prímszám tábla nem árt hozzá: itt
59. feladat megoldása: A bal oldalból (p-q) kiemelhető, a 83805 minden osztója páratlan. Két prímszám különbsége csak akkor lehet páratlan, ha egyik 2.
Tehát q=2. Ezt visszaírva:
p(1+p+p3)=83827=17.4931
Ebből p=17 és 1+p+p3 pont 4931 lesz.
|
| Előzmény: [202] Hajba Károly, 2004-11-10 08:10:13 |
|
| [204] nadorp | 2004-11-10 13:31:48 |
 Kedves Gubbubu !
Az 56. példát valahogy nem értem, mert nem igaz pld szabályos háromszögre, ui. legyen a=b=c. Ekkor szerinted
 , ami nyilván nem igaz minden a-ra. , ami nyilván nem igaz minden a-ra.
|
| Előzmény: [191] Gubbubu, 2004-10-08 09:48:03 |
|
|







