| [252] jonas | 2005-03-21 21:46:47 |
 Nos, 64 számjeggyel fel lehet írni őket:
1001000010101011001011011010000011001110011000011101010011110010\ 011011111110100101000110101111011000100010111011100011111000000
Azonban ez 127 számjegy, ezért nem valószínű, hogy egy fiú egy sorba fel tudja írni őket (ha több sorba írja, akkor már meg kell ismételni legalább egy 1-est). Itt a fórumon sem fért el egy sorban, ezért meg kellett törnöm. Én tehát arra szavazok, hogy Jancsi ugrat minket, valójában Juliska írta a számsort.
Lehet, hogy ennél kevesebb számjeggyel is meg lehet csinálni, nem tudom.
|
| Előzmény: [250] lorantfy, 2005-03-18 00:13:13 |
|
| [251] levi | 2005-03-21 17:22:28 |
 Sejtés a 67.b feladatra: Ha veszünk egy n számjegyű számot (csupa 0-ból és 1-ből, akkor a keresett "láncban" mindig 2n-1 darab 1-es lesz (és ekkor 2n-1-1 db 0).
n=2 esetén variációk: 11,10 a lánc:110 és 2n-1=2, azaz itt müködik
n=3 esetén variációk: 111, 110, 101, 100 a lánc: 1110100 és 2n-1=4, azaz itt is működik
n=4-re is megnéztem, azt most nem írom le, tehát ha a sejtés igaz, akkor n=7 esetén 2n-1=64 lesz. Azaz elvileg Jancsi igazat mondott.
|
| Előzmény: [250] lorantfy, 2005-03-18 00:13:13 |
|
| [250] lorantfy | 2005-03-18 00:13:13 |
 Arra gondoltam csavarként, hogy írhatja folyamatosan egymás után a számjegyeket és bármely egymás után következő hét számjegy lehet egy új 7-jegyű szám, ha 1-es áll az elején.
67.b feladat: Jancsi azt állítja, hogy sikerült felírnia az összes 7 jegyű 1 és 0 számjegyből álló számot 64 db 1-es felhasználásával? Igaza van-e Jancsinak?
|
| Előzmény: [249] Csimby, 2005-03-17 16:20:45 |
|
|
| [248] lorantfy | 2005-03-17 13:44:39 |
 Az első számjegy csak 1-es lehet a további 6 helyiértéken pedig 0 vagy 1, tehát kétféle számjegy állhat. Így 26=64 db ilyen szám van. Írjuk egymás alá ezeket a számokat. Az első oszlopban 64 db 1-es van a többi oszlopban pedig a számjegyek fele 1-es fele 0. Így 64+6*32=256-szor kellett Jancsinak leírnia az 1-es számjegyet.( Feltéve persze, hogy nincs valami trükk a felírásban, ami Csimbytől azért elvárható! )
|
| Előzmény: [247] Csimby, 2005-03-16 23:17:14 |
|
| [247] Csimby | 2005-03-16 23:17:14 |
 67.feladat Jancsi felírta az összes olyan hétjegyű egész számot, amely csak 0 és 1 számjegyeket tartalmaz. Hányszor írta le az 1-es számjegyet?
|
|
|
| [245] Kalmár-Nagy József | 2005-03-01 13:16:32 |
 Ha a-1,a,a+1 köbeit vesszük és rendezzük, elegánsabban kijön. Átalakítások után azt kapjuk, hogy a2(a-6)=2. (az a után a 2 a négyzetet jelölné, csak még lusta voltam a TeX-et megtanulni :) A szorzat mindét tagja egész, mert 'a' is az. Az egyes eseteket gyorsan végig lehet futni.
|
|
| [244] Csimby | 2005-02-28 23:36:21 |
 Suhanc egyenletét és a kongruencia szabályait felhasználva:
Ha a 0 maradékot ad 4-gyel osztva, akkor a bal oldal osztható 4-gyel, a jobb oldal 3 maradékot ad 4-gyel osztva.
Ha a 1 maradékot ad 4-gyel osztva, akkor a bal oldal 1 maradékot, a jobb oldal 3 maradékot ad 4-gyel osztva.
Ha a 2 maradékot ad 4-gyel osztva, akkor a bal oldal osztható 4-gyel, a jobb oldal 1 maradékot ad 4-gyel osztva.
Ha a 3 maradékot ad 4-gyel osztva, akkor a bal oldal 3 maradékot, a jobb oldal 1 maradékot ad 4-gyel osztva.
Mind a 4 esetben ellentmondásra jutottunk, tehát nincsen olyan a amely eleget tenne a feltételeknek.
|
| Előzmény: [242] Suhanc, 2005-02-28 21:00:37 |
|
| [243] Atosz | 2005-02-28 22:00:32 |
 Kedves László és Suhanc!
Nem tudom, hogy mennyire elegáns vagy nem, de a nagy Fermat sejtés (illetve ma már tétel) nem elég erre? Azaz az xn+yn=zn-nek n>2 esetén nincs megoldása.
|
| Előzmény: [241] lorantfy, 2005-02-27 15:38:28 |
|
| [242] Suhanc | 2005-02-28 21:00:37 |
 Kedves László!
Egy nem túl elegáns megodásom lenne a feladatodra:
Legyen a három egymást követő köbszám a3,(a+1)3és(a+2)3 ! Adjunk felső korlátot a értékére, majd a maradék eseteket megvizsgáljuk a végén. A feladat állítása szerint (rendezve az egyenletet):
a3=3a2+9a+7
Bonsuk a3-t három egyenlő részre, mert a jobb oldalon három tag van. Nyilván, ha

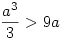
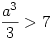
feltételek egyszerre teljesülnek, az egyenletnek nem lehet megoldása, hisz a bal oldal határozottan nagyobb. A három egyenlőtlenség közül az első a legenyhébb, ezért a>9 esetén biztosan nincs megoldás.
Maradt tehát 10 esetünk 0-tól 9 ig. Ezeket behelyettesítve az egynletbe nem kapunk kielégítő megoldást, ezzel a feladat állítását bizonyítottuk.
|
| Előzmény: [241] lorantfy, 2005-02-27 15:38:28 |
|
| [241] lorantfy | 2005-02-27 15:38:28 |
 66. feladat: Bbh. három egymást követő természetes szám közül a legnagyobb köbe nem lehet egyenlő a másik kettő köbének összegével.
|
|
|
| [239] Suhanc | 2005-01-08 08:56:51 |
 Az 55.Feladat szemmel láthatólag nem hozott lázba senkit...;)
Ha esetleg valaki mégis lenne olyan "elvetemült", egy kis segítség:
Ez egy olyan "közepes" feladat...
|
|
| [238] Suhanc | 2005-01-08 08:52:43 |
 Kedves Mindenki!
Ez egy olyan apró gondolat... de szép!:)
65.Feladat:
Igazoljuk, hogy :
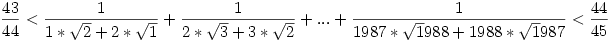
|
|
| [237] lorantfy | 2004-12-21 00:27:58 |
 Páros n-re is igaz lesz, mert ekkor k>n és n végén k-n db 0 áll.
Ekkor viszont (2k-1-n) végén k-n db 1-es fog állni előttük (balra) 0 áll. Így +1 hozzáadása (k-n) db 1-esből 1 db 1-est csinál. A változás -(k-n)+1 a számjegyek összegében.
A számjegyek összege: (m-1)+(k-m)-(k-n)+1=n.
|
| Előzmény: [236] lorantfy, 2004-12-21 00:02:58 |
|
| [236] lorantfy | 2004-12-21 00:02:58 |
 Hello Jónás!
Úgy látszik igazad van, mindketten elszámoltuk Csimbivel: n=200410=111110101002
A számjegyek összege: m=7. Mivel 2 db 0-ra végződik k=2006 lesz. Az első részösszegben m-1=6db 1-es marad. 22006-1-n részben k-m=1999 db 1-es van és ..011-re végződik, így a +1 hozzáadása 1-el csökkenti az 1-esek számát: 6+1999-1=2004.
Ami persze nem jelenti azt, hogy minden n-re igaz.
Páratlan n esetén azonban mindig igaz lesz, mert ilyenkor n 1-re végződik. k=n és 2n-1-n pedig 0-ra végződik, így a +1 a végén 1-el növelei a számjegyek összegét. m-1+k-m+1=k=n.
|
| Előzmény: [235] jonas, 2004-12-20 23:20:48 |
|
| [235] jonas | 2004-12-20 23:20:48 |
 Erdekes, nekem 2004 jon ki.
2004*(22004-1)=111110100111111111111111...1111111111100000101100
Az eredmeny osszesen 2015 szamjegybol all, ebbol 11 nullas es 2004 egyes.
|
| Előzmény: [234] lorantfy, 2004-12-20 22:58:40 |
|
| [234] lorantfy | 2004-12-20 22:58:40 |
 Kedves Suhanc!
Örülök, hogy foglalkoztál a témával. Már azt gondoltam feledésbe merül. (Persze azt nem hagytam volna!)
Szóval az első pár számra én is kipróbáltam és működik amit mondtál. De valahol elromlik, mert annyira szerettem volna, hogy 2004-nél a számjegyek összege 2004 legyen, hogy kétszer is átszámoltam és úgyis csak 2003 lett és Csimbinek is ez jött ki. Tehát 2004-nél már nem igaz!
Én maradtam 2-es számrendszerben. Lenyen n számjegyeinek összege m.
n.(2n-1)=n.2n-n
n.2n legalább n db 0-ra végződő szám. Legyen jobbról az első 1-es a k+1-edik helyiértéken.n k Ekkor k Ekkor
n.2n-n=(n.2n-2k)+(2k-n)=(n.2n-2k)+(2k-1-n)+1
Az összeg első részében a számjegyek összege m-1 és ez független a többitől. 2k-1 k db 1-esből álló szám. Ha ebből elvesszük n-t, a kivonás m darab 0-t hoz létre, így a számjegyek összege a második részben k-m. Sajnos ez változhat még ha az 1-et a végén hozzáadjuk.
Ha nem változik, mert pl. n 0-ra végződik (k>n) akkor a számjegyek összege: m-1+k-m+1=k.
n=k esetén n pont 1-esre végződik, így az 1-es hozzáadása változtathat a második részösszeg számjegyeinek összegén.
Ha ez idáig jó, akkor nem vagyunk messze a megoldástól!
|
| Előzmény: [233] Suhanc, 2004-12-20 18:05:07 |
|
| [233] Suhanc | 2004-12-20 18:05:07 |
 Kedves László!
A feladatötlet nagyon érdekes...:)
Átírtam 10-es számrendszerbe, amiben az állítás: Milyen n-re lesz a (2n-1)*n felbontható n db különböző kettőhatvány összegeként?
megnéztem az első néhány n-re:
(21-1)*1=20
(22-1)*2=22+21
(23-1)*3=24+22+20
(24-1)*4=25+24+23+22
(25-1)*5=27+24+23+21+20
(26-1)*6=28+26+25+24+23+21 (remélem, nem számoltam el..;D)
Azt sejtem, hogy ez minden n-re igaz lesz, de eddig nem találtam olyan indukciót vagy rekurziót, ami ezt megmutatná. Szóval idáig nem sok..;) De hátha ez inspirál valakit a megoldás elkezdéséhez...
|
| Előzmény: [227] lorantfy, 2004-12-13 10:27:36 |
|
| [232] Hajba Károly | 2004-12-15 14:07:07 |
 Kedves Sirpi!
Ez a kérdés szó szerint így hangzott el anno 1982-ben feleségem felvételijén a Közgázon, s ezért jeleztem, hogy beugrató. S a helyes válasz az volt, hogy nem létezik ilyen számrendszer. Ő kicsit leizzadva, kicsit lefehéredve, de odabökte, hogy nincs is ilyen, s elfogadták/felvették. :o)
HK
|
| Előzmény: [231] Sirpi, 2004-12-15 11:15:59 |
|
| [231] Sirpi | 2004-12-15 11:15:59 |
 Nem 2-es számrendszert akartál írni? Az 1/2-essel gondjaim vannak, mert az "egykettedesvessző" előtt végtelen sok számjegyre lenne szükségem.
2-es számrendszerben 1/3 = 0,010101..., mértani sor összegképletével könnyen ellenőrizhető.
1/2-esben (feltéve, hogy csak 0 és 1 használható számjegyként), 1/3 = ...1010100, ami ugye "végtelen hosszú" szám.
|
| Előzmény: [230] Hajba Károly, 2004-12-15 09:36:34 |
|
|
| [229] Hajba Károly | 2004-12-13 22:31:40 |
 Már ha a számrendszereknél tartunk.
64. feladat:
Írjuk fel az 1/2-edes számrendszerben az 1/3-adot!
|
|
|









 k Ekkor
k Ekkor 
