| [26] nadorp | 2003-12-05 09:11:23 |
 Kedves Péter!
Megoldás a 8. feladatra (remélem nem számoltam el)
f(x)=x2n(x+1)2+2x2n-2(x+1)2+3x2n-4(x+1)2+...+n(x+1)2+n+1=(x+1)2g(x)+n+1
Mivel g(x)>0, ezért f(x)>=n+1, egyenlőség n=-1 esetén van
|
| Előzmény: [23] Pach Péter Pál, 2003-12-04 22:24:55 |
|
| [25] lorantfy | 2003-12-04 22:36:37 |
 Kedves Suhanc!
Kösz a megoldást! Ez neked tényleg csak ujjgyakorlat volt.
7.b feladat: Mely egész x,y,z számokra teljesül:
8x2+3y2+6z2+7xy+5yz+x(4+z)+z(4+x)+4=0
Kis nehezítés – Próbálkozzon más is!
(Egy OKTV feladat alapján)
|
| Előzmény: [22] Suhanc, 2003-12-04 21:40:43 |
|
| [24] Pach Péter Pál | 2003-12-04 22:29:34 |
 Igazad van, így tényleg egyszerűbb. :-) De lehet, hogy ha a kilencedikesek a szögfüggvényeket sem ismerik, akkor még a Cauchy-Schwarz-Bunyakovszkij egyenlőtlenséggel sem volt dolguk. :-)
Persze át lehet írni olyan formára, ahol csak azt használjuk, hogy 0 x2, de így a CSB-egyenlőtlenségnek éppen azt a tulajdonságát veszítjük el, ami alapján könnyen észre lehet venni a megoldást. x2, de így a CSB-egyenlőtlenségnek éppen azt a tulajdonságát veszítjük el, ami alapján könnyen észre lehet venni a megoldást.
Maga a megoldás természetesen gyors és korrekt. :-)
|
| Előzmény: [19] Kós Géza, 2003-12-04 14:11:14 |
|
| [23] Pach Péter Pál | 2003-12-04 22:24:55 |
 Kedves László!
A körülírás alapján azt hittem, hogy az 1993./3. feladatról van szó.
8. feladat
Legyen n adott pozitív egész szám. Határozzuk meg a valós számokon értelmezett
f(x)=x2n+2x2n-1+3x2n-2+…+(2n+1-k)xk+…+2nx+2n+1
polinom minimumát.
|
| Előzmény: [20] lorantfy, 2003-12-04 15:45:19 |
|
| [22] Suhanc | 2003-12-04 21:40:43 |
 A teljes négyzetek:
(a-b/2)2+(c-1)2+3/4*(b-2)2<=0
Nyilván c=1, b=2 a=1
|
|
| [21] lorantfy | 2003-12-04 20:15:31 |
 7. feladat:
Mely egész a, b, c, számokra igaz:
a2+b2+c2+4 ab+3b+2c ab+3b+2c
(1965. évi Kürschák példa alapján)
|
|
| [20] lorantfy | 2003-12-04 15:45:19 |
 Az 5. feladatnál: Ha valaki persze nem akar nagyon trükközni, emelje csak négyzetre mindkét oldalt (ha a bal oldal negatív az egyenlőtlenség úgyis igaz) és alakítsa teljes négyzetté:
9x2+24xy+16y2 25x2+25y2 25x2+25y2
0 16x2-24xy+9y2 16x2-24xy+9y2
0 (4x-3y)2 (4x-3y)2
Láttam én már olyan Kürschák feladatot, ahol a megoldáshoz semmi más nem kellett csak ügyesen teljes négyzetekké alakítani.(Előkeresem!)
|
| Előzmény: [17] nadorp, 2003-12-04 13:36:32 |
|
| [19] Kós Géza | 2003-12-04 14:11:14 |
 Lényegében ugyanaz, de talán kicsit egyszerűbb megtalálni a megoldást Cauchy-Schwarz-Bunyakovszkij egyenlőtlenséggel:
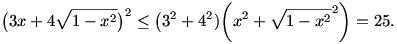
Egyenlőség akkor áll, ha 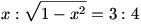 . .
Azzal maximálisan egyetértek, hogy az ilyen trükköket hasznos megtanulni és begyakorolni.
|
| Előzmény: [14] Pach Péter Pál, 2003-12-04 11:06:48 |
|
| [18] lorantfy | 2003-12-04 14:09:36 |
 Kedves Nádor P.!
Nagyon gyors voltál és persze nagyon ügyes!
Most aztán megoldásod alapján rögtön általánosíthatjuk is a feladatot:
6.feladat:
Legyenek a,b,c egy derékszögű háromszög oldalai.
Bbh. 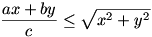 . .
(Más módszerrel oldjuk meg!)
|
| Előzmény: [17] nadorp, 2003-12-04 13:36:32 |
|
| [17] nadorp | 2003-12-04 13:36:32 |
 Megoldás az 5. feladatra.
Legyenek p és q pozitív egész számok, melyek értékét majd később adjuk meg. Ekkor a számtani és a négyzetes közép közötti összefüggés miatt
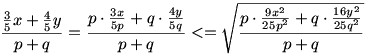
Ebből
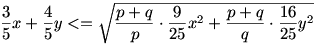
Látszik, hogy a p=9 q=16 választással épp a kívánt egynelőtlenséget kapjuk.
|
| Előzmény: [15] lorantfy, 2003-12-04 13:01:55 |
|
| [16] Hajba Károly | 2003-12-04 13:25:06 |
 Kedves László!
Én a geometria oldaláról közelítve találtam egy "csűrcsavarta" megoldást.
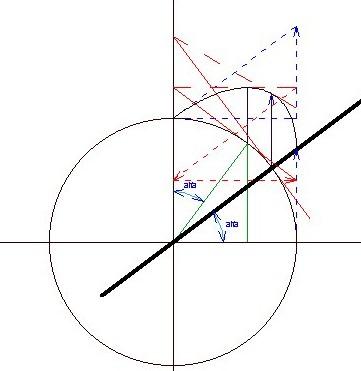
A maximumhely X koordinátájának keresésekor nem számít, ha az egész függvényt elosztom 4-gyel. Így egy origón átmenő, 0,75 meredekségű egyenes és origó központú egység sugarú kör összegét kapjuk.
Torzítsuk el képzeletben a körív minden pontját úgy, hogy az egyenes és X tengely közötti távolsággal távolítsuk az X tengelytől el. Ez a függvény képe és egyben egy ellipszis is. Szerkesszük meg a kőr és a hozzá tartozó ellipszis pontokhoz illesztett, összetartozó érintőket. Ezen érintők az Y tengelyen metszik egymást, mivel ott az eltolás 0. Az ellipszis maximumhelyéhez tartozó érintő párhuzamos az X tengellyel. Könnyen belátható, hogy e két érintő által bezárt szög  , így a kör ezen érintőpontját az eredeti egyenes y=x tengelyre történő tükrözött egyenessel képzett metszéspont adja. , így a kör ezen érintőpontját az eredeti egyenes y=x tengelyre történő tükrözött egyenessel képzett metszéspont adja.
Ezt visszatéve a függvényekre, a megoldást a kör és az egyenes inverzének metszéspontja adja.
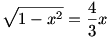
Ennek eredménye éppen 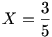
HK
|
 |
| Előzmény: [11] lorantfy, 2003-12-03 18:28:14 |
|
| [15] lorantfy | 2003-12-04 13:01:55 |
 Na ez már igen!
Kedves Péter!
Köszönöm a megoldást!
Érdemes a "közepek" közötti összefüggéseket jól begyakorolni, mert versenyfeladatoknál és néha-néha még KÖMAL feladatokban is nagy hasznát vehetjük!
Akkor próbálkozzatok ezzel:
5.feladat Bbh. 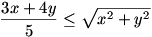
|
| Előzmény: [14] Pach Péter Pál, 2003-12-04 11:06:48 |
|
| [14] Pach Péter Pál | 2003-12-04 11:06:48 |
 Megoldás a 4. feladatra
Írjuk fel a számtani és a négyzetes közepek közti egyenlőtlenséget 9 darab 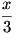 -ra és 16 darab -ra és 16 darab  -re: -re:
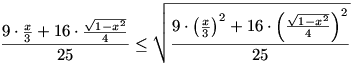
Mindkét oldalt egyszerűbb alakra hozva:
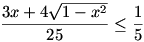
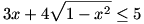
Így a kifejezés maximuma 5, amit pontosan akkor vesz fel, ha 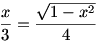 , azaz, ha , azaz, ha 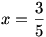 . .
|
| Előzmény: [11] lorantfy, 2003-12-03 18:28:14 |
|
| [13] lorantfy | 2003-12-04 00:16:58 |
 Kedves Attila!
Szép a megoldás. Köszönet érte!
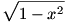 -ből adja magát ez a helyettesítés, de sajnos a 9-edikesek még nem tanulták matekból a szögfgv-ket. Kérdés a tankönyvírók hogy gondolták a megoldást? Hátha valakinek van még más ötlete. -ből adja magát ez a helyettesítés, de sajnos a 9-edikesek még nem tanulták matekból a szögfgv-ket. Kérdés a tankönyvírók hogy gondolták a megoldást? Hátha valakinek van még más ötlete.
|
| Előzmény: [12] evilcman, 2003-12-03 22:47:58 |
|
| [12] evilcman | 2003-12-03 22:47:58 |
 4. megoldás:
kikötés: 1>=x>=-1
ha ez az intervallum, akkor x-et helyettesíthetjük sin ( ) -val ) -val
így-ha A a maximuma a függvénynek:
A=3sin ( )+4cos ( )+4cos ( ) )
elosztjuk mindket oldalt 5-tel

legyen 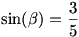 ezért ezért 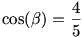
így addíciós képlettel:

a sinus függvénynek a maximuma 1, vagyis az eredeti függvény maximuma 5
Innen pedig már ki lehet számolni x-et, az eredeti egyenlet egyetlen gyöke 3/5.
|
|
| [11] lorantfy | 2003-12-03 18:28:14 |
 4.feladat: Keressük a maximum helyét és értékét, de semmi deriválás, kilencedikesek vagyunk!
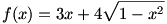
(Sokszínű Matek 9-ből van!)
|
|
|
| [9] lorantfy | 2003-12-02 14:11:11 |
 Kedves Fórumosok!
Nézzetek be ide is mert kihal a téma!
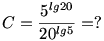
|
|
| [8] Suhanc | 2003-11-27 18:03:42 |
 Igen, tényleg elírtam! Nem szerencsés:(
|
|
| [7] lorantfy | 2003-11-26 22:04:42 |
 Kedves Suhanc!
Szépen elvagyunk itt ketten ebben a témában. Beírok egy megoldást - de szerintem elírtad a 4c2-et!
2. feladat megoldása: Belátjuk, hogy
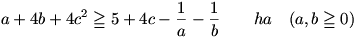
A 4c2-ből és a 4c-ből látszik, hogy bal oldalon egy különbség négyzete lesz, amihez kell még, hogy mindkét oldalhoz 1-et adjunk:
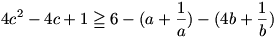
Jobb oldalon a jól ismert egyenlőtlenség:
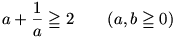
és a második tag is ilyen lesz, ha kiemelünk 2-t:

|
| Előzmény: [1] Suhanc, 2003-11-23 19:04:38 |
|
| [6] Suhanc | 2003-11-26 18:24:56 |
 Hahó!
Szakkörön kaptunk két érdekes feladatot, a témakört nem árulom el, elég könnyen kiderül. Az egyik tényleg villámkérdés, a másikról a szakkörvezető ennyit mondott: "aki ismeri a trükköt, annak trivi, aki még nem, annak lesz min gondolkodnia" :)
4. Bizonyítsuk be, hogy tekintve 2 ; 3; és 5 n. hatványainak összegét, van olyan két szám, melyek különbsége osztható 1237-tel. (ígérem, nemsokára megtanulom a képletszerkesztést)
5. Tekintsünk 512 egész számot! Bizonyítsuk be, hogy ki tudunk választani közülük néhányat, hogy összegük 512-vel osztható legyen! (leglább 1-et választunk ki, de akár az összeset is)
|
|
| [5] lorantfy | 2003-11-26 14:57:05 |
 Kedves Suhanc!
Jól gondolod, pont a sarokház az ellenpélda a b)-nél.
A d)-nél szigorú értelemben igazad van. De ha azt mondjuk, hogy testvérek azok, akiknek legalább egyik szülője közös, akkor már nem.
Szóval tágabb értelemben egyik sem tranzitív.
|
| Előzmény: [4] Suhanc, 2003-11-25 20:16:51 |
|
| [4] Suhanc | 2003-11-25 20:16:51 |
 Kedves Lórántfy!
Ha valóban ennyire "nagy" az érdeklődés, akkor én is leírom a 3. feladatra az ötleteimet.
d)nyilván tranzitív. c) Nem tranzitív./sajnos a suli számos ellenpéldát hoz a tranzitivitásra :( /
a) ha A és B szomszédok, valamint B és C szomszédok, úgy A és C B két oldalán laknak, így nem lehetnek szomszédok (eltekintve egy olyan speciális elhelyezéstől, amelyben a 3 házat egy kör alakú utca veszi körül/
Szándékosan cseréltem fel a sorrendet, mert számomra a b) nem egyértelmű. Mi van, ha B egy sarokházban lakik. Vehetem úgy, hogy mindkét utca lakója? Ugyanis szerintem függ ettől a tranzitivitás.
Ja, az első két feladatról: az 1. Egy "Urbán: Matek+" című könyvben találtam,(egyben könyvajánlás; szerintem érdekes feladatokat rejt, egyedi megoldásokal), a második feladat pedig egy régi Arany Dani példa volt.
|
|
| [3] lorantfy | 2003-11-24 23:43:18 |
 Mivel a fiatalok nem nyüzsögnek, beírom az elsőt:
1. feladat megoldása: Legyen „a” pozitív egész szám, összes pozitív osztója: p1,p2,p3,...pn.
A következő tört értékét keressük:
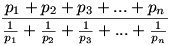
Szorozzuk be a számlálót és nevezőt is a-val.
A nevezőben lévő összeg:
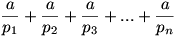
nem más mint „a” pozitív osztóinak összege, hiszen pi azért osztója „a”-nak, mert létezik pj, hogy pipj=a, vagyis  . .
Így a tört értéke: „a” .
(Persze szóban is elintézhettem volna: Ha az osztók reciprokösszegét „a”-val megszorozzuk, az osztók összegét kapjuk. Gyakoroltam kicsit a törtek beírását.)
|
| Előzmény: [1] Suhanc, 2003-11-23 19:04:38 |
|
| [2] lorantfy | 2003-11-23 21:57:19 |
 Kedves Suhanc!
Ügyes a két példa! Nem írom be a megoldást, gondolkodjon más is rajta. (Érdemes különben belenézni a TeX-be – én kimásoltam Word-be, igy folyamatosan lapozható – mert egy négyzetreemelés vagy pl. a törtek nagyon könnyen beírható és sokkal jobban mutat a képlet!)
Egy tényleg villám feladat:
3. Tranzitív egy reláció ha A B és B B és B C C A A C C
Tranzítív-e:
a) az A szomszédja B-nek
b) az A egy utcában lakik B-vel
c) az A barátja B-nek
d) az A testvére B-nek
reláció?
|
|





 x2, de így a CSB-egyenlőtlenségnek éppen azt a tulajdonságát veszítjük el, ami alapján könnyen észre lehet venni a megoldást.
x2, de így a CSB-egyenlőtlenségnek éppen azt a tulajdonságát veszítjük el, ami alapján könnyen észre lehet venni a megoldást. 


 , így a kör ezen érintőpontját az eredeti egyenes y=x tengelyre történő tükrözött egyenessel képzett metszéspont adja.
, így a kör ezen érintőpontját az eredeti egyenes y=x tengelyre történő tükrözött egyenessel képzett metszéspont adja. 

 B és B
B és B A
A