| [261] lorantfy | 2005-03-26 01:09:14 |
 Ez jól van így. Majdnem olyan, mint ahogy a nagykönyvekben meg van írva. Még egy +C-t szoktak hozzáírni, minthogy ez határozatlan integrál, szóval egy konstans erejéig határozatlan. Ha visszaderiválsz a konstans eltűnik, így bármi lehet.
Arra a kérdésre, mi van, ha a kerek zárójelen belül (axk+b)-van, a válasz: baj. Ettől kicsit elbonyolódik a dolog.
|
| Előzmény: [260] tudniakarok, 2005-03-25 23:12:48 |
|
| [260] tudniakarok | 2005-03-25 23:12:48 |
 Kérlek segítsetek! Házi volt a csonkakúp térfogatának bizonyítása integrálszámítással,na most én lusta voltam bontogatni a zárójeleket,így összetett fv. primitív fv.-ét kerestem,kijött a jó képlet,a tanárom szerint lehet hogy csak véletlen,mert hogy ő nem érti(vagy csak nem akarja gyötörni magát)! Na de a lényeg,tehát vmi ilyesmi jött ki általánosan:
![\int{(ax+b)^n}dx=\bigg[\frac1a\frac{(ax+b)^{n+1}}{n+1}\bigg]](keplet.cgi?k=32B76B09D626FA45) szerintem jó,de ha találtok vmi hibát lécci közöljétek,mert még nem csináltam túl sok ilyen példát!Előre is köszi! Ja és még egy kérdés: mi van akkor ha az intergrandusban a változó nem elsőn hanem k-adikon van,erre még nem jöttem rá!? szerintem jó,de ha találtok vmi hibát lécci közöljétek,mert még nem csináltam túl sok ilyen példát!Előre is köszi! Ja és még egy kérdés: mi van akkor ha az intergrandusban a változó nem elsőn hanem k-adikon van,erre még nem jöttem rá!?
|
|
|
| [258] Káli gúla | 2005-03-23 22:44:16 |
 Tegyük fel, hogy a sztringnek csak a "10"-zel kezdődő 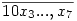 hétjegyű számokat kell tartalmaznia legalább egyszer. Rendezzük ezeket növekvő sorrendbe. A 32 db második helyiértékes 0 különböző helyre fog kerülni a sztringben, mert a mögöttük álló 5 bites számok különbözők. Az első 16 szám harmadik helyiértékes nullája is mind különböző lesz, mert a mögöttük álló 4 bites számok különbözők, ugyanígy az első 8 negyedik, az első 4 ötödik, az első 2 hatodik, az első 1 hetedik helyiértékes 0 is mind más. (Különböző helyiértékű 0-k is különbözők, mert balra különböző számú 0 valasztja el a kezdő 1-estől.) Ez összesen 32+16+...+1=63 darab nulla, tehát nincs 127-nél rövidebb sztring. hétjegyű számokat kell tartalmaznia legalább egyszer. Rendezzük ezeket növekvő sorrendbe. A 32 db második helyiértékes 0 különböző helyre fog kerülni a sztringben, mert a mögöttük álló 5 bites számok különbözők. Az első 16 szám harmadik helyiértékes nullája is mind különböző lesz, mert a mögöttük álló 4 bites számok különbözők, ugyanígy az első 8 negyedik, az első 4 ötödik, az első 2 hatodik, az első 1 hetedik helyiértékes 0 is mind más. (Különböző helyiértékű 0-k is különbözők, mert balra különböző számú 0 valasztja el a kezdő 1-estől.) Ez összesen 32+16+...+1=63 darab nulla, tehát nincs 127-nél rövidebb sztring.
|
| Előzmény: [253] jonas, 2005-03-21 22:07:57 |
|
| [257] jonas | 2005-03-22 19:33:57 |
 Hadd folytassam a tegnapi gondolatomat. Mar megallapitottuk, hogy ha pontosan 64 egyessel sikerul a feladat, akkor minden egyessel kezdodo 7-jegyu szam pontosan egyszer szerepel. Ez azt jelenti, hogy ha egy ilyen bitsorozatot abrazolunk a grafon, akkor a kapott vonalban minden olyan el pontosan egyszer szerepel, ami egy olyan csucsbol indul, ami 1-essel kezdodik. Sporolni csak azokon az eleken lehetne, amik a 0-assal kezdodo elekbol indulnak. Ezek az elek azonban az egyetlen (000000,000000) elen kivul fat alkotnak, ezert nem lehet elhagyni beloluk azon a bizonyos egy elen kivul. Ha ugyanis az egesz grafbol kivonjuk a vonalat, akkor csak a fa elei maradhatnak meg (de azok elvileg akarmilyen elojellel, hiszen lehetne, hogy egy 0-val indulo elen tobbszor megyunk at), de egy fan ez csak ugy lehetseges, ha minden el 0-szor van benne. Tehat legalabb 63 nullasra valoban szukseg van. (Ezt ennel biztos egyszerubben is be lehet latni.)
Meg egy megjegyzes. A grafos megkozelitesbol lehet sejteni, hogy valojaban nagyon sok ilyen de Bruijn kor van. Ez tenyleg igy igaz: a A016031 sorozat megadja ezek szamat.
Ebbol az is kovetkezik, hogy nagyon konnyu de Bruijn kort eloallitani: egyszeruen ki kell indulni a 0000000 sorozatbol, es utana irni veletlen biteket arra vigyazva, hogy ne vegyuk egyik 7 bites szamot sem tobbszor. Ekkor persze elofordulhat, hogy levagjuk a graf egy reszet, ezert nem tudjuk befejezni a kort, de ilyenkor egyszeruen ujra probalkozhatunk, es hamar sikerulni fog. Az elobb ezzel az egyszeru veletlen modszerrel allitottam elo a szamokat. Itt van a kod, ha valakit erdekel.
|
 |
| Előzmény: [256] lorantfy, 2005-03-22 14:51:19 |
|
| [256] lorantfy | 2005-03-22 14:51:19 |
 Kedves Jónás!
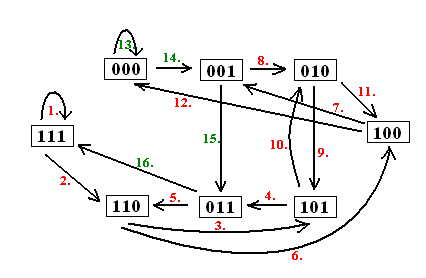
Nagyon szép a bizonyítás! Igazi "vezérlő dinamika". De nézzük meg mit is láttunk be ezzel. n=7 esetén a számjegyek 6 jegyűek és 26=64 db van belőlük, tehát a gráfnak 128 éle van. Indulunk az egyik csúcsból és bejárjuk az Euler kört. Az első szám 6 jegyű és minden élen való áthaladás egyel növeli a szám hosszát. Tehát 6+2*64=134 jegyű számot állítottunk elő, mely tartalmazza az összes 7 hosszúságú bitsorozatot, de 67 db 1-es számjegyet tartalmaz.
Példa képpen mutatom az n=4 jegyű esetet.
|
 |
| Előzmény: [255] jonas, 2005-03-21 22:57:58 |
|
| [255] jonas | 2005-03-21 22:57:58 |
 Akkor lelövöm a "vezérlő dinamikát". Nem akartam rögtön elmondani, mert ismertem (Simonyi tanár úr gyakorlatán volt feladat); hadd gondolkodjanak a "fiatalok". Azt viszont nem tudom megmondani, hogy kevesebb nullával le lehet-e írni az 1000000...1111111 számokat. (Azért elgondolkozom még rajta, most hogy a bizonyítást átgondoltam, lehet, hogy könnyű lesz.) Ha viszont megengedünk 64-nél több egyest, akkor azt hiszem hogy összesen 127-nél kevesebb számjeggyel is le lehet írni őket, de nem tudom, hány számjegy kell.
Aki tehát gondolkozni akar a 64 számjegy bizonyításán, az ne olvasson tovább.
Azt fogom belátni, hogy bármely n-re létezik ún de Bruijn-ciklus, vagyis hogy fel lehet írni egy kört 2n bitből úgy, hogy a körből n szomszédos bitet összeolvasva minden n hosszú bitsorozatot pontosan egyszer kapunk meg. Ha már tudjuk, hogy van n=7-re de Bruijn-ciklus, akkor ezt felvágva a 0000000 előfordulásának utolsó számjegyénél, egy megfelelő 127 hosszú bitsorozatot kapunk. (Azt könnyű látni, hogy pontosan 64 egyes van benne.)
Ehhez pedig vegyünk egy irányított gráfot, amelynek csúcsai az n-1 hosszú bitsorozatok, az (u,v) pedig akkor és csak akkor él, ha u utolsó n-2 bitje megegyezik v első n-2 bitjével. Ebben a gráfban van Euler-kör, mert összefüggő, és minden csúcsának megegyezik a ki- és a befoka, ugyanis mindkettő 2. Ha nézzük a gráf egy (u,v) élét, ezt jellemezhetjük egy n bites számmal, amit úgy kapunk, hogy u és v bitjeit egymásra helyezzük úgy, hogy fedjék egymást. Két szomszédos élhez két olyan szám tartozik, hogy az első él utolsó n-1 bitje éppen a második él első n bitje, ez tudniillik a közös csúcs. Ebből következik, hogy egy Euler-kör éppen egy de Bruijn körnek felel meg.
(A Konkrét Matematika egyébként egy helyen megemlíti a de Bruijn köröket, noha ahhoz a bizonyításhoz, ahol használja, valójában nincs szükség rájuk. Bizonyítást nem ad a körök létezésére, csak hivatkozik a Programozás Művészetére.)
|
| Előzmény: [254] lorantfy, 2005-03-21 22:27:17 |
|
| [254] lorantfy | 2005-03-21 22:27:17 |
 Kedves Jónás és Levi!
Örülök, hogy "rákattantatok" a problémára! Bevallom nektek, hogy én is csak n=4-jegyűig írtam fel, mint Levi és ebből gondoltam, hogy nagyobb n-ekre is igaz.
Külön gratula Jónásnak, hogy volt türelme hozzá!
Bár ez már nem ujjgyakorlat, de jó lenne, ha valaki rámutatna a "vezérlő dinamikára", szóval, hogy miért lehet ezt minden n-re megtenni!
Jó kérdés a 0-k számának csökkentése is!
|
| Előzmény: [253] jonas, 2005-03-21 22:07:57 |
|
| [253] jonas | 2005-03-21 22:07:57 |
 Az előzőben értelemszerűen 64 egyes számjeggyel értendő.
Nyilvánvaló, hogy legalább 64 egyes szükséges is, mert minden szám egyessel kezdődik. A kérdés tehát a következő: le lehet-e írni 64 egyessel, de 63-nál kevesebb nullával az összes pontosan 7-jegyű bináris számot, és ha igen, akkor hány nulla kell ehhez?
|
| Előzmény: [252] jonas, 2005-03-21 21:46:47 |
|
| [252] jonas | 2005-03-21 21:46:47 |
 Nos, 64 számjeggyel fel lehet írni őket:
1001000010101011001011011010000011001110011000011101010011110010\ 011011111110100101000110101111011000100010111011100011111000000
Azonban ez 127 számjegy, ezért nem valószínű, hogy egy fiú egy sorba fel tudja írni őket (ha több sorba írja, akkor már meg kell ismételni legalább egy 1-est). Itt a fórumon sem fért el egy sorban, ezért meg kellett törnöm. Én tehát arra szavazok, hogy Jancsi ugrat minket, valójában Juliska írta a számsort.
Lehet, hogy ennél kevesebb számjeggyel is meg lehet csinálni, nem tudom.
|
| Előzmény: [250] lorantfy, 2005-03-18 00:13:13 |
|
| [251] levi | 2005-03-21 17:22:28 |
 Sejtés a 67.b feladatra: Ha veszünk egy n számjegyű számot (csupa 0-ból és 1-ből, akkor a keresett "láncban" mindig 2n-1 darab 1-es lesz (és ekkor 2n-1-1 db 0).
n=2 esetén variációk: 11,10 a lánc:110 és 2n-1=2, azaz itt müködik
n=3 esetén variációk: 111, 110, 101, 100 a lánc: 1110100 és 2n-1=4, azaz itt is működik
n=4-re is megnéztem, azt most nem írom le, tehát ha a sejtés igaz, akkor n=7 esetén 2n-1=64 lesz. Azaz elvileg Jancsi igazat mondott.
|
| Előzmény: [250] lorantfy, 2005-03-18 00:13:13 |
|
| [250] lorantfy | 2005-03-18 00:13:13 |
 Arra gondoltam csavarként, hogy írhatja folyamatosan egymás után a számjegyeket és bármely egymás után következő hét számjegy lehet egy új 7-jegyű szám, ha 1-es áll az elején.
67.b feladat: Jancsi azt állítja, hogy sikerült felírnia az összes 7 jegyű 1 és 0 számjegyből álló számot 64 db 1-es felhasználásával? Igaza van-e Jancsinak?
|
| Előzmény: [249] Csimby, 2005-03-17 16:20:45 |
|
|
| [248] lorantfy | 2005-03-17 13:44:39 |
 Az első számjegy csak 1-es lehet a további 6 helyiértéken pedig 0 vagy 1, tehát kétféle számjegy állhat. Így 26=64 db ilyen szám van. Írjuk egymás alá ezeket a számokat. Az első oszlopban 64 db 1-es van a többi oszlopban pedig a számjegyek fele 1-es fele 0. Így 64+6*32=256-szor kellett Jancsinak leírnia az 1-es számjegyet.( Feltéve persze, hogy nincs valami trükk a felírásban, ami Csimbytől azért elvárható! )
|
| Előzmény: [247] Csimby, 2005-03-16 23:17:14 |
|
| [247] Csimby | 2005-03-16 23:17:14 |
 67.feladat Jancsi felírta az összes olyan hétjegyű egész számot, amely csak 0 és 1 számjegyeket tartalmaz. Hányszor írta le az 1-es számjegyet?
|
|
|
| [245] Kalmár-Nagy József | 2005-03-01 13:16:32 |
 Ha a-1,a,a+1 köbeit vesszük és rendezzük, elegánsabban kijön. Átalakítások után azt kapjuk, hogy a2(a-6)=2. (az a után a 2 a négyzetet jelölné, csak még lusta voltam a TeX-et megtanulni :) A szorzat mindét tagja egész, mert 'a' is az. Az egyes eseteket gyorsan végig lehet futni.
|
|
| [244] Csimby | 2005-02-28 23:36:21 |
 Suhanc egyenletét és a kongruencia szabályait felhasználva:
Ha a 0 maradékot ad 4-gyel osztva, akkor a bal oldal osztható 4-gyel, a jobb oldal 3 maradékot ad 4-gyel osztva.
Ha a 1 maradékot ad 4-gyel osztva, akkor a bal oldal 1 maradékot, a jobb oldal 3 maradékot ad 4-gyel osztva.
Ha a 2 maradékot ad 4-gyel osztva, akkor a bal oldal osztható 4-gyel, a jobb oldal 1 maradékot ad 4-gyel osztva.
Ha a 3 maradékot ad 4-gyel osztva, akkor a bal oldal 3 maradékot, a jobb oldal 1 maradékot ad 4-gyel osztva.
Mind a 4 esetben ellentmondásra jutottunk, tehát nincsen olyan a amely eleget tenne a feltételeknek.
|
| Előzmény: [242] Suhanc, 2005-02-28 21:00:37 |
|
| [243] Atosz | 2005-02-28 22:00:32 |
 Kedves László és Suhanc!
Nem tudom, hogy mennyire elegáns vagy nem, de a nagy Fermat sejtés (illetve ma már tétel) nem elég erre? Azaz az xn+yn=zn-nek n>2 esetén nincs megoldása.
|
| Előzmény: [241] lorantfy, 2005-02-27 15:38:28 |
|
| [242] Suhanc | 2005-02-28 21:00:37 |
 Kedves László!
Egy nem túl elegáns megodásom lenne a feladatodra:
Legyen a három egymást követő köbszám a3,(a+1)3és(a+2)3 ! Adjunk felső korlátot a értékére, majd a maradék eseteket megvizsgáljuk a végén. A feladat állítása szerint (rendezve az egyenletet):
a3=3a2+9a+7
Bonsuk a3-t három egyenlő részre, mert a jobb oldalon három tag van. Nyilván, ha

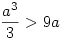
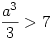
feltételek egyszerre teljesülnek, az egyenletnek nem lehet megoldása, hisz a bal oldal határozottan nagyobb. A három egyenlőtlenség közül az első a legenyhébb, ezért a>9 esetén biztosan nincs megoldás.
Maradt tehát 10 esetünk 0-tól 9 ig. Ezeket behelyettesítve az egynletbe nem kapunk kielégítő megoldást, ezzel a feladat állítását bizonyítottuk.
|
| Előzmény: [241] lorantfy, 2005-02-27 15:38:28 |
|
| [241] lorantfy | 2005-02-27 15:38:28 |
 66. feladat: Bbh. három egymást követő természetes szám közül a legnagyobb köbe nem lehet egyenlő a másik kettő köbének összegével.
|
|
|
| [239] Suhanc | 2005-01-08 08:56:51 |
 Az 55.Feladat szemmel láthatólag nem hozott lázba senkit...;)
Ha esetleg valaki mégis lenne olyan "elvetemült", egy kis segítség:
Ez egy olyan "közepes" feladat...
|
|
| [238] Suhanc | 2005-01-08 08:52:43 |
 Kedves Mindenki!
Ez egy olyan apró gondolat... de szép!:)
65.Feladat:
Igazoljuk, hogy :
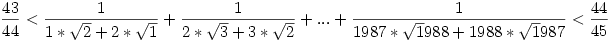
|
|
| [237] lorantfy | 2004-12-21 00:27:58 |
 Páros n-re is igaz lesz, mert ekkor k>n és n végén k-n db 0 áll.
Ekkor viszont (2k-1-n) végén k-n db 1-es fog állni előttük (balra) 0 áll. Így +1 hozzáadása (k-n) db 1-esből 1 db 1-est csinál. A változás -(k-n)+1 a számjegyek összegében.
A számjegyek összege: (m-1)+(k-m)-(k-n)+1=n.
|
| Előzmény: [236] lorantfy, 2004-12-21 00:02:58 |
|











