| [327] hobbymatekos | 2005-09-22 20:54:13 |
 Kiintegrálható. Többféleképp is. De van elemi megoldás is talán, mindenféle integrálgatás nélkül :)). Megnézem ha lesz időm. Egyébként nagyon szépen intható akár gömbkoo., akár hengerkoo.-ban is, de ahogy felirtam, akár táblázatból is "favágással", sőt igy első ránézésre akár a Komplexben is (persze csak a valós része értelmes). Mint emlitettem ennél bonyolultabbak voltak vizsgabeugrók. Na most a gyakorló matematikusok valahogy nemigen kedvelik az integrálgatást (persze néha muszály..., de akkor is meggondolandó előtte, mire jó az eredmény, de persze van aki szeretheti is.) Mérnöki gyakorlatban sem kell már annyira, mert a szükséges pontossággal minden lényeges adatot (térfogat, felszin, súlypont, statikai nyomatékok, másodrendű nyomatékok stb. CAD rendszer megadja. Iskolában persze tudni kell. (Diffegyenletekhez főleg, és ne feledjük, nem minden integrál létezik zárt alakban)
Addig is új feladat:
a) Mennyi az n dimenziós gömb és az n dimenziós kocka térfogata,valamint térfogatuk aránya?
b)ugyanez végtelen dimenzióban (n tart végtelen határérték)
(mérnök-fizikusoknak ajánlott... Meglepő lesz az eredmény, ugyhogy nem biztos, hogy rosszul számoltál.)
|
| Előzmény: [326] Lóczi Lajos, 2005-09-22 19:40:29 |
|
| [326] Lóczi Lajos | 2005-09-22 19:40:29 |
 Valakitől hallottam, hogy pár éve ez egy vizsgapélda volt, persze több más feladat kíséretében. Szóval nem volt korlátlan idő a megoldásra és számítógép sem kéznél. A kérdéses test egyébként a Viviani-féle test. (Én a térfogatot egy kicsit más integrállal írtam fel, és első nekifutásra nem is tudtam elemien kiszámolni, csak másnap másodikra másképp elindulva, pedig számítógépet is használtam. Az Általad felírt alakot egyébként a gép ki tudta számolni és a kétféle módszerrel kapott eredmény ugyanannak bizonyult.)
|
| Előzmény: [325] hobbymatekos, 2005-09-22 16:26:39 |
|
| [325] hobbymatekos | 2005-09-22 16:26:39 |
 Ja vagy úgy:)) leesett. Nem gondoltam, hogy a számérték lényeges. Szóval egy ilyen határozott integrált többféle módon ki lehet számolni: 1. Feladjuk valamelyik fórumba. 2. Elhireszteljük ez lesz a következő ZH példa. (Egy egész kolesz egy éjszaka alatt csak megcsinálja) 3. Mégegyszer átgondoljuk: nem elégséges nekünk csupán egy becslés? 4. Előveszünk egy integráltáblázatot és bizunk benne nem nyomdahibás 5. Ha minden kötél szakad akkor is alszunk rá egyet 6. Ha nagyon muszálz, akkor keresünk egy nyugodt helyet és nekiesünk... Ez még szelid fajta... Macerás lesz beirni TeX-be.... Utoljára vizsgabeugró feladatként volt ilyen élményem néhány táblán keresztül...:))
|
| Előzmény: [324] hobbymatekos, 2005-09-22 15:49:56 |
|
|
|
|
|
| [320] Lóczi Lajos | 2005-09-22 01:45:25 |
 (Ha már gömböknél meg kúpoknál tartunk, még egyszer beírok egy régebbi feladatot, ami még nem lett megoldva.)
Adjuk meg annak a testnek a térfogatát, amit egy (végtelen) henger metsz ki egy gömbből, ha a henger sugara épp fele a gömb sugarának és a henger palástja érinti a gömb középpontját, valamint a gömbfelület egy pontját.
|
|
| [319] Lóczi Lajos | 2005-09-22 00:29:03 |
 Nem "kell" a szélsőértékszámítás, csak én ezt az utat választottam: meg szeretném mutatni, hogy egy kifejezés nemnegatív. Ezt úgy láttam be, hogy megmutattam, a kifejezésnek van minimális értéke, ami éppen nulla.
|
| Előzmény: [317] hobbymatekos, 2005-09-21 15:58:02 |
|
| [318] hobbymatekos | 2005-09-21 17:06:51 |
 Mivel unalmas volna a jobboldal minden 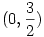 értékére végigvizsgálgatni (talán nem hiba ilyet ide irni, hiszen itt messze az egyetemi mat. tananyagban járatos középiskolások vannak): értékére végigvizsgálgatni (talán nem hiba ilyet ide irni, hiszen itt messze az egyetemi mat. tananyagban járatos középiskolások vannak):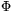 (x,y,z) skalár-pont fv. (skalármező), egyetlen szakadása van origóban ,ez a fv. grad (x,y,z) skalár-pont fv. (skalármező), egyetlen szakadása van origóban ,ez a fv. grad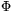 =const. szintvonalaival szemléltethető. Ez viszont már olyan vektormező, amely vektorvonalait dr x nabla ( =const. szintvonalaival szemléltethető. Ez viszont már olyan vektormező, amely vektorvonalait dr x nabla (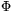 )=0 ill. )=0 ill. 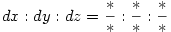 diffegyenleteknek eleget tesz.(x vektoriális szorzat) vagyis diffegyenleteknek eleget tesz.(x vektoriális szorzat) vagyis 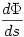 iránymenti derivált nagysága |nabla iránymenti derivált nagysága |nabla 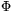 |. Itt a * helyére a megfelelő változók szerinti parciális deriváltak értendők. (Ha igy megy tovább, akkor a TeX készlet jelentős bővitésre szorul :-) A nablát igy is kiirtam, dr vektor, és a nulla is vektor, nabla |. Itt a * helyére a megfelelő változók szerinti parciális deriváltak értendők. (Ha igy megy tovább, akkor a TeX készlet jelentős bővitésre szorul :-) A nablát igy is kiirtam, dr vektor, és a nulla is vektor, nabla 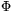 is ) A gradiensvonalak a szintfelületetket merőlegesen metszik. Ennél több önmagában nem mondható el erről a kifejezésről. Akkor mit is mond a Titu lemma? is ) A gradiensvonalak a szintfelületetket merőlegesen metszik. Ennél több önmagában nem mondható el erről a kifejezésről. Akkor mit is mond a Titu lemma?
|
|
| [317] hobbymatekos | 2005-09-21 15:58:02 |
 Na ez már más. Ugyanis aközött választani kell, explicite, vagy implicite adom meg a függvényt. Ha csak lehet, explicite. Nyilván másképp kell deriválni a két esetben. Ha imlicite adjuk meg, akkor azokban és csak azokban a pontokban mondhatunk bármit is ami az implicit összefüggést mint feltételt kielégiti. (Tehát implicit fv differenciálása cimü fejezetet aki nem ismeri nézzen utána) Ez a kifejezés az egész térben pozitiv. A következő gondom az volt: miért kell itt a szélsőértékszámitás??
|
| Előzmény: [315] Lóczi Lajos, 2005-09-21 12:03:21 |
|
| [316] Lóczi Lajos | 2005-09-21 12:08:55 |
 A legkisebb felső korlát a megsejtett 3/2, ugyanis az
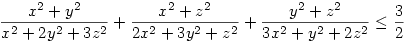
egyenlőtlenség ekvivalens ezzel
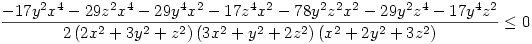
ami nyilván igaz.
Ebből az is látszik, hogy egyenlőség pontosan akkor áll, ha a három változóból kettő nulla, egy pedig nemnulla.
|
| Előzmény: [313] Suhanc, 2005-09-20 21:15:44 |
|
| [315] Lóczi Lajos | 2005-09-21 12:03:21 |
 Az eredeti háromváltozós kifejezésben elvégzek egy változóhelyettesítést. (Feledkezzünk el mindenféle geometriáról, meg "azonosan 1 függvényről").
Ezzel a háromváltozós feltétel nélküli szélsőértékprobléma egy kétváltozós szélsőértékfeladattá egyszerűsödik, egy zárt síkbeli téglalap fölött. (A helyettesítő függvények határpontokban vett deriválhatósága nem kérdéses: a téglalap periodikusan kiterjesztető, és ekkor  és és  az egész síkon vannak értelmezve, de minket úgyis csak az eredeti téglalapon vett viselkedésük érdekel.) Azért nem kell feltételes szélsőértékszámítást alkalmazni, mert a zárt téglalap határán a g függvény viselkedését külön megvizsgáltam, ahol kiderült, hogy határozottan pozitív. A téglalap belseje nyílt halmaz, tehát itt a közönséges szélsőértékszámítás által megtalált egyetlen lokális minimum kell legyen g minimuma. az egész síkon vannak értelmezve, de minket úgyis csak az eredeti téglalapon vett viselkedésük érdekel.) Azért nem kell feltételes szélsőértékszámítást alkalmazni, mert a zárt téglalap határán a g függvény viselkedését külön megvizsgáltam, ahol kiderült, hogy határozottan pozitív. A téglalap belseje nyílt halmaz, tehát itt a közönséges szélsőértékszámítás által megtalált egyetlen lokális minimum kell legyen g minimuma.
|
| Előzmény: [314] hobbymatekos, 2005-09-21 11:01:41 |
|
| [314] hobbymatekos | 2005-09-21 11:01:41 |
 Természetesen igazad van. Csakhogy: a gömbi kook.-at differenciáltad.A gömbi kook:origó középpontú gömbök,origó csúcsú körkúpok, és z
tengelyen átmenő sikok.Illetve ezek metszésvonalai metszéspontja felel meg egy pont Descartes koo.-nak. Az, hogy a DESCARTES derékszögü kook. és a a fenti másodrendü felületek között mi a
kapcsolat, abból jönnek azok a formulák amit felirtál. Azzal kapcsolatban annyi megjegyzést tennék: z=Rcos( ) az iránykoszinuszok miatt a szokásos alak. (Bár szinusszal is igaz).Továbbá ) az iránykoszinuszok miatt a szokásos alak. (Bár szinusszal is igaz).Továbbá  tehát [0;2 tehát [0;2 )-beli A koordinátadifferenciálok transzformációja viszont más lesz. Feltételes )-beli A koordinátadifferenciálok transzformációja viszont más lesz. Feltételes
szélsőértékszámitás (Lagrange multiplikátormódszer) kellene, (abszolut) helyett. Maga az azonosan egy csak egydimenzióban egyértelmü.Tehát a számegyenesen. Vagy : a 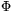 (x,y,z) deriváltját irdd át gömbi koo-ba. Arra pedig absz. szélsőértékszámitás. A többivel ennek tisztázása után érdemes foglalkozni... (x,y,z) deriváltját irdd át gömbi koo-ba. Arra pedig absz. szélsőértékszámitás. A többivel ennek tisztázása után érdemes foglalkozni...
|
| Előzmény: [307] Lóczi Lajos, 2005-09-18 20:24:29 |
|
| [313] Suhanc | 2005-09-20 21:15:44 |
 Nem a legjobb felső korlát, de sztem a 3-at nem éri el, hiszen mindhárom tagban kisebb a számláló a nevezőnél...tehát a kifejezés korlátos... most megkérdezhetjük, mi a legkisebb felső korlát...
|
| Előzmény: [306] hobbymatekos, 2005-09-17 23:37:21 |
|
|
| [311] rizsesz | 2005-09-19 00:44:55 |
 csendben hallgatok, vissza.
|
|
| [310] rizsesz | 2005-09-18 23:04:48 |
 Ömm. Lehetséges, hogy az utolsó lépéssel nem értek egyet? :) Mármint nem 1>=xyz esetén lenne igaz, amit leírtál? elnézést, ha hülyeséget mondtam, no meg textelenségért. rizsa
|
| Előzmény: [295] SAMBUCA, 2005-09-12 00:34:20 |
|
| [309] hobbymatekos | 2005-09-18 22:48:52 |
 Az eredetileg Suhanc által felirt képlet bal oldala. A koordinátatengelyekben azaz a) x=0,y=0,z nem nulla tetszőleges akkor a kifejezés értéke 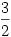 és persze a szimmetria miatt minden tengelyre igaz. Ha jól látom. Vagyis origó és persze a szimmetria miatt minden tengelyre igaz. Ha jól látom. Vagyis origó  sugarú környezetében és egy egységgömb közötti tartományban amennyiben 1-et nem visszük baloldalra a lokális maximum sugarú környezetében és egy egységgömb közötti tartományban amennyiben 1-et nem visszük baloldalra a lokális maximum 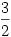 Azaz az egységgömb első térnyolcadba eső része, a koo sikok, ill. az xz sikkal 45 fokos hajlásszögü sikkal kettémetszet nyolcadgömb (azaz végülis két 16-od gömbcikk) mint térbeli tartományban valamint az (1,2,3), (2,3,1), (3,1,2) pontokba mutató helyvektorok mint oldalélek által meghatározott háromszög alapú gúla, mint térbeli tartományok közötti térben vizsgálódnék. Azaz az egységgömb első térnyolcadba eső része, a koo sikok, ill. az xz sikkal 45 fokos hajlásszögü sikkal kettémetszet nyolcadgömb (azaz végülis két 16-od gömbcikk) mint térbeli tartományban valamint az (1,2,3), (2,3,1), (3,1,2) pontokba mutató helyvektorok mint oldalélek által meghatározott háromszög alapú gúla, mint térbeli tartományok közötti térben vizsgálódnék.
|
| Előzmény: [308] Lóczi Lajos, 2005-09-18 20:28:11 |
|
|
| [307] Lóczi Lajos | 2005-09-18 20:24:29 |
 Nem értem, mi nem stimmel.
A gömbi koordinátákat a régi x,y,z változók helyére helyettesítjük, a konstans 1 nem tartalmaz ilyet, nem kell semmilyen gömbfelületként sem felfogni, csak puszta számként.
|
| Előzmény: [301] hobbymatekos, 2005-09-16 21:06:45 |
|
| [306] hobbymatekos | 2005-09-17 23:37:21 |
 Mutassuk meg,hogy 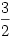 értéket is felveszi. a) adjuk meg, ezen pontok mértani helyét b) döntsük el, hogy felülről korlátos e a kifejezés c) ha igen, adjuk meg a felső korlátot értéket is felveszi. a) adjuk meg, ezen pontok mértani helyét b) döntsük el, hogy felülről korlátos e a kifejezés c) ha igen, adjuk meg a felső korlátot
|
| Előzmény: [304] Suhanc, 2005-09-17 20:30:11 |
|
|
| [304] Suhanc | 2005-09-17 20:30:11 |
 Az említett margó(m):
Csimbyhez hasonlóan én is a számlálóknak adtam új jelölést, ezáltal a már említett
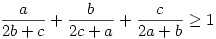
egyenlőtlenséget kapva. Ezután viszont inkább megint bevezettem egy új jelölésrendszert, remélve, hogy a feltételek felrúgása nélkül kaphatunk egyszerűbb alakot:
2b+c=p 2c+a=q 2a+b=r
alapján kapjuk, hogy
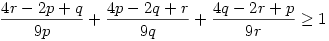
Melyet megfelelő módon átalakítva kapjuk, hogy:
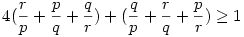
Mivel p, q, r nemnegatív számok, a két zárójelet számtani-mértani középpel lebecsülve a bizonyítandó állítást kapjuk.
|
| Előzmény: [300] Lóczi Lajos, 2005-09-15 20:53:41 |
|
| [303] Suhanc | 2005-09-17 20:15:14 |
 Kedves Mindenki!
Kissé megkéstem ezzel a hozzászólással. Így utólag is szeretném megköszönni mindenkinek az érdekes megoldásokat és hozzájuk kapcsolódó hozzászólásokat. Azontúl, hogy általánosságban is megmozgatta az állóvizet, nekem személyesen sok újat mutatott (pl: az emlegetett Titu-lemma). A konkrét sztorit eddig szándékosan nem írtam le a feladathoz: matektáborban ifiként tevékenykedtem, egy 9. osztályos tanuló pedig felajánlott nekem egy tábla csokit, ha megoldom belátható időn belül ezt a feladatot. A megoldás megbeszélése után említette, hoyg ő ezt Cauchy-Schwarz-Bunyakovszkij egyenlőtlenséggel meg tudja csinálni rövidebben. "Egy tábla csokiért elárulom"-mosolygott. Azonban a csoki, amelyret már gondolatban szétosztottunk az ifistársak közt, nagyon hívogató volt, ezért lemondtam (szégyen, gyalázat) a megoldásról. Reméltem, hogy elő fog kerülni...
|
|




 (x,y,z) skalár-pont fv. (skalármező), egyetlen szakadása van origóban ,ez a fv. grad
(x,y,z) skalár-pont fv. (skalármező), egyetlen szakadása van origóban ,ez a fv. grad és
és  az egész síkon vannak értelmezve, de minket úgyis csak az eredeti téglalapon vett viselkedésük érdekel.) Azért nem kell feltételes szélsőértékszámítást alkalmazni, mert a zárt téglalap határán a g függvény viselkedését külön megvizsgáltam, ahol kiderült, hogy határozottan pozitív. A téglalap belseje nyílt halmaz, tehát itt a közönséges szélsőértékszámítás által megtalált egyetlen lokális minimum kell legyen g minimuma.
az egész síkon vannak értelmezve, de minket úgyis csak az eredeti téglalapon vett viselkedésük érdekel.) Azért nem kell feltételes szélsőértékszámítást alkalmazni, mert a zárt téglalap határán a g függvény viselkedését külön megvizsgáltam, ahol kiderült, hogy határozottan pozitív. A téglalap belseje nyílt halmaz, tehát itt a közönséges szélsőértékszámítás által megtalált egyetlen lokális minimum kell legyen g minimuma. )-beli A koordinátadifferenciálok transzformációja viszont más lesz. Feltételes
)-beli A koordinátadifferenciálok transzformációja viszont más lesz. Feltételes 

 sugarú környezetében és egy egységgömb közötti tartományban amennyiben 1-et nem visszük baloldalra a lokális maximum
sugarú környezetében és egy egységgömb közötti tartományban amennyiben 1-et nem visszük baloldalra a lokális maximum 