Fórum: "ujjgyakorlatok"

De igenis "ujjgyakorlatok", programozási ujjgyakorlatok és "keress szabályszerűségeket a gép outputjában"-ujjgyakorlatok :) -- amíg nincs bizonyítás, addig biztosan.

Talán nyithatnátok egy új topic-ot a témának, mert már nem igazán ujjgyakorlatok :-)

Euler sejtés: Ha s2 és x₁,...,x_s,z,n pozitív egészek és x₁ⁿ+x₂ⁿ+...+x_sⁿ=zⁿ, akkor s n.

Ha ez igaz lenne, akkor következne belőle a Fermat-sejtés vagy Wiles-tétel ;-) is, azonban 1966-ban L.J. Lander és T.R. Parkin amerikai matematikusok találtak egy ellenpéldát (n=5,s=4):

a⁵+b⁵+c⁵+d⁵=144⁵

Keressük meg a megfelelő a,b,c,d pozitív egészeket. Az n=4,s=3 esetre az előbb említett két úr és J.L. Selfridge már 1967-ben megmutatták, hogy a x₁⁴+x₂⁴+x₃⁴=z⁴ egyenletnek biztosan nincs olyan pozitív egész megoldása, ahol x₁,x₂,x₃,z mindegyike kisebb, mint 220000. Az első ellenpéldát Noam Elkies adta és megegyezik a 74. feladattal ([341]. hozzászólás). A legkisebb ismert ellenpéldát (n=4,s=3 esetén) R.Frye adta, és a [345]-ös hozzászólásban szerepel.

Igen nekem is ezek jöttek ki minimális cáfolómodulusnak; esetleg valami sejtés általában? :) Ha lesz időm, beírom az én 2 apró megfigyelésem.

Az első esetben mod(311), a másodikban mod(709) jónak tűnik

Elkezdett foglalkoztatni, hogy hogyan lehet olyan modulusokat keresni, amelyek azt mutatják, hogy egy

x^p+y^q=n

alakú diofantoszi egyenletnek nincs megoldása. Mivel egy egysoros programmal sikerült jelentősen automatizálni az egyenletek átvizsgálását, több sejtést is kialakítottam. Ezeket hamarosan beírom ide. Addig is, álljon itt két újabb egyenlet, amelyek bizonyos szempontból a "legrosszabbul" viselkednek (minimális fokszám mellett a legnehezebb cáfolni a megoldásuk létét):

Oldjuk meg az egész számok körében az

x³¹+y³¹=31

egyenletet. Ugyanez a kérdés vonatkozik az

x⁵⁹+y⁵⁹=3

egyenletre.

Megtaláltam, amire utaltál:

41³=40³+17³+2³=33³+32³+6³,

de a 41 eme tulajdonsága hogyan kapcsolódik (ha egyáltalán) az x⁴+y⁵=1728 egyenlethez? Hiszen ezt az egyenletet úgy csináltam, hogy olyan legyen, hogy csak viszonylag "nagy" modulussal lehessen cáfolni, de az 1728 helyett a jobb oldalon nyugodtan lehetne 6 is (mivel ez kongruens 1728-cal modulo 41). Az 1728-nak számomra tehát semmi köze a 41-hez, csak azért választottam, hogy hamis asszociációkat keltsek. A mondandódból viszont az tűnik ki, mintha az 1728-ból jutott volna valahogy eszedbe a 41, mint cáfoló modulus. Ez vajon véletlen, vagy van valami a háttérben?

De azt nem látom, hogy mi a kapcsolat a két egyenlet (azaz a 4.-5. hatványos és a köbösszeges) között? Mire lehet következtetni a másikra nézve, ha tudjuk, hogy az egyiknek mi a megoldása/nincs megoldása?

A "12³-höz hasonlóan" szövegrész törlendő. Elnézést.

Egyrészt az x⁴+y⁵=1728 egyenletnek nincs megoldása mod 41, másrészt, a 12³-höz hasonlóan a 41³ is többféleképpen írható fel, de nem két, hanem három köbszám összegeként.

Valóban, fel is van sorolva a listában (ami nem rendezett).

Talán kiszámolom, ha kevésbé vagyok fáradt.

Miért, az x³+y³+z³=41³ egyenletről mit lehet tudni? (És hogyan kapcsolódik az x⁴+y⁵=1728-hoz? Kíváncsi lettem.)

Ez poén, beismerem ezzel a konstrukcióval még nem találkoztam.

De épp a 40-nél kár lenne abbahagyni a keresést. Erre próbáltam tegnap is célozgatni, a 41³=x³+y³+z³ egyenlet megoldásszámával.

Sajnos a megoldásod hibás: az első számkupacban ott az 1-es, míg a másodikban a 7-es, és 1+7=8.

Jé, tényleg elrontottam valamit.

A 40 modulus jó: x⁴mod 40 lehet 0, 1, 16, 25

y⁵mod 40 lehet 0, 1, 32, 3, 24, 5, 16, 7, 8, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39

Így aztán x⁴+y⁵mod 40 lehetséges értékei 0, 1, 32, 3, 24, 5, 16, 7, 8, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 2, 4, 6, 10, 12, 14, 18, 20, 22, 26, 28, 30, 34, 36, 38.

1728mod 40=8 nincs ezek között.

Pedig lehet. Segítség: cáfoljuk meg a megoldás létezését, hogy az egyenletet egy alkalmas maradékosztály felett nézzük.

Ha már a pitagoraszi számhármasokról van szó, mutatok egy módszert, ahogy elő lehet állítani őket. Legyen a,b egészek.

|b+ai|=|a+bi|

ezért

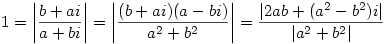
tehát a számláló és a nevező négyzete egyenlő:

(2ab)²+(a²-b²)²=(a²+b²)²

Ez persze nem bizonyítja, hogy csak ilyen alakúak lehetnek (konstans szorzótól eltekintve).

Átrendezve x⁴+y⁵=1728.

Ez érdekes egyenlet: nem tudom modulusokkal megcáfolni, de megoldást sem találtam rá (próbálgatással). Kis megoldás úgy tűnik nincs egyikre sem.

Itt egy érdekes adalék az eredeti problémához.

Legyenek a,b,c pitagoraszi számhármasok, azaz a²+b²=c². Ekkor

(ab)⁴+(ac)⁴+(bc)⁴=a⁴b⁴+c⁴(a⁴+b⁴)=a⁴b⁴+c⁴((a²+b²)²-2a²b²)=a⁴b⁴-2a²b²c⁴+c⁸=(c⁴-a²b²)²

Tehát a x⁴+y⁴+z⁴=t² egyenletnek végtelen sok megoldása van, ellentétben az x⁴+y⁴=t² egyenlettel,aminek egy sincs.

Igen, direkt szerepeltettem olyan számokat, amelyek utalnak taxicab-number-ekre, de ezt csak szándékos megtévesztésnek szántam :-), szerintem köbszámokhoz az egésznek nincs sok köze.

Természetesen próbálgattam. (A nemlineáris diofantoszi egyenletek elmélete tele van ad hoc módszerekkel, és szerintem a legnehezebb matematikák közé tartozik. Elképzelhető persze, hogy az algebrai görbék vagy varietások elméletével lehetne valamit mondani általában, de ehhez nem konyítok, messze meghaladja a képességeimet.)

Érdekes szám ez, főleg így rendszám alakba normálva :) A problémás modulus köbe többféleképp írható fel három pozitív köbszám összegeként?

A 13 honnan jött? Elkezdtél próbálgatni vagy van valami okosabb módszer?

Akkor én is generáltam egy egyenletet, ami megoldandó az egészek körében:

x⁴+y⁵+1=10³+9³.

Nem a kicsiség számít, hanem a maradékosztályok :)

Az egyenletnek nincs egész megoldása, ugyanis nézzünk mindent modulo 13:

egy negyedik hatvány 13-mal maradékosan osztva négyféle maradékot adhat, nevezetesen {0,1,3,9} valamelyikét,

egy harmadik hatvány 13-mal maradékosan osztva ötféle maradékot adhat: {0,1,5,8,12} valamelyikét,

viszont 19¹⁹ maradékosan osztva 13-mal 7-et ad.

És a 7 nem áll elő két olyan szám összegeként, amelyben az első tag az első halmazból, a második a másodikból van véve.