| [486] Lóczi Lajos | 2005-11-29 21:46:18 |
 97. kérdés. Vajon véges-e az alábbi összeg?
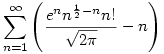
|
|
| [485] Róbert Gida | 2005-11-27 11:45:39 |
 96. feladatra
(2n+1)!=(2n+1)*(2n)!-ként felírva és használva a Stirling formulát kapjuk, hogy az eredeti sor pontosan akkor konvergens, ha az 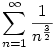 sor konvergens, viszont ez utóbbi konvergens, így az eredeti is az. sor konvergens, viszont ez utóbbi konvergens, így az eredeti is az.
Mathematica 5.1 a sor összegét is ki tudja számolni! Eszerint 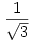 az összeg értéke. az összeg értéke.
|
|
| [484] Lóczi Lajos | 2005-11-27 09:53:41 |
 96. feladat. Véges vagy végtelen-e az alábbi összeg értéke?
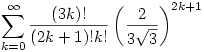
Ha igen, miért?
|
|
|
| [482] Lóczi Lajos | 2005-11-25 17:18:59 |
 Sajnos a feladat ilyen formában végtelenül nehéz lenne, és a keresett a paraméterértékeket pontosan nem lehetne behatárolni. Hogy "ujjgyakorlat" legyen, hagyjuk ki a vizsgálatból azokat az a-kat, amelyek (-2,-1)-be esnek.
|
| Előzmény: [481] Lóczi Lajos, 2005-11-25 14:04:25 |
|
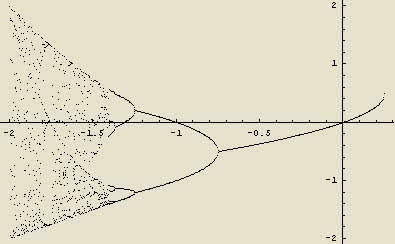
| [481] Lóczi Lajos | 2005-11-25 14:04:25 |
 Na, még egy utolsó ilyet: vizsgáljuk a Mandelbrot-halmaz valós síkmetszetét.
95. feladat. Legyen a rögzített valós szám és tekintsük az x0:=0, xn+1:=xn2+a rekurziót. Adjuk meg azokat az a értékeket, melyekre az xn sorozat
a.) konvergens. Mi ekkor a limesze?
b.) korlátos.
c.) divergens.
|
|
|
|
| [478] Ali | 2005-11-25 11:52:21 |
 Megoldás 78. -ra:
x0=0 és  . .
a.) 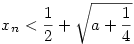 teljes indukcióval igazolható. teljes indukcióval igazolható. 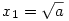 -ra igaz. Tfh n-re igaz. -ra igaz. Tfh n-re igaz. 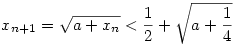 -t kell igazolni. Négyzetreemelés és rendezés után pontosan az -t kell igazolni. Négyzetreemelés és rendezés után pontosan az 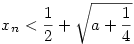 egyenlőtlenséget kapjuk, amely az indukciós feltevés miatt teljesül. egyenlőtlenséget kapjuk, amely az indukciós feltevés miatt teljesül.
Továbbá xn monoton növő, ugyanis
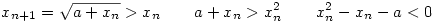
kellene, ami teljesül is, mivel xn az x2-x-a=0 egyenlet gyökei között van: 
Egy monoton növő felülről korlátos sorozatnak létezik határértéke, esetünkben ez az  egyenlet pozitív gyöke. egyenlet pozitív gyöke. 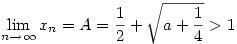
b.) Teljes indukcióval igazoljuk, hogy 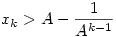 , k>0. Ez k=1 -re igaz, mert , k>0. Ez k=1 -re igaz, mert
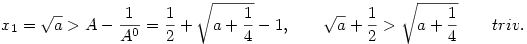
Tfh k -ra igaz.
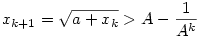
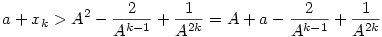
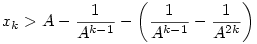
teljesül egyrészt az indukciós feltevés , másrészt a zárójelben levő kifejezés pozitív volta miatt.
Legyen 1> >0 és k olyan, hogy >0 és k olyan, hogy 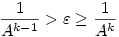 . Ilyen k létezik. Ekkor . Ilyen k létezik. Ekkor 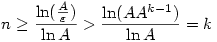
n>k miatt n k+1 és k+1 és 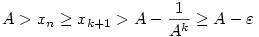 . Ezért |A-xn|< . Ezért |A-xn|<
c.) Megmutatjuk teljes indukcióval, hogy 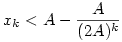 . Ez k=1 -re jó, mert . Ez k=1 -re jó, mert
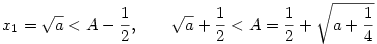
Tfh k -ra igaz,ekkor
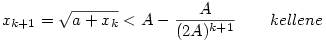


teljesül az indukciós feltevés miatt.
Legyen 1> >0 és k olyan, hogy >0 és k olyan, hogy 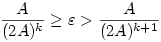 . Ilyen k létezik. Ekkor . Ilyen k létezik. Ekkor  . .
Tehát 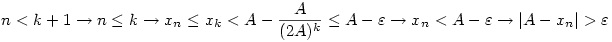
|
| Előzmény: [396] Lóczi Lajos, 2005-10-30 20:46:24 |
|
|
| [476] Lóczi Lajos | 2005-11-21 20:45:01 |
 Szép. Nagyon kíváncsi vagyok, hogyan jöttél rá (én eredetileg okos számítógép segítségével). De persze utólag meg lehet találni az explicit képletet, l. pl.
http://mathworld.wolfram.com/NewtonsIteration.html
Azt írja: "has the clever closed-form solution..."
Itt "area tangens hiperbolikusszal" van megadva, de ez, mint tudjuk, kifejezhető a logaritmussal.
|
| Előzmény: [473] Ali, 2005-11-21 15:54:56 |
|
|
| [474] Róbert Gida | 2005-11-21 17:05:43 |
 Maple 9.5 és Mathematica 5.1 sem tudja kiszámolni!!! Stirling formulából adódik, hogy 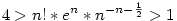 ha n nagy. Így írhatjuk, hogy az eredeti sor pontosan akkor konvergens, ha ha n nagy. Így írhatjuk, hogy az eredeti sor pontosan akkor konvergens, ha 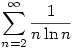 konvergens, viszont ez utóbbi sorról integrálközelítő összegekkel ismert, hogy divergens, így az eredeti sor is az. konvergens, viszont ez utóbbi sorról integrálközelítő összegekkel ismert, hogy divergens, így az eredeti sor is az.
Érdekes, de még ez utóbbi sorról sem tudja a Mathematica, hogy divergens, így ez a fő oka, hogy nem tudja kiszámolni. Kipróbáltam a Stirling formulát ismeri, tehát el tud elvileg jutni a mi összegünkig, de tovább nem. Ekkor próbáltam ki, hogy mit ad a primek reciprokösszegére és ez a megdöbbentő, hogy ezt sem ismeri, aminek most talán nem az az oka, hogy ezt a sorösszeget nem ismeri, hanem az, hogy idáig el sem tud jutni!!! mert nem ismeri azt az alapvető formulát, hogy  teljesül, ahol pn az n-edik prím ( ez egyébként a prímszámtételből adódik ). Bár ismert persze elemi bizonyítás a prímek reciprokösszegének a divergenciájára Erdős Páltól például. teljesül, ahol pn az n-edik prím ( ez egyébként a prímszámtételből adódik ). Bár ismert persze elemi bizonyítás a prímek reciprokösszegének a divergenciájára Erdős Páltól például.
|
| Előzmény: [471] Lóczi Lajos, 2005-11-21 14:32:42 |
|
|
| [472] Ali | 2005-11-21 15:54:11 |
 Megoldás a 79. feladatra:
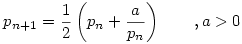
a.) eset: p0>0
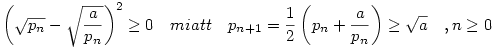
pn monoton fogyó, ugyanis n 1 esetén 1 esetén 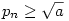 miatt miatt

Egy monoton fogyó alulról korlátos sorozatnak létezik határértéke, esetünkben az
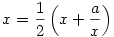
egyenlet pozitív gyöke. Ezért 
c.) eset: p0<0. ekkor pn monoton növő 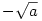 -hoz konvergáló sorozat. -hoz konvergáló sorozat.
b.) eset: p2005=? Tfh a>0 és 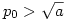 és legyen és legyen 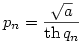 , ,
ahol 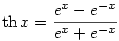
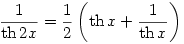 és a rekurzív összefüggés miatt és a rekurzív összefüggés miatt 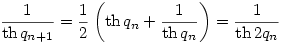
|
| Előzmény: [397] Lóczi Lajos, 2005-10-30 21:09:38 |
|
| [471] Lóczi Lajos | 2005-11-21 14:32:42 |
 Kíváncsi vagyok, hogy a matematikai programcsomagok hogyan reagálnának arra, ha megkérdeznék tőlük, mennyi a

összeg értéke. És szerintünk mennyi?
|
|
|
| [469] Lóczi Lajos | 2005-11-17 22:26:32 |
 Köszönöm az érdekes fejleményeket az ügyben (és hogy vetted a fáradságot bepötyögni a mátrixokat :)
(Én kb. 2000-ben foglalkoztam ezzel a kérdéssel (lám, azóta sokminden felkerült az internetre...) és emlékszem, többszáz CPU-órát használtam fel. A 40800 ezek szerint a 4x4-es maximum, én is azt sejtettem, most már beugrott a szám. Láttam, hogy a 7x7-es eset alsó becslésével Pfoertner több, mint 2 évet számolt :-) )
A legérdekesebb, hogy ezek szerint nem mindig akkor adódik a maximális determináns, ha a főátlóban vannak a legnagyobb elemek.
|
| Előzmény: [467] Róbert Gida, 2005-11-17 21:10:06 |
|
| [468] Róbert Gida | 2005-11-17 21:17:16 |
 93. feladat
Egy nxn-es komplex elemű mátrix determinánsának kifejtésénél azt a meglepő dolgot tapasztaltuk, hogy mind az n! tag valós része pozitív. Milyen n-re lehetséges ez?
|
|
| [467] Róbert Gida | 2005-11-17 21:10:06 |
 Legyen x(n) a maximális determináns az nxn-es mátrixok közt, melynek elemei pontosan az 1,2,..,n2 számok. Triviálisan x(1)=1 és x(2)=10 ( főátlóban 4 és 3 ). Megoldásom szerint x(3)=412 Ekkor Sloane adatbázisában az 1,10,412 sorozatra rákeresve egyetlen találatot ad, a miénket! Ez az A085000 sorozat: http://www.research.att.com/projects/OEIS?Anum=A085000 Még állítólag 3 tag ismert a sorozatból!
x(4)=40800, mátrixot nem ad meg hozzá.
x(5)=6839492 mátrixot is ad hozzá:

x(6)=1865999570 ehhez is ad mátrixot:

Alsó becslések ( Hugo Pfoertner ): x(7) 762140212575 és x(8) 762140212575 és x(8) 440857916120379, x(7)-re ez már jobb becslés, mint amit Sloane-nál találhatunk, ez a http://www.recmath.org-on található. Itt éppen a te problémád egy javasolt programozási versenyfeladat, hogy minnél jobb becslést találjunk x(n) sorozatra. Nagyon kevés nyílt programozási verseny van a weben, jó ha 2. Ezek közül az egyik a híres Al Zimmermann prog. verseny: évente van 3-4 feladat és nagyon nagy dolognak számít ezen nyerni. Jelenleg is tart egy verseny: cél az 1,2,3,...,n sugarú körök bepakolása egy minimális sugarú körbe, hogy a körök diszjunktak legyenek. Ez a feladat 5 440857916120379, x(7)-re ez már jobb becslés, mint amit Sloane-nál találhatunk, ez a http://www.recmath.org-on található. Itt éppen a te problémád egy javasolt programozási versenyfeladat, hogy minnél jobb becslést találjunk x(n) sorozatra. Nagyon kevés nyílt programozási verseny van a weben, jó ha 2. Ezek közül az egyik a híres Al Zimmermann prog. verseny: évente van 3-4 feladat és nagyon nagy dolognak számít ezen nyerni. Jelenleg is tart egy verseny: cél az 1,2,3,...,n sugarú körök bepakolása egy minimális sugarú körbe, hogy a körök diszjunktak legyenek. Ez a feladat 5 n n 50-re. 50-re.
|
| Előzmény: [464] Lóczi Lajos, 2005-11-17 19:10:22 |
|
| [466] Káli gúla | 2005-11-17 20:21:54 |
 Igazad van, bár csupa negatív tagnál felcserélhetnénk két sort, és akkor csupa pozitív tagot kapnánk.
Egy újj gyakorlat. 92. feladat. A két és háromdimenziós kockának van egy érdekes tulajdonsága: ha a csúcsokat valahogy két azonos elemszámú részre bontjuk (elfelezzük), akkor a két ponthalmaz egybevágó lesz. Megvan-e ez a tulajdonsága a négydimenziós kockának is?
|
| Előzmény: [462] Róbert Gida, 2005-11-17 18:24:53 |
|
| [465] Róbert Gida | 2005-11-17 19:15:26 |
 Megoldás a 90. feladatra:
Ha A egy nxn-es mátrix, melynek minden eleme +-1, akkor a mátrix determinánsa osztható 2n-1-gyel. Ez n=1-re trivi, indukcióval, ha n=k-ra igaz, akkor n=k+1-re is igaz. Induljunk a csupa 1 mátrixból, ennek sorai összefüggnek, így determinánsa nulla, egy-egy lépésben a mátrix egy elemét -1-re változtatva bármely mátrixot megkaphatunk. Egy lépésben a mátrix determinánsát kifejtve abban a sorban, ahol egy elemet megváltoztattunk: az eredeti determináns+-2*aldetermináns lesz az új determináns, de az aldetermináns az indukció miatt osztható 2k-2-vel, így a determináns 2k-1-gyel osztható marad. Ami kellett.
Ha n>1 akkor a 0 mindig lehet a determináns: legyen A csupa 1 mátrix. Elég pozitív determinánsokat előállítani, mivel a determináns előjelet vált, ha két oszlopát felcseréljük.
n=3-ra a determináns legfeljebb 6, mivel 6 darab kifejtési tag van. De a determináns osztható 4-gyel. Így csak -4,0,4 lehet, ezek közül mindegyik előáll, az előbbiek miatt elég 4-re előállítást mutatni: legyen
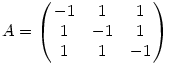
n=4-re 24 darab kifejtési tag van és a determináns osztható 8-cal, így csak -16,-8,0,8,16 lehet és mindegyik előáll, elég -8-ra és -16-ra példát mutatni: legyen
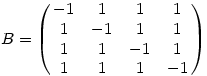
. Ekkor det(B)=-16 . Legyen

Ekkor det(C)=-8
|
|
| [464] Lóczi Lajos | 2005-11-17 19:10:22 |
 Régebben a 4x4-es analóg esetet is végigszámoltam, azzal a feltevéssel, hogy a főátlóban állnak a maximális elemek (tehát 16, 15, 14, 13). Aztán ha jól emlékszem valaki végigszámolta mindet és meghatároztuk a maximális elrendezést. Sajnos, nem látszott az általános minta. Milyen jó lenne látni pl. az 5x5-ös, stb. eseteket is... (tehát a mátrixot 1,2, ... , n2 számokkal feltöltve)
Aki ehhez hasonló problémákat akar keresgetni az interneten, az a Hadamard-féle maximális determinánsproblémára keressen pl. rá. Számos speciális alakú mátrix esetén ismert a maximum, de nem találtam eddig sehol eredményeket a fent feltett kérdésemre. Persze általánosabban is vizsgálható lenne a kérdés. Pl. egy ujjgyakorlat a következő:
Adott 4 valós szám. Mely elrendezés mellett lesz a belőlük képzett 2x2-es determináns abszolút értéke maximális?
|
| Előzmény: [463] Róbert Gida, 2005-11-17 18:41:47 |
|
| [463] Róbert Gida | 2005-11-17 18:41:47 |
 Megoldás a 89. feladatra:
A minimum egyszerű, legyen ugyanis:
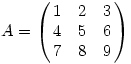
Ekkor A sorai lineárisan összefüggnek, így determinánsa nulla, így a minimum is nulla. A maximumra egy egyszerű program segítségével mind a 9! esetet végignézve ( persze lehetne kevesebbel is ), kapjuk, hogy a maximum 412 és ezt pl.

mátrixon vétetik fel. Egyébként nem véletlenül 412-öt is felveszi, mert ha -412 állna elő, akkor 2 oszlopát felcserélve a determináns ellentettjére vált.
|
|
| [462] Róbert Gida | 2005-11-17 18:24:53 |
 Valójában az indukció miatt az is kell, hogy pozítiv tag is van a kifejtési tagok közt. Amit persze ugyanúgy beláthatsz.
Megoldásom: n=3-ra szorozzuk össze a kifejtési tagokat, ekkor mivel a mátrix minden eleme két permutációban szerepel és a 6 féle permutáció közt 3 páros és 3 páratlan, ezért szorzatuk páratlan, így a kifejtési tagok szorzata 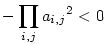 , de akkor a kifejtési tagok közt van pozitív és negatív is, ami kellett. , de akkor a kifejtési tagok közt van pozitív és negatív is, ami kellett.
|
| Előzmény: [456] Káli gúla, 2005-11-16 23:29:23 |
|




 n:=A-xn>0, akkor tehát A
n:=A-xn>0, akkor tehát A

 k+1 és
k+1 és 