| [565] HoA | 2009-08-31 08:50:46 |
 Attól tartok, az adott középpontú, adott parabolát érintő kör szerkesztése nem euklideszi feladat, így ennek sugara sem meglepő ha kívül esik a szerkeszthető szakaszok halmazán.
|
| Előzmény: [564] psbalint, 2009-08-29 16:21:43 |
|
| [564] psbalint | 2009-08-29 16:21:43 |
 sziasztok! egy rövid kérdésem lenne. elfelejtettem, hogy hogyan számoljuk ki egy pont és egy parabola távolságát. illetve hát sejtem, hogy melyik egyenesnek kell melyikre merőlegesen állnia, de mindig harmadfokú egyenlet jön ki a végén. segítsééég!
|
|
|
| [562] jonas | 2009-07-15 13:38:40 |
 Kis egészeken próbálgatással azt kapjuk, hogy az a=b=c=2 az egyetlen megoldás. Nagy számokra nem lehet megoldás, mert a faktoriális monoton, így ha valamelyik szám nagy, akkor a d is nagy, de akkor a,b,c d-1 csakhogy ebből a!,b!,c! d-1 csakhogy ebből a!,b!,c! (d-1)!<d!/3 így a!+b!+c!<d! ami ellentmondás. (d-1)!<d!/3 így a!+b!+c!<d! ami ellentmondás.
|
| Előzmény: [561] MTM, 2009-07-15 11:06:14 |
|
| [561] MTM | 2009-07-15 11:06:14 |
 Oldjuk meg a poz. egészek halmazán!
a!+b!+c!=d!
|
|
|
|
| [558] Csimby | 2009-04-07 02:18:32 |
 F(x,y) az (x,y) pont távolságainak összege a (-1,1),(1,-1),(-2,-2) pontoktól. Ismert, hogy ez a három pont által meghatározott háromszög izogonális pontjában minimális, melyet megszerkeszthetünk ha az oldalakra kifelé írt szabályos háromszögek megfelelő csúcsát összekötjök az eredeti háromszög megfelelő csúcsával. Ezek alapján a keresett pont az x=y egyenesen lesz. És mivel az izogonális pontból az oldalak 120° szögben látszanak, azt is könnyű látni, hogy a keresett pont: 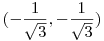 . .
|
| Előzmény: [557] Cogito, 2009-04-05 15:20:06 |
|
| [557] Cogito | 2009-04-05 15:20:06 |
 108.feladat: 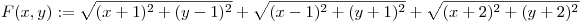 , ahol x és y tetszőleges valós számok. Keressük meg F lehető legkisebb értékét. , ahol x és y tetszőleges valós számok. Keressük meg F lehető legkisebb értékét.
|
|
| [556] MTM | 2008-11-24 21:20:23 |
 Üdv!
Határozzuk meg
a, x4-4x3+1 és x3-3x2+1
b, 3x6-x5-9x4-14x3-11x2-3x-1 és 3x5+8x4+9x3+15x2+10x+9
polinomok legnagyobb közös osztóját.
|
|
|
|
|
| [552] Lóczi Lajos | 2008-10-29 01:34:00 |
 Most már egyszerűen megoldható az alábbi 106'. példa.
Legyen adott az f valós függvény, amely mindenhol differenciálható. Adjunk meg olyan g és h mindenhol értelmezett, de sehol sem deriválható valós függvényeket, amelyekre fennáll, hogy f=g.sin+h.cos.
|
| Előzmény: [546] Suhanc, 2008-10-27 18:50:49 |
|
|
|
|
|
|
| [546] Suhanc | 2008-10-27 18:50:49 |
 Hallottam valakitől, aki hallotta valakitől, aki olvasta valahol...és mindegyikünknek tetszett:
106.Feladat: Igazoljuk, hogy tetszőleges f folytonos fv-hez léteznek g,h folytonos fv-ek, melyekkel f "harmonikus felbontását" nyerjük, értsd: f(x)=g*sin (x)+h*cos (x)
|
|
| [545] Sirpi | 2008-10-17 10:20:30 |
 Először elfilóztam rajta pár másodpercig, hogy mégis mi lehet a csavar a feladatban, aztán elolvastam a topik címét, és rájöttem, hogy nem kell túl bonyolultra gondolnom :-)
De nyitva hagyom a feladatot, és egy egyszerű helyett egy érdekesebb megoldást írok rá (szóval ha van egyszerű megoldása valakinek, írja be nyugodtan :-) ). Szóval legyen mondjuk
105. a) feladat: Biz. be, hogy az an= (n)/n sorozat jó, ahol (n)/n sorozat jó, ahol  az Euler-féle (számelméleti) fi-függvény. az Euler-féle (számelméleti) fi-függvény.
|
| Előzmény: [544] Csimby, 2008-10-16 17:47:38 |
|
| [544] Csimby | 2008-10-16 17:47:38 |
 Így van. Itt egy újabb feladat:
105.feladat Adjunk meg olyan sorozatot, melynek a [0,1] intervallum minden eleme torlódásipontja. (akkor mondjuk, hogy egy pont a sorozat torlódási pontja, ha bármilyen kicsi környezetébe a sorozatnak végtelen sok tagja esik)
|
| Előzmény: [543] m2mm, 2008-09-26 22:16:08 |
|
| [543] m2mm | 2008-09-26 22:16:08 |
 Üdv!
2 szelvény még nyilván nem elég(mert lehet, hogy egyik tipp sem jön be), de 3 már elég: egyik szelvényen minden tipp legyen 1, a másodikon mindegyik 2, a harmadikon mindegyik X. Ekkor minden meccsre mindhárom tippet adtunk, ezért minden meccset eltalálunk pontosan egyszer, tehát a 3 szelvényen 13 helyes tipp van. Ha nem lenne egyik szelvényen sem legalább 5 találat, akkor maximum 4 lehet mindegyiken, így összesen 12 helyes tipp lehetne, ami kisebb, mint 13 (amennyi helyes tipp van valójában). Azaz az egyik szelvény legalább 5 találatos.
|
| Előzmény: [540] Csimby, 2008-09-25 17:05:07 |
|
|
|





 d-1 csakhogy ebből a!,b!,c!
d-1 csakhogy ebből a!,b!,c!




 k)=f(2
k)=f(2
 (n)/n sorozat jó, ahol
(n)/n sorozat jó, ahol