|
| [635] BohnerGéza | 2010-08-23 21:03:07 |
 Ha a csomó a lyukhoz ér, megáll. Egy súly nem emeli föl a másikat, hisz egyenlők. Addig történhet mozgás, míg a harmadik súly rásegít, de ez véget ér, ha a csomó a lyukhoz ér.
Érdemes helyzeti energia szempontjából is vizsgálni a feladatot:
Akkor áll meg a súlyok mozgása (persze, ha csillapodás is van), ha az összes helyzeti energiájuk a legkisebb, azaz az asztal fölött a madzagok összhossza a legkisebb. Tehát azt a pontot keressük, melyre a tőle a csúcsokig tartó szakaszok összege minimális.
Ez az olyan háromszögeknél, melyek minden szöge kisebb 120 foknál, valóban az izogonális pont. Az olyan háromszögeknél, melynek van legalább 120 fokos szöge, ennek csúcsa.
|
| Előzmény: [633] SmallPotato, 2010-08-22 14:39:35 |
|
|
| [633] SmallPotato | 2010-08-22 14:39:35 |
 A jelzett esetben valóban nem állhat elő a három egyforma szög; ebből adódóan viszont ekkor a három egyenlő nagyságú erő nem tarthat egyensúlyt. Konkrétan az fog történni, hogy a 120 fokot elérő szögnél levő lyukba az ott lévő súly berántja a csomót és a rendszert csak valamelyik másik súly elakadása állítja meg.
Olyasmi helyzet ez, mint az utca két oldala között kifeszített tartókábel és az azon, (az egyszerűség kedvéért most középen) lógó lámpa. Ha a tartókábel túl feszes (azaz két ága az egyenesszöghöz közeli szöget zár be), a felfüggesztésben lényegesen nagyobb erők ébrednek, mint a lámpa súlya. Konkrétan ha a tartókábel ágai 120 foknál többet zárnak be, akkor a bennük ébredő erő a lámpa súlyánál nagyobb kell hogy legyen; vagy megfordítva: ha a feszítőerőnek nem szabad meghaladnia a lámpa súlyát, akkor a szög nem haladhatja meg a 120 fokot.
|
| Előzmény: [631] gubanc, 2010-08-22 12:03:56 |
|
| [632] bily71 | 2010-08-22 14:12:35 |
 1Ft=100f=10f*10f=1/10Ft*1/10Ft=1/100Ft=1f, vagyis 1 forint=1 fillér.
Hol a hiba?
|
|
| [631] gubanc | 2010-08-22 12:03:56 |
 Ezt a példát már én is hallottam, de diszkussziós választ még nem. A feladat tetszőleges háromszögről szól. Kós Géza a GEOMETRIA [268]-ban ezt írja: „Ha valamelyik szög éppen 120 fok vagy annál nagyobb, akkor nincs izogonális pont”. Ha ez igaz, hol lesz a csomó az ilyen háromszögeknél és mi a teljes indoklás?
|
| Előzmény: [630] Fernando, 2010-08-22 08:39:22 |
|
| [630] Fernando | 2010-08-22 08:39:22 |
 Szerintem ez az ún. izogonális pont, ahonnan a háromszög három oldala azonos szög alatt látszik = a csúcsokhoz vezető szakaszok hosszösszege minimális.
|
|
|
|
|
| [626] sakkmath | 2010-08-21 22:30:19 |
 Rajzoljunk egy asztal lapjára tetszőleges háromszöget. Csúcsaiban fúrjunk egy-egy lyukat az asztalba. Fűzzünk át a lyukakon egy-egy cérnát és kössünk azok alsó végeire egy-egy súlyt. A cérnaszálak felső végeit az asztallap fölött csomózzuk össze, aztán hagyjuk, hogy a lógó súlyok a cérnaszálakat megfeszítsék. (Feltesszük, hogy a cérnák nem szakadnak el.)
Hol lesz a csomó egyensúlyi helyzete, ha a három súly egyenlő?
|
|
|
|
|
|
|
|
| [619] Fernando | 2010-04-13 11:20:38 |
 Mennyi a valószínűsége, hogy a lottón kihúzott számok között nincsenek szomszédosak?
|
|
|
| [617] Lóczi Lajos | 2010-04-07 15:45:30 |
 (Nem jól mondtam: az optimalitás bizonyításához mindkét oldalon arra volt szükségem, hogy az n(e-(1+1/n)n) függvény monoton növő és limesze a végtelenben micsoda. Viszont a monotonitás nem jött ki 1-2 sorban.)
|
| Előzmény: [616] Lóczi Lajos, 2010-04-07 15:20:27 |
|
| [616] Lóczi Lajos | 2010-04-07 15:20:27 |
 Valóban, tehát az optimális konstansok a kétoldali becslésben az e-2, illetve az e/2; azaz minden n pozitív egészre
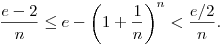
Az e/2 egyszerűen kijön, de Neked milyen technikával jött ki az e-2 (mert nekem csak kicsit körülményesen, monotonitási érveléssel)?
|
| Előzmény: [615] nadorp, 2010-04-07 11:19:07 |
|
|
|
| [613] HoA | 2010-03-30 11:48:16 |
 Ne kötözködj, még a végén kiderül, hogy a "prím"-ség, sőt az "egész"-ség sem feltétel. A 2010 helyetti tetszőleges nemnulla egészről nem is beszélve :-)
|
| Előzmény: [611] BohnerGéza, 2010-03-29 18:18:07 |
|
|












