| [665] Róbert Gida | 2011-09-25 14:00:46 |
 Ügyes vagy, leülhetsz. Az azért látható, hogy csak néhány kisebb/nagyobb egyenlőt szúrtam el. Helyesen:
Ebben az esetben  esetében a kolónia fennmaradhat, míg esetében a kolónia fennmaradhat, míg 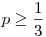 esetén biztosan kipusztul. Legyen először esetén biztosan kipusztul. Legyen először 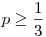 , ha legfeljebb , ha legfeljebb  sárkányfiú van, akkor első hadjárat során öljék meg őket, ekkor nem marad sárkányfiú, és a kolónia kihal. Így feltehető, hogy több, mint sárkányfiú van, akkor első hadjárat során öljék meg őket, ekkor nem marad sárkányfiú, és a kolónia kihal. Így feltehető, hogy több, mint  sárkányfiú van, ami azt jelenti, hogy kevesebb, mint sárkányfiú van, ami azt jelenti, hogy kevesebb, mint 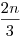 sárkánylány. Ekkor a hadjáratok során csak őket öljék meg: legyen kezdetben sárkánylány. Ekkor a hadjáratok során csak őket öljék meg: legyen kezdetben 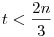 sárkánylány a kolóniában, ekkor egy hadjárat után számuk t-pn lesz (vagy nulla, ha ez negatív), míg a szülések után 2(t-pn)<t, így n év alatt kihalnak. sárkánylány a kolóniában, ekkor egy hadjárat után számuk t-pn lesz (vagy nulla, ha ez negatív), míg a szülések után 2(t-pn)<t, így n év alatt kihalnak.
Ellenkező irány: legyen  és és  sárkányfiú és sárkányfiú és 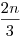 sárkánylány. Egy hadjárat alatt megölnek kevesebb, mint sárkánylány. Egy hadjárat alatt megölnek kevesebb, mint  sárkányt, így biztosan megmarad legalább sárkányt, így biztosan megmarad legalább  sárkánylány és legalább egy sárkányfiú. A szülésekkel pótolják a meghalt sárkányokat (annyi sárkánylány és fiú szülessen, mint amennyit megöltek), ekkor visszaáll az eredeti állapot, a maradék születések olyanok legyenek, hogy a kolóniában az 1:2 arány fennmaradjon a sárkányfiúk és lányok között (+-1 sárkány, ha n nem osztható 3-mal). Ekkor a kolónia nem hal ki, feltéve, hogy n elég nagy. Ezt csak Kemény Legénynek írom, mert igen, ha mondjuk p=0.3333, akkor bizony megeshet, hogy mondjuk az ezredik hadjárat után szépen kihalnak (ha a kezdeti n kicsi, és a +-1 sárkány éppen annyira megbillenti az 1:2 arányt, hogy nekünk rossz lesz). sárkánylány és legalább egy sárkányfiú. A szülésekkel pótolják a meghalt sárkányokat (annyi sárkánylány és fiú szülessen, mint amennyit megöltek), ekkor visszaáll az eredeti állapot, a maradék születések olyanok legyenek, hogy a kolóniában az 1:2 arány fennmaradjon a sárkányfiúk és lányok között (+-1 sárkány, ha n nem osztható 3-mal). Ekkor a kolónia nem hal ki, feltéve, hogy n elég nagy. Ezt csak Kemény Legénynek írom, mert igen, ha mondjuk p=0.3333, akkor bizony megeshet, hogy mondjuk az ezredik hadjárat után szépen kihalnak (ha a kezdeti n kicsi, és a +-1 sárkány éppen annyira megbillenti az 1:2 arányt, hogy nekünk rossz lesz).
|
| Előzmény: [664] Kemény Legény, 2011-09-25 11:36:54 |
|
| [664] Kemény Legény | 2011-09-25 11:36:54 |
 Tehát az ellenkező irányra adott megoldásod pl. az n=6, 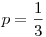 esetben: van 2 sárkányfiú+ 4 sárkánylány. Ha Artúr megöli mind a 2=n*p sárkányfiút, a lányok nehezen fognak utódokat nemzeni és pótolni a veszteségeket... esetben: van 2 sárkányfiú+ 4 sárkánylány. Ha Artúr megöli mind a 2=n*p sárkányfiút, a lányok nehezen fognak utódokat nemzeni és pótolni a veszteségeket...
|
| Előzmény: [663] Róbert Gida, 2011-09-25 09:40:53 |
|
| [663] Róbert Gida | 2011-09-25 09:40:53 |
 Ebben az esetben  esetében a kolónia fennmaradhat, míg esetében a kolónia fennmaradhat, míg 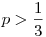 esetén biztosan kipusztul. Legyen először esetén biztosan kipusztul. Legyen először 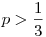 , ha legfeljebb , ha legfeljebb  sárkányfiú van, akkor első hadjárat során öljék meg őket, ekkor nem marad sárkányfiú, és a kolónia kihal. Így feltehető, hogy legalább sárkányfiú van, akkor első hadjárat során öljék meg őket, ekkor nem marad sárkányfiú, és a kolónia kihal. Így feltehető, hogy legalább  sárkányfiú van, ami azt jelenti, hogy legfeljebb sárkányfiú van, ami azt jelenti, hogy legfeljebb 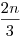 sárkánylány. Ekkor a hadjáratok során csak őket öljék meg: egy hadjárat után számuk kevesebb, mint sárkánylány. Ekkor a hadjáratok során csak őket öljék meg: egy hadjárat után számuk kevesebb, mint  lesz, míg a szülések után kevesebb, mint lesz, míg a szülések után kevesebb, mint  , így , így 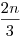 év alatt kihalnak. év alatt kihalnak.
Ellenkező irány: legyen  és és  sárkányfiú és sárkányfiú és 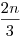 sárkánylány. Egy hadjárat alatt megölnek legfeljebb sárkánylány. Egy hadjárat alatt megölnek legfeljebb  sárkányt, így biztosan megmarad legalább sárkányt, így biztosan megmarad legalább  sárkánylány. A szülésekkel pótolják a meghalt sárkányokat (annyi sárkánylány és fiú szülessen, mint amennyit megöltek), ekkor visszaáll az eredeti állapot, a maradék születések olyanok legyenek, hogy a kolóniában az 1:2 arány fennmaradjon a sárkányfiúk és lányok között (+-1 sárkány, ha n nem osztható 3-mal). Ekkor a kolónia nem hal ki sárkánylány. A szülésekkel pótolják a meghalt sárkányokat (annyi sárkánylány és fiú szülessen, mint amennyit megöltek), ekkor visszaáll az eredeti állapot, a maradék születések olyanok legyenek, hogy a kolóniában az 1:2 arány fennmaradjon a sárkányfiúk és lányok között (+-1 sárkány, ha n nem osztható 3-mal). Ekkor a kolónia nem hal ki
|
| Előzmény: [662] Csimby, 2011-09-24 19:27:09 |
|
| [662] Csimby | 2011-09-24 19:27:09 |
 Ez jó, ha véletlenszerűen ölik a sárkányokat. De most engedjük meg, hogy válogathassanak is (valami külső jel alapján el tudják dönteni egy alvó sárkányról hogy hím vagy nőstény).
|
| Előzmény: [661] Róbert Gida, 2011-09-24 19:14:02 |
|
| [661] Róbert Gida | 2011-09-24 19:14:02 |
 Aha, akkor q=2 (azaz 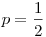 ) a megoldás. Hiszen először legyen ) a megoldás. Hiszen először legyen 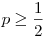 , vagy nem marad sárkányfiú egy hadjárat után, így nincs születés, és a kolónia kihal egy mértani sor szerint. Ha van sárkányfiú, akkor a hadjárat után legfeljebb , vagy nem marad sárkányfiú egy hadjárat után, így nincs születés, és a kolónia kihal egy mértani sor szerint. Ha van sárkányfiú, akkor a hadjárat után legfeljebb 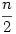 sárkány marad, (legalább) egyikük sárkányfiú, így legfeljebb sárkány marad, (legalább) egyikük sárkányfiú, így legfeljebb 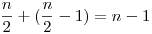 -en lesznek a hadjárat és a szülések után. Így n év alatt kihalnak. -en lesznek a hadjárat és a szülések után. Így n év alatt kihalnak.
Ha 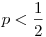 , akkor adható olyan n, amelyre a kolónia létszáma egy r>1 kvóciensű mértani sorozattal becsülhető alulról, így nem hal ki. (kezdetben egy sárkányfiú legyen a kolóniában, őt egy hadjárat során se öljék meg, és mindig sárkánylány szülessen.) , akkor adható olyan n, amelyre a kolónia létszáma egy r>1 kvóciensű mértani sorozattal becsülhető alulról, így nem hal ki. (kezdetben egy sárkányfiú legyen a kolóniában, őt egy hadjárat során se öljék meg, és mindig sárkánylány szülessen.)
|
| Előzmény: [660] Csimby, 2011-09-24 17:03:01 |
|
| [660] Csimby | 2011-09-24 17:03:01 |
 n-sárkányból legfeljebb 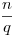 felsőegészrésznyit tud megölni. És a legnagyobb olyan q-t keressük amivel végezni tud velük. (Örök élet = végelgyengülésben nem hal meg. De ha levágják a fejét, akkor persze igen.) felsőegészrésznyit tud megölni. És a legnagyobb olyan q-t keressük amivel végezni tud velük. (Örök élet = végelgyengülésben nem hal meg. De ha levágják a fejét, akkor persze igen.)
|
| Előzmény: [658] Róbert Gida, 2011-09-24 10:56:30 |
|
|
| [658] Róbert Gida | 2011-09-24 10:56:30 |
 "Nyilván olyan p kell ami a "legrosszabb esetben" is működik." Nem nyilvánvaló.
"Példádban, ha örök életűek a sárkányfiúk akkor nem jó a p=0, mert Artúr egyet se öl meg, ők meg nem döglenek meg maguktól" De, akkor p>0 esetben egy örök életű sárkányt hogyan lehet megölni? Mert akkor az a sárkány nem örök életű.
Feladatodnak akkor viszont nincs megoldása: tegyük fel n>1 a kolónia létszáma kezdetben. Ha ennek p-ed részét ölik meg, akkor 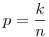 (0 (0 k k n egész), mivel ennek minden n>1-re müködnie kell így csak p=0 és p=1 lehet. De az előbbi nem megoldás szerinted. Míg p=1 sem lehet, mert: "p-ed részét sikerül legyilkolnia mielőtt felébrednek és elkergetik.", de akkor egy sárkány sem marad, így nem kergethette el őket senki. n egész), mivel ennek minden n>1-re müködnie kell így csak p=0 és p=1 lehet. De az előbbi nem megoldás szerinted. Míg p=1 sem lehet, mert: "p-ed részét sikerül legyilkolnia mielőtt felébrednek és elkergetik.", de akkor egy sárkány sem marad, így nem kergethette el őket senki.
|
|
| [657] Csimby | 2011-09-24 00:02:38 |
 Példádban, ha örök életűek a sárkányfiúk akkor nem jó a p=0, mert Artúr egyet se öl meg, ők meg nem döglenek meg maguktól. Nyilván olyan p kell ami a "legrosszabb esetben" is működik.
|
| Előzmény: [656] Róbert Gida, 2011-09-23 20:26:08 |
|
|
| [655] Csimby | 2011-09-23 18:52:48 |
 Artúr király minden télen hadjáratot indít a hegyekben élő sárkányok ellen, akik ilyenkor téli álmunkat alusszák barlangjukban. A barlangban talált jószágok p-ed részét sikerül legyilkolnia mielőtt felébrednek és elkergetik. Párzási időszak után minden sárkánylány kis sárkánynak ad életet (egészen addig amíg a kolóniában van fiú sárkány). A kis sárkányok, hála a mágikus környezetnek, már a következő párzási időszakra nemzőképesek lesznek. Mi a legkisebb p, amilyen hatékonysággal Artúr ki tudja irtani a sárkány kolóniát?
|
|
| [654] jonas | 2011-09-06 21:09:49 |
 A következő feladatot sokat ismerhetitek. Nem emlékszem, szerepelt-e már a fórumon.
Lássuk be, hogy a következő sorozat tagjai páronként relatív prímek.
3,5,17,257,65537,4294967297,...,22n+1,...
|
|
| [653] Valezius | 2011-04-12 14:38:15 |
 Egy 2nx2n méretű négyzetrácsos ábrába hurkot rajzolunk olyan módon, hogy a hurok minden négyzeten átmegy, és mindig oldalasan szomszédos mezők középpontjait köti össze. (Egyszerűbben mondva csak vízszintesen és függőlegesen mehetünk)
Az egyik helyre, ahol a hurok irányt vált (például az egyik sarokba) rajzolunk egy kört, majd a hurkon végighaladva minden második töréspontra (és csak azokra) újabb kört rajzolunk.
1. Lássuk be, hogy a 4 sarok közül pontosan két szemben lévőben lesz kör.
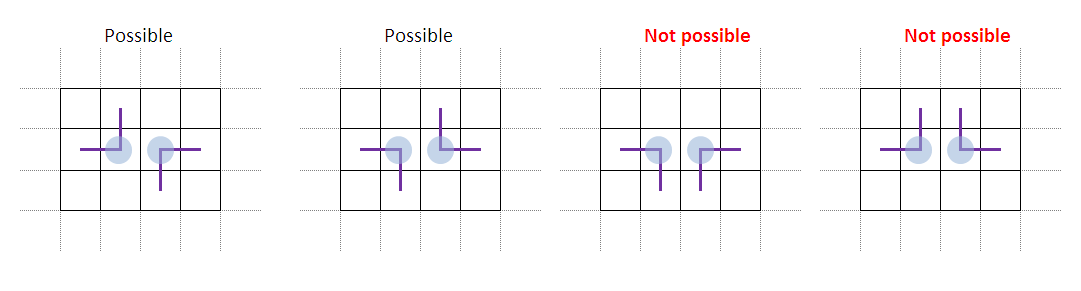
2. Ha két kör egymás mellett van, akkor a képen látható négy lehetőség közül csak az első kettő valósulhat meg.
Mindkét bizonyítást elég egyszerűnek gondolom, úgyhogy remélem jó helyen van az ujjgyakorlatok között.
A könnyebb érthetőség kedvéért itt van néhány logikai feladvány, ahol minden kör meg van adva, és a feladat a hurok megrajzolása. www.logikairejtveny.5mp.eu
|
 |
|
|
|
| [650] bily71 | 2010-09-01 21:36:23 |
 Legyen a=b+c !
Ekkor:
5a=5b+5c
4b+4c=4a
Adjuk össze a két egyenletet!
5a+4b+4c=5b+5c+4a
Mindkét oldalból vonjunk ki 9a-t!
4b+4c-4a=5b+5c-5a
Ebből:
4(b+c-a)=5(b+c-a)
Vagyis 4=5. Hol a hiba?
|
|
|
| [648] jenei.attila | 2010-08-31 16:00:59 |
 Ne haragudj Bily, de a kérdést nem átfogalmaztad, hanem egyszerűen mást kérdezel. A négyzetmentes számokra igaz, hogy nem hatványszámok, de fordídva nem. A kezdőtagok nevezőiben pedig as szerepel, akármi is az a. Tehát az eredeti kérdésedben, ahol azt mondtad hogy az a négyzetmentes, nem fog szerepelni a 12s, mivel a 12 nem négyzetmentes. Ha most azt mondod, hogy az a mégis inkább legyen nem hatványszám, akkor szerepelni fog benne, mivel a 12 valóban nem hatványszám. Előbb döntsd el hogy mit kérdezel, és ne tegyél úgy mintha én lennék értetlen hülye! Legalább annyit írhattál volna, hogy bocsi, rosszul tettem fel a kérdést. Még hogy átfogalmaztad... Most felbosszantottál.
|
| Előzmény: [646] bily71, 2010-08-31 14:23:52 |
|
| [647] SAMBUCA | 2010-08-31 15:24:20 |
 Egyszerűen megválaszolható, ujjgyakorlat :) két dolgot kell ellenőrízni:
a, minden 1/ns szerepel a jobboldalon
b, egyik sem szerepel kétszer.
Sambuca
|
| Előzmény: [646] bily71, 2010-08-31 14:23:52 |
|
| [646] bily71 | 2010-08-31 14:23:52 |
 Szerintem meg a kezdőtagok nevezőiben az a számok azok a pozitiv egészek, amelyek nem állnak elő a=br alakban, ahol b és r pozitiv egészek és r>1, azaz bármely 1-nél nagyobb r esetén a r-edik gyöke nem egész szám.
Az 1/12s úgy lesz kezdőtag, hogy nem szerepel egyik előző sorban sem, vagyis igy:
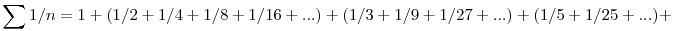
+(1/6+1/36+...)+(1/7+1/49+...)+(1/10+1/100+...)+(1/11+1/121+...)+(1/12+1/144+...)+...
Tehát a kérdésem átfogalmazva:
Igaz-e, hogy
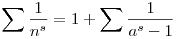
ahol a befutja a nem hatványszámokat, n pedig a pozitiv egészeket?
|
| Előzmény: [645] jenei.attila, 2010-08-31 08:53:06 |
|
| [645] jenei.attila | 2010-08-31 08:53:06 |
 Sajnos nem értem mire gondolsz: "csakhogy a kezdőtagok nevezőjében lévő a-k, mint ahogy az ellenpéldád is mutatja (az 1/12s is kezdőtag), nem azonosak a négyzetmentes számokkal"
Szerintem a kezdőtagok nevezői éppen a négyzetmentes számok. Továbbra sem találom az 1/12s-ent. Ez szerinted hogyan lesz kezdőtag? A következő hozzászólásodban az r mit jelent? Mi az, hogy az r-edik gyök nem egész szám? Létezik ilyen r, vagy minden r-re? Légyszíves próbáld ezt világosabban kifejteni. Köszi.
|
| Előzmény: [643] bily71, 2010-08-30 22:33:35 |
|
|
| [643] bily71 | 2010-08-30 22:33:35 |
 s=1 esetén:
1/1+1/2+1/3+...=1+(1/2+1/4+1/8...)+(1/3+1/9+1/27+...)+(1/5+1/25+1/125+)+...
s=2 esetén:
1/1+1/4+1/9+...=1+(1/4+1/16+1/64+...)+(1/9+1/81+1/729+...)+(1/25+1/625+1/15625+...)+...
...
A zárójelekben olyan mértani sorok vannak, melyek kezdőtagjai nem szerepeltek egyik elöző zárójelben sem és a kezdőtag egyenlő a kvócienssel, csakhogy a kezdőtagok nevezőjében lévő a-k, mint ahogy az ellenpéldád is mutatja (az 1/12s is kezdőtag), nem azonosak a négyzetmentes számokkal, ezen számok halmaza bővebb.
|
| Előzmény: [641] jenei.attila, 2010-08-30 12:23:13 |
|
|
|






 k
k





 N és r>1 esetén nem egész szám.
N és r>1 esetén nem egész szám.