|
| [685] patba | 2011-11-29 16:36:48 |
 Értettem a feladatot, de az FBI nem 9 pontos ujjlenyomatot tárol/használ, hanem 12 pontost. Ekkor 1:1,25.1020 az esélye annak, hogy két különböző ember ujjlenyomata megegyezzen, legalábbis Osterburg szerint. Így viszont már hihető, hogy a 200 millió között nincs két egyforma.
|
| Előzmény: [683] Kemény Legény, 2011-11-29 09:37:24 |
|
|
| [683] Kemény Legény | 2011-11-29 09:37:24 |
 Róbert Gida kérdése szerintem arra utal, hogy ha egy N=64milliárd elemű halmazból visszatevéssel kiveszel k=200millió elemet, akkor annak igen kicsi az esélye, hogy ne legyen köztük 2 egyforma.
Képlettel: annak az esélye, hogy mind különböző:
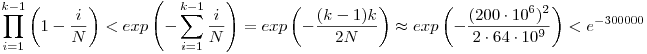
ami egy egészen kis szám, ezért nagyon valószínű, hogy van egyezés a 200millió adat között.
|
| Előzmény: [682] patba, 2011-11-28 22:23:46 |
|
|
| [681] Róbert Gida | 2011-11-28 21:11:29 |
 Egy valódi ujjgyakorlat: Kékfény szerint 9 pontot vizsgáva az ujjon 1 a 64 milliárdhoz annak az esélye, hogy valamely 2 ujjnyom megegyezzen. Elmúlt száz évben nem bukkantak 2 egyforma ujjlenyomatra ((2 különböző embertől)), pedig például az FBI-nál 200 millió ujjlenyomat van.
Mennyire higgyünk a Kékfénynek?
|
|
| [680] kovátsnorbi1994 | 2011-11-12 21:56:45 |
 Helló mindenkinek! Éppen egy hónapja érdeklődtem egy feladatsorral (ill. annak első részével) kapcsolatban, és profi válaszokat is kaptam kérdéseimre - a feladatokat végülis sikerült megoldanom az általatok megadott segítségek felhasználásával (hozzászólásom végén vázlatosan le is írom mire jutottam azokkal), már amennyire emlékszem belőle így néhány hét távlatából... Sajnos azóta elég kevés időm jutott PC elé ülni, így most onnan folytatom, ahol abbahagytam, vagyis a második feladatsorra kérdezek rá: (ezek közül leginkább a II. feladat példáihoz várnék ötleteket, megoldásokat, ott ugyanis elindulni sem tudok, én csak polinomosztással tudnék neki kezdeni, de azt tiltja a feladat...)
* * *
I. Ábrázolja vázlatosan a következő implicit alakban megadott függvényeket:
a.) x+sinx+2x=y+siny+2y b.) sinx=cosy c.) xy=yx 0<x,y
- - -
II. A következő feladatokban a polinom-osztás használatát mellőzzük (ellenőrzésre természetesen használhatjuk) !
a.) Az osztás elvégzése nélkül állapítsa meg a maradékot:
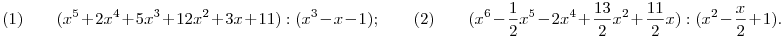
b.) Bontsuk tényezők szorzatára a következő kifejezéseket:
(1) x4+y4–xy(x3+y3)+xy(x2+y2)–8(x+y)+8xy-1 (2) 3xyz+x(y2+z2)+y(z2+x2)+z(x2+y2).
c.) A számláló és nevező átalakításával egyszerűsítsük az alábbi törteket:
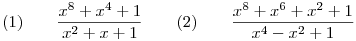
- - -
III. Mutassa meg, hogy
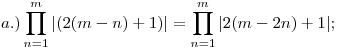

* * *
(Az első feladatsornál az eredményeim tehát:az 1. feladatban a határértékek, ahol léteztek vagyis az a) és c) feladat esetén is, azonosan 1-re adódtak, a 3. feladatban F ' (x)=mF(x)=f(x) ez utóbbi pedig (vagyis a kérdezett primitív függvény meredekségét) éppen a feladatban megadott (derivált)függvény helyettesítési értéke határozta meg az adott helyen, elvégezve a behelyettesítést 0 meredekséget kaptam. A 4. feladatnak (jonas hozzászólását tovább gondolva) minden x-re a=1 és ha b=0 akkor azonosságot kaptam, ami éppen eleget tett a feladat feltételeinek.)
|
| Előzmény: [679] jonas, 2011-10-15 21:03:20 |
|
| [679] jonas | 2011-10-15 21:03:20 |
 Nekem tetszenek ezek a gyakorlófeladatok, és a második adagra is kíváncsi vagyok, de azért jó lenne, ha azt is megosztanád velünk, hogy Te mire jutottál a feladatokkal a tippjeink után. Ha még mindig el vagy akadva valamelyikkel, akkor mondd meg hol.
|
| Előzmény: [676] kovátsnorbi1994, 2011-10-14 20:16:41 |
|
|
|
| [676] kovátsnorbi1994 | 2011-10-14 20:16:41 |
 Köszönöm mindenkinek aki válaszolt, hasznos és használható ötleteket kaptam, nem hiába írtam. Most nem sok időm van, de legközelebb a második - számomra problémás - feladatokat is megosztom veletek. Mégegyszer köszönöm a válaszokat és jó hétvégét Mindenkinek!
|
|
| [675] Fálesz Mihály | 2011-10-14 14:20:18 |
 Néhány gyakori ötlet, amit érdemes megjegyezni:
1. Sorozat határértéke helyett megpróbálhatod függvény határértékét venni: n vagy 1/n helyett x-et írsz. Függvényekre többféle eszközt használhatsz, mint sorozatokra, pl. a L'Hospital-szabályt.
2. Hatványok és gyökök helyett átírhatod a kifejezést törtekkel vagy szorzatokkal, ha veszed a logaritmusát. A végén majd behelyettesítesz az exponenciális függvénybe, ami folytonos.
Pl. az 1a feladatban megkeresheted a
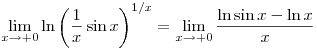
határértéket. (L'Hospital, rendezés, nagy levegő, még kétszer L'Hospital...)
|
| Előzmény: [674] Maga Péter, 2011-10-13 12:18:15 |
|
| [674] Maga Péter | 2011-10-13 12:18:15 |
 Az 1.-re (ha jól látom, ez maradt nyitva): az a) és c) feladatban használhatod a sin Taylor-sorból adódó közelítését a 0 pontban: 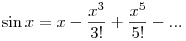 , az a)-ban valami olyasmi marad, hogy , az a)-ban valami olyasmi marad, hogy 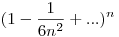 , csendőr-elvvel vagy Bernoulli-egyenlőtlenséggel is be tudod fejezni; a c)-ben hasonló módon. , csendőr-elvvel vagy Bernoulli-egyenlőtlenséggel is be tudod fejezni; a c)-ben hasonló módon.
A b)-ben van egy csomó nem értelmezett függvényérték: ahol a sin negatív, ott negatív számból kellene gyököt venni. A pozitív sin x-et adó részre szorítkozva sincs határérték, 0-hoz és 1-hez is tetszőlegesen közel kerülünk tetszőlegesen messze is.
|
| Előzmény: [669] kovátsnorbi1994, 2011-10-12 20:39:44 |
|
| [673] jonas | 2011-10-12 23:52:39 |
 A 2. feladathoz a következő kiírást tudom elképzelni, ha a megoldás 63 kell legyen.
Hány olyan permutációja van az (1,2,3,4,5,6) számoknak, amiben van valahol három szomszédos helyen három szomszédos szám növekvő sorrendben, de sehol nincs négy szomszédos helyen négy szomszédos szám növekvő sorrendben?
A 63 ilyen permutáció a következő: 123546 123564 123645 123654 124563 126345 132456 134526 145623 145632 152346 156234 163452 165234 214563 216345 231456 234156 234165 234615 234651 245613 245631 261345 263451 312456 314562 321456 324561 345126 345162 345216 345261 412356 412365 451236 456123 456132 456213 456231 456312 456321 461235 465123 512364 516234 523416 523461 541236 546123 562341 564123 612354 613452 615234 621345 623415 634512 634521 641235 645123 652341 654123 .
Az 1. feladathoz most inkább nem szólok hozzá, mert fáradt vagyok, hanem megvárom, hogy valaki olyan segítsen, aki jobban ért az analízishez.
|
| Előzmény: [671] kovátsnorbi1994, 2011-10-12 22:31:18 |
|
|
| [671] kovátsnorbi1994 | 2011-10-12 22:31:18 |
 Köszönöm a gyors választ és a javaslatokat jonas! A harmadiknál azt hiszem pont az integrálást nem tudtam elvégezni, szerintem kellett volna hozzá valamilyen azonos átalakítás, még azért megpróbálom és köszönöm még egyszer. A második feladatban én ott vesztettem el a fonalat, hogy a következő képpen értelmeztem a feladatot: A természetes sorrend gondolom a növekvő. Egy permutáció például a 6-5-1-4-3-2 mely eleget tesz a feltételnek, mert páronként összehasonlítva 3 esetben ugyanabban a sorrenben követik egymást a számok ahogy a számsorban is, vagyis jobb oldalon áll a nagyobb tőle balra pedig a kisebb, és ebben a permutációban pontosan 3 darab ilyen van. 65,61,64,63,62- 51,54,53,52- 14,13,12- 43,42- 32-
Itt tehát az 1 után 4, 1 után 3 végül az 1 után 2 is áll. De például az 1-2-3-4-5-6 esetén 15 db "természetes követés" van, míg mondjuk a 6-5-4-3-2-1-ben meg egy sincs. Viszont így azt hiszem nem találtam 63 darab helyes megoldást. Egyébként szerintem is elég ostobán van megfogalmazva ez a feladat.
|
| Előzmény: [670] jonas, 2011-10-12 21:25:06 |
|
| [670] jonas | 2011-10-12 21:25:06 |
 A 2. feladatot nem értem.
A 3. feladatnál először bizonyítsd be, hogy az x0 körül f értelmezett és folytonos. Utána használd a Newton-Leibniz tételt ahhoz, hogy meghatározd a primitív függvény deriváltját az x0 pontban.
A 4. feladatot talán többféleképpen is el lehet kezdeni. Én úgy kezdeném, hogy először azt szeretném belátni, hogy a=1. Ezt úgy látod be, hogy ha modnjuk a<1, akkor (a2x+b)/(2ax+b) határértéke az x  -ben nulla lenne, pedig mi azt szeretnénk, hogy ez a hányados minden x esetén pontosan 1 legyen. Hasonlót lehet mondani, ha 1<a lenne. -ben nulla lenne, pedig mi azt szeretnénk, hogy ez a hányados minden x esetén pontosan 1 legyen. Hasonlót lehet mondani, ha 1<a lenne.
|
| Előzmény: [669] kovátsnorbi1994, 2011-10-12 20:39:44 |
|
| [669] kovátsnorbi1994 | 2011-10-12 20:39:44 |
 Helló mindenki! Az egyik ismerősöm mutatott egy feladatsort (emelt érettségire készülök, gépész főisk. a terv), és kiválogattam belőle néhány feladatot amiket nem tudtam megoldani :-( Annak ellenére sem, hogy a feladatok végeredményét néhány esetben látom, de nem értem hogy jött ki! Felteszem: könnyű példákról van szó és én vagyok a béna valószínűleg, ezért is ebbe a témába írom. Összesen 2 kérdés-sorozatom van, most az elsőt írom le és ha jön rá válasz, leírom a másodikat is. Ahol megtaláltam a feladat forrást, leírtam, az eredménnyel együtt. Előre is köszi mindenkinek, aki részletes megoldással válaszol! Norbi
![1. \qquad a.) \lim_{n\to\infty}\left[{n\sin{\left(\frac1n\right)}}\right]^n=? \qquad b.) \lim_{x\to\pm\infty}\root{x}\of{\frac{\sin{x}}x}=? \qquad c.) \lim_{x\to0}\root{x}\of{\frac{\sin{x}}x}=?](keplet.cgi?k=CD67E9C72865D225)
2.) Állapítsa meg,hogy az 1,2,3,4,5,6 számoknak hány olyan különböző permutációja van. amelyben pontosan három szám a természetes sorrendben
követi egymást! Scharnitzky Viktor: Matematikai feladatok (a műszaki fősikolák számára) 158.oldal 11.3 feladat és a megoldás: 63.
3.) Határozzuk meg milyen irányúak az y = f(x) függvény primitív függvényeinek az érintői az x0 abszcisszájú pontban, ha

Sain Márton: Matematikai feladatgyűjtemény III. , 1987. 192. oldal 16.70. (3) részfeladat, melynek megoldása: Az érintők vízszintesek.
4.) Határozzuk meg mindazon a,b valós számokat, melyekre a 0 és minden valós x esetén: 0 és minden valós x esetén:
a . 2x+b = 2ax+b
Fazekas Mihály Gimnázium honlapján találtam itt.
|
|
| [668] Hajba Károly | 2011-10-04 21:31:18 |
 Ha a hurok mentén végighaladva nézzük, hogy hányszor fordulunk jobbra ill. balra, akkor az irányválasztástól függően az egyik 4-gyel több lesz, mint a másik. Azaz egy teljes fordulatot ír le (360°). Ha minden második fordulatot megjelöljük, akkor gyakorlatilag szétválasztottuk a vízszintesbe fordulást és a függőlegesbe fordulást. A hurok vonala nem metszi önmagát és teljesen kitölti a pályát.
Nézzük meg, hogy a lehetséges és lehetetlen esetek vonalvezetésénél milyen a vízszintes ágak irányultsága. A lehetségesnél mindkettő bemegy a csomópontba és ellenkező irányba megy ki. Az ellenkezője (egyik be, másik ki) nem lehetséges, mert ekkor a függőleges irányban is így kellene lennie és ha ezt a kettőt összekötöm, akkor az evvel kialakított hurokrészben lenne az egyik vízszintes és ezen kívül a másik vízszintes ág. Így azokat keresztezés nélkül nem lehetne összekötni.
Hasonló megfontoltságokból eredően a másik két esetben a vízszintes ágak egyike be, míg a másika ki mutat.
Azaz a lehetséges esetekben mindkét ág azonos kimenetirányultságú, mindkettő vagy függőlegesbe fordul vagy vízszintesbe A lehetetlen eseteknél a kimenő ágak mindig ellentétesek egymással.
S mivel a lehetséges esetek azonos irányultságúak, ezért vagy mindkettő jelölt vagy mindkettő jelöletlen.
|
| Előzmény: [653] Valezius, 2011-04-12 14:38:15 |
|
| [667] Kemény Legény | 2011-09-25 18:39:48 |
 Így már valóban jobbnak tűnik megoldásod. Ha állandóan a precíz feladatkitűzést követeled meg, akkor az a legkevesebb, hogy a megoldásaid is olyanok legyenek, amilyeneket magad is mgkövetelsz másoktól...
|
| Előzmény: [665] Róbert Gida, 2011-09-25 14:00:46 |
|
| [666] Róbert Gida | 2011-09-25 14:07:59 |
 További érdekes általánosítások: mi van akkor, ha v valószínűséggel születik sárkányfiú, és 1-v-vel sárkánylány? Vagy, ha egy évben több párzási ciklus van? A sárkánylányok r>0 valószínűséggel elvételnek? s>0 valószínűséggel meteor csapódik be, és kihalnak, mint a dinoszauruszok? u>0 valószínűséggel adott évben a hadjárat elmarad?
|
| Előzmény: [665] Róbert Gida, 2011-09-25 14:00:46 |
|
| [665] Róbert Gida | 2011-09-25 14:00:46 |
 Ügyes vagy, leülhetsz. Az azért látható, hogy csak néhány kisebb/nagyobb egyenlőt szúrtam el. Helyesen:
Ebben az esetben  esetében a kolónia fennmaradhat, míg esetében a kolónia fennmaradhat, míg 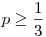 esetén biztosan kipusztul. Legyen először esetén biztosan kipusztul. Legyen először 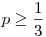 , ha legfeljebb , ha legfeljebb  sárkányfiú van, akkor első hadjárat során öljék meg őket, ekkor nem marad sárkányfiú, és a kolónia kihal. Így feltehető, hogy több, mint sárkányfiú van, akkor első hadjárat során öljék meg őket, ekkor nem marad sárkányfiú, és a kolónia kihal. Így feltehető, hogy több, mint  sárkányfiú van, ami azt jelenti, hogy kevesebb, mint sárkányfiú van, ami azt jelenti, hogy kevesebb, mint 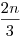 sárkánylány. Ekkor a hadjáratok során csak őket öljék meg: legyen kezdetben sárkánylány. Ekkor a hadjáratok során csak őket öljék meg: legyen kezdetben 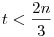 sárkánylány a kolóniában, ekkor egy hadjárat után számuk t-pn lesz (vagy nulla, ha ez negatív), míg a szülések után 2(t-pn)<t, így n év alatt kihalnak. sárkánylány a kolóniában, ekkor egy hadjárat után számuk t-pn lesz (vagy nulla, ha ez negatív), míg a szülések után 2(t-pn)<t, így n év alatt kihalnak.
Ellenkező irány: legyen  és és  sárkányfiú és sárkányfiú és 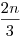 sárkánylány. Egy hadjárat alatt megölnek kevesebb, mint sárkánylány. Egy hadjárat alatt megölnek kevesebb, mint  sárkányt, így biztosan megmarad legalább sárkányt, így biztosan megmarad legalább  sárkánylány és legalább egy sárkányfiú. A szülésekkel pótolják a meghalt sárkányokat (annyi sárkánylány és fiú szülessen, mint amennyit megöltek), ekkor visszaáll az eredeti állapot, a maradék születések olyanok legyenek, hogy a kolóniában az 1:2 arány fennmaradjon a sárkányfiúk és lányok között (+-1 sárkány, ha n nem osztható 3-mal). Ekkor a kolónia nem hal ki, feltéve, hogy n elég nagy. Ezt csak Kemény Legénynek írom, mert igen, ha mondjuk p=0.3333, akkor bizony megeshet, hogy mondjuk az ezredik hadjárat után szépen kihalnak (ha a kezdeti n kicsi, és a +-1 sárkány éppen annyira megbillenti az 1:2 arányt, hogy nekünk rossz lesz). sárkánylány és legalább egy sárkányfiú. A szülésekkel pótolják a meghalt sárkányokat (annyi sárkánylány és fiú szülessen, mint amennyit megöltek), ekkor visszaáll az eredeti állapot, a maradék születések olyanok legyenek, hogy a kolóniában az 1:2 arány fennmaradjon a sárkányfiúk és lányok között (+-1 sárkány, ha n nem osztható 3-mal). Ekkor a kolónia nem hal ki, feltéve, hogy n elég nagy. Ezt csak Kemény Legénynek írom, mert igen, ha mondjuk p=0.3333, akkor bizony megeshet, hogy mondjuk az ezredik hadjárat után szépen kihalnak (ha a kezdeti n kicsi, és a +-1 sárkány éppen annyira megbillenti az 1:2 arányt, hogy nekünk rossz lesz).
|
| Előzmény: [664] Kemény Legény, 2011-09-25 11:36:54 |
|
| [664] Kemény Legény | 2011-09-25 11:36:54 |
 Tehát az ellenkező irányra adott megoldásod pl. az n=6, 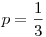 esetben: van 2 sárkányfiú+ 4 sárkánylány. Ha Artúr megöli mind a 2=n*p sárkányfiút, a lányok nehezen fognak utódokat nemzeni és pótolni a veszteségeket... esetben: van 2 sárkányfiú+ 4 sárkánylány. Ha Artúr megöli mind a 2=n*p sárkányfiút, a lányok nehezen fognak utódokat nemzeni és pótolni a veszteségeket...
|
| Előzmény: [663] Róbert Gida, 2011-09-25 09:40:53 |
|
| [663] Róbert Gida | 2011-09-25 09:40:53 |
 Ebben az esetben  esetében a kolónia fennmaradhat, míg esetében a kolónia fennmaradhat, míg 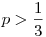 esetén biztosan kipusztul. Legyen először esetén biztosan kipusztul. Legyen először 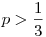 , ha legfeljebb , ha legfeljebb  sárkányfiú van, akkor első hadjárat során öljék meg őket, ekkor nem marad sárkányfiú, és a kolónia kihal. Így feltehető, hogy legalább sárkányfiú van, akkor első hadjárat során öljék meg őket, ekkor nem marad sárkányfiú, és a kolónia kihal. Így feltehető, hogy legalább  sárkányfiú van, ami azt jelenti, hogy legfeljebb sárkányfiú van, ami azt jelenti, hogy legfeljebb 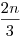 sárkánylány. Ekkor a hadjáratok során csak őket öljék meg: egy hadjárat után számuk kevesebb, mint sárkánylány. Ekkor a hadjáratok során csak őket öljék meg: egy hadjárat után számuk kevesebb, mint  lesz, míg a szülések után kevesebb, mint lesz, míg a szülések után kevesebb, mint  , így , így 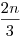 év alatt kihalnak. év alatt kihalnak.
Ellenkező irány: legyen  és és  sárkányfiú és sárkányfiú és 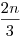 sárkánylány. Egy hadjárat alatt megölnek legfeljebb sárkánylány. Egy hadjárat alatt megölnek legfeljebb  sárkányt, így biztosan megmarad legalább sárkányt, így biztosan megmarad legalább  sárkánylány. A szülésekkel pótolják a meghalt sárkányokat (annyi sárkánylány és fiú szülessen, mint amennyit megöltek), ekkor visszaáll az eredeti állapot, a maradék születések olyanok legyenek, hogy a kolóniában az 1:2 arány fennmaradjon a sárkányfiúk és lányok között (+-1 sárkány, ha n nem osztható 3-mal). Ekkor a kolónia nem hal ki sárkánylány. A szülésekkel pótolják a meghalt sárkányokat (annyi sárkánylány és fiú szülessen, mint amennyit megöltek), ekkor visszaáll az eredeti állapot, a maradék születések olyanok legyenek, hogy a kolóniában az 1:2 arány fennmaradjon a sárkányfiúk és lányok között (+-1 sárkány, ha n nem osztható 3-mal). Ekkor a kolónia nem hal ki
|
| Előzmény: [662] Csimby, 2011-09-24 19:27:09 |
|
| [662] Csimby | 2011-09-24 19:27:09 |
 Ez jó, ha véletlenszerűen ölik a sárkányokat. De most engedjük meg, hogy válogathassanak is (valami külső jel alapján el tudják dönteni egy alvó sárkányról hogy hím vagy nőstény).
|
| Előzmény: [661] Róbert Gida, 2011-09-24 19:14:02 |
|











 -ben nulla lenne, pedig mi azt szeretnénk, hogy ez a hányados minden x esetén pontosan 1 legyen. Hasonlót lehet mondani, ha 1<a lenne.
-ben nulla lenne, pedig mi azt szeretnénk, hogy ez a hányados minden x esetén pontosan 1 legyen. Hasonlót lehet mondani, ha 1<a lenne.  0 és minden valós x esetén:
0 és minden valós x esetén: 
